Задания для контрольной работы. Рекомендации по выполнению и оформлению контрольных работ
Рекомендации по выполнению и оформлению контрольных работ
1. Прежде чем приступить к выполнению контрольного задания, следует изучить соответствующий теоретический материал по указанной литературе, выработать навыки решения типовых задач и примеров. При выполнении контрольной работы необходимо придерживаться следующих правил.
2. Контрольная работа должна быть выполнена студентом в отдельной ученической тетради в клетку с полями не менее 2 см для замечаний преподавателя.
3. На обложке тетради указываются фамилия, имя, отчествостудента, ШИФР (номер студенческого билета), курс, факультети специальность, по которой он обучается, номери вариантконтрольной работы.
4. Условия задач переписываются полностью, без сокращения слов, после чего приводится подробноерешение со ссылками на использованные при этом определения, теоремы, формулы; в конце решения записывается ответ; чертежи выполняются аккуратно, при помощи карандаша и линейки.
5. В работу должны быть включены все задания, указанные в контрольной работе. Работа, содержащая не все задания, а также задания не своего варианта, не засчитывается.
6. Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу на повторную проверку.
7.Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.
Контрольную работу необходимо сдать в деканат для проверки не позднее 25 мая. Контрольную работу студент после проверки предъявляет к защите. На защите студент должен, в случае необходимости, суметь объяснить свое решение, ответить на поставленные преподавателем вопросы по решению задачи. Без защищенных работ студент к сессии не допускается.
Для удобства студентов в институте организуются консультации.
Теоретические вопросы
Тема 1. Элементы теории множеств.Множества, отношения на множествах. Операции над множествами. Отображения и функции. Комбинаторика. Сочетания, размещения, перестановки. С повторением. Метод математической индукции.
Тема 2. Теория графов. Графы. Изоморфизм. Пути (критический) в графе. Циклы Эйлера, Гамильтона. Деревья. Числа в графах. Алгоритм Форда-Фалкерсона. Сети, транспортные сети.
Тема 3. Элементы математической логики. Истинные и ложные высказывания. Основные законы и свойства. Предикаты. Алгебра предикатов. Кванторы всеобщности и существования. Схемы логических рассуждений. Булевы функции. Совершенные нормальные формы. Полином Жегалкина. Релейно-контактные схемы.
Тема 4. Элементы теории алгоритмов.Алфавит, слово, язык. Классификация грамматик и языков. Конечные автоматы. Машина Тьюринга. Нечеткие множества. Нечеткие алгоритмы.
Литература
1.Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М; Новосибирск: НГТУ, 2003 (2009). – 280 с. – (Серия «Высшее образование»).
2.Яблонский С.В. Введение в дискретную математику: Учеб. пособие для вузов/ Под ред. В.А. Садовничего. – 3-е изд., стер. – М.:Высш.шк., 2002. – 384 с.
3.Белоусов А.И., Ткачев С.Б. Дискретная математика: Учеб. для вузов/ Под ред. Зарубина В.С., Крищенко А.П. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 744 с.
4.Бакеева Л.В. Переключательные функции: учебное пособие.– Казань: Изд-во Казан. гос. технол. ун-та, 2008. – 92 с.
5.Бакеева Л.В., Шемелова О.В. Элементы теории графов и некоторые ее приложения.– Нижнекамск: НХТИ (филиал) ФГБОУ ВПО «КНИТУ», 2014. – 53 с.
6.Гончарова Г. А., Мочалин А. А. Элементы дискретной математики: Учебное пособие. М.: ФФОРУМ: ИНФРА-М, 2003. – 128 с.
7.Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. – 304 с.:ил.
8.Москинова Г.И. Дискретная математика: учебное пособие. – М.:Логос, 2000. – 240 с.: ил.
Выбор задач своего варианта осуществляется в соответствии с таблицей.
| Варианты | Номера заданий | ||||||||||||
| 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | 7.7 | 8.8 | 9.9 | 10.10 | 11.1 | 12.2 | 13.3 | |
| 1.2 | 2.3 | 3.4 | 4.5 | 5.6 | 6.7 | 7.8 | 8.9 | 9.10 | 10.1 | 11.2 | 12.3 | 13.4 | |
| 1.3 | 2.4 | 3.5 | 4.6 | 5.7 | 6.8 | 7.9 | 8.10 | 9.1 | 10.2 | 11.3 | 12.4 | 13.5 | |
| 1.4 | 2.5 | 3.6 | 4.7 | 5.8 | 6.9 | 7.10 | 8.1 | 9.2 | 10.3 | 11.4 | 12.5 | 13.6 | |
| 1.5 | 2.6 | 3.7 | 4.8 | 5.9 | 6.10 | 7.1 | 8.2 | 9.3 | 10.4 | 11.5 | 12.6 | 13.7 | |
| 1.6 | 2.7 | 3.8 | 4.9 | 5.10 | 6.1 | 7.2 | 8.3 | 9.4 | 10.5 | 11.6 | 12.7 | 13.8 | |
| 1.7 | 2.8 | 3.9 | 4.10 | 5.1 | 6.2 | 7.3 | 8.4 | 9.5 | 10.6 | 11.7 | 12.8 | 13.9 | |
| 1.8 | 2.9 | 3.10 | 4.1 | 5.2 | 6.3 | 7.4 | 8.5 | 9.6 | 10.7 | 11.8 | 12.9 | 13.10 | |
| 1.9 | 2.10 | 3.1 | 4.2 | 5.3 | 6.4 | 7.5 | 8.6 | 9.7 | 10.8 | 11.9 | 12.10 | 13.1 | |
| 1.10 | 2.1 | 3.2 | 4.3 | 5.4 | 6.5 | 7.6 | 8.7 | 9.8 | 10.9 | 11.10 | 12.1 | 13.2 | |
| 1.1 | 2.3 | 3.5 | 4.4 | 5.6 | 6.7 | 7.8 | 8.8 | 9.10 | 10.10 | 11.2 | 12.4 | 13.3 | |
| 1.2 | 2.4 | 3.6 | 4.5 | 5.7 | 6.8 | 7.10 | 8.9 | 9.1 | 10.1 | 11.3 | 12.5 | 13.5 | |
| 1.3 | 2.5 | 3.7 | 4.6 | 5.8 | 6.9 | 7.1 | 8.10 | 9.2 | 10.2 | 11.4 | 12.6 | 13.6 | |
| 1.4 | 2.6 | 3.8 | 4.7 | 5.9 | 6.10 | 7.2 | 8.1 | 9.3 | 10.3 | 11.5 | 12.7 | 13.7 | |
| 1.5 | 2.7 | 3.9 | 4.8 | 5.10 | 6.1 | 7.3 | 8.2 | 9.4 | 10.4 | 11.6 | 12.8 | 13.8 | |
| 1.6 | 2.8 | 3.10 | 4.9 | 5.1 | 6.2 | 7.4 | 8.3 | 9.5 | 10.5 | 11.7 | 12.9 | 13.9 | |
| 1.7 | 2.9 | 3.1 | 4.10 | 5.2 | 6.3 | 7.5 | 8.5 | 9.6 | 10.6 | 11.8 | 12.10 | 13.10 | |
| 1.8 | 2.10 | 3.2 | 4.1 | 5.3 | 6.4 | 7.6 | 8.6 | 9.7 | 10.7 | 11.9 | 12.1 | 13.1 | |
| 1.9 | 2.1 | 3.3 | 4.2 | 5.4 | 6.5 | 7.7 | 8.7 | 9.8 | 10.8 | 11.10 | 12.2 | 13.2 | |
| 1.10 | 2.2 | 3.4 | 4.3 | 5.5 | 6.8 | 7.8 | 8.8 | 9.1 | 10.9 | 11.1 | 12.3 | 13.3 | |
| 1.1 | 2.4 | 3.7 | 4.4 | 5.7 | 6.9 | 7.9 | 8.9 | 9.2 | 10.10 | 11.2 | 12.5 | 13.4 | |
| 1.2 | 2.5 | 3.8 | 4.5 | 5.8 | 6.10 | 7.10 | 8.10 | 9.3 | 10.1 | 11.4 | 12.6 | 13.5 | |
| 1.3 | 2.6 | 3.9 | 4.6 | 5.9 | 6.1 | 7.1 | 8.1 | 9.4 | 10.2 | 11.5 | 12.7 | 13.6 | |
| 1.4 | 2.7 | 3.10 | 4.7 | 5.10 | 6.2 | 7.2 | 8.2 | 9.5 | 10.3 | 11.6 | 12.8 | 13.7 | |
| 1.5 | 2.8 | 3.1 | 4.8 | 5.1 | 6.3 | 7.3 | 8.3 | 9.6 | 10.4 | 11.7 | 12.9 | 13.8 | |
| 1.6 | 2.9 | 3.2 | 4.9 | 5.2 | 6.4 | 7.4 | 8.4 | 9.7 | 10.5 | 11.8 | 12.10 | 13.9 | |
| 1.7 | 2.10 | 3.3 | 4.10 | 5.3 | 6.5 | 7.5 | 8.5 | 9.8 | 10.6 | 11.9 | 12.1 | 13.10 | |
| 1.8 | 2.1 | 3.4 | 4.1 | 5.4 | 6.6 | 7.6 | 8.6 | 9.9 | 10.7 | 11.10 | 12.2 | 13.1 | |
| 1.9 | 2.2 | 3.5 | 4.2 | 5.5 | 6.9 | 7.8 | 8.7 | 9.10 | 10.8 | 11.1 | 12.4 | 13.3 | |
| 1.10 | 2.3 | 3.6 | 4.3 | 5.8 | 6.10 | 7.9 | 8.8 | 9.2 | 10.9 | 11.2 | 12.6 | 13.8 |
По возникшим вопросам можно обратиться по e-mail: [email protected] (указывать номер группы, предмет и ФИО)
Задания для контрольной работы
Задание № 1.
Дано множество 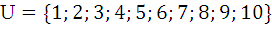 и множества A, B, и С. Записать множества и построить результаты на диаграммах Эйлера-Венна:
и множества A, B, и С. Записать множества и построить результаты на диаграммах Эйлера-Венна:
1). 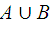 | 2). 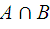 | 3).  |
4).  | 5). 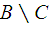 | 6). 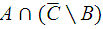 . . |
1.1. 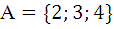 ,
, 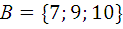 ,
, 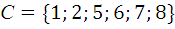 .
.
1.2.  ,
, 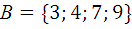 ,
,  .
.
1.3. 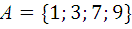 ,
, 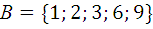 ,
, 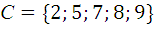 .
.
1.4.  ,
, 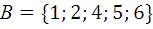 ,
, 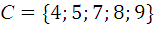 .
.
1.5.  ,
,  ,
, 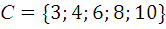 .
.
1.6. 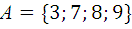 ,
,  ,
,  .
.
1.7.  ,
, 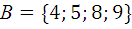 ,
,  .
.
1.8.  ,
, 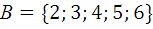 ,
, 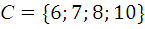 .
.
1.9. 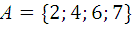 ,
, 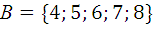 ,
, 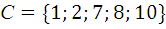 .
.
1.10. 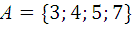 ,
,  ,
,  .
.
Задание № 2.
Используя операции над множествами, описать заштрихованную область.
2.1.
| 2.2.
| 2.3.
| ||||||||||||
2.4.
| 2.5.
| 2.6.
| ||||||||||||
2.7.
| 2.8.
| 2.9.
| ||||||||||||
2.10.
|
Задание № 3.
Даны множества Х и У. Найти множества:
1) 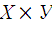 | 2) 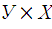 | 3)  . . |
3.1. 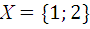 и
и  .
.
3.2. 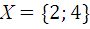 и
и  .
.
3.3. 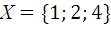 и
и 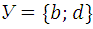 .
.
3.4.  и
и 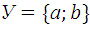 .
.
3.5. 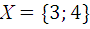 и
и  .
.
3.6.  и
и  .
.
3.7.  и
и  .
.
3.8.  и
и 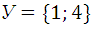 .
.
3.9.  и
и 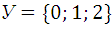 .
.
3.10. 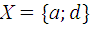 и
и  .
.
Задание № 4.
Дано множество М. Задать списком и матрицей отношение  , указать свойства отношения (рефлексивность, антирефлексивность, симметричность, антисимметричность и транзитивность). Ответы обосновать.
, указать свойства отношения (рефлексивность, антирефлексивность, симметричность, антисимметричность и транзитивность). Ответы обосновать.
4.1.  , R – быть больше.
, R – быть больше.
4.2. 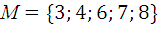 , R – быть меньше.
, R – быть меньше.
4.3.  , R – давать разность равную 2.
, R – давать разность равную 2.
4.4. 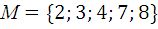 , R – быть не больше.
, R – быть не больше.
4.5.  , R – давать положительную разность.
, R – давать положительную разность.
4.6. 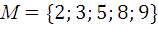 , R – быть делителем.
, R – быть делителем.
4.7. 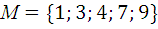 , R – в сумме давать 10.
, R – в сумме давать 10.
4.8. 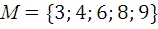 , R – иметь общий делитель, отличный от единицы.
, R – иметь общий делитель, отличный от единицы.
4.9.  , R – быть больше на 1.
, R – быть больше на 1.
4.10.  , R – давать произведение больше 7.
, R – давать произведение больше 7.
Задание № 5.
На множестве 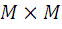 задано отношение R. Указать свойства отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность и транзитивность). Ответы обосновать.
задано отношение R. Указать свойства отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность и транзитивность). Ответы обосновать.
5.1. М – множество сотрудников фирмы, R – быть начальником.
5.2. М – множество сотрудников фирмы, R – быть непосредственным начальником.
5.3. М – множество студентов учебного заведения, R – учатся в одной группе.
5.4. М – множество людей, R – жить в одном городе.
5.5. М – множество людей, R – быть одного пола.
5.6. М – множество мужчин, R – быть отцом.
5.7. М – множество мужчин, R – быть братом.
5.8. М – множество мужчин, R – быть сыном.
5.9. М – множество людей, R – быть одного роста.
5.10. М – множество людей, R – быть выше (рост).
Задание № 6.
Даны отношения R1 и R2. Найти:
1)  2)
2)  3)
3) 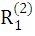 4)
4) 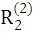 5)
5)  6)
6) 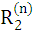
6.1. 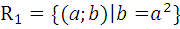
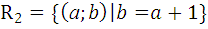 .
.
6.2. 
 .
.
6.3. 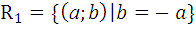
 .
.
6.4. 
 .
.
6.5. 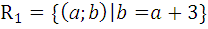
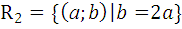 .
.
6.6. 
 .
.
6.7. 
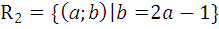 .
.
6.8. 
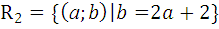 .
.
6.9. 
 .
.
6.10. 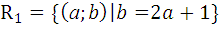
 .
.
Задание № 7.
7.1. Колода карт из 36 карт. Сколькими способами можно достать 5 карт так, чтобы среди них были пиковые карты?
7.2. Колода карт из 36 карт. Сколькими способами можно достать 5 карт так, чтобы среди них были три пиковые и одна червовая карты?
7.3. На заводе 10 специалистов с высшим образованием и 15 – со средне-специальным. Сколькими способами можно сформировать бригаду из 5 человек, в которой было бы не более двух человек с высшим образованием?
7.4. В хирургическом отделении 8 врачей и 25 мед. сестер. Сколькими способами можно составить бригаду из 2 врачей и 5 мед. сестер?
7.5. Имеется десять различных цветков. Нужно составить из них букеты (количество цветков в букете нечетное). Сколькими способами это можно сделать?
7.6. Группа студентов состоит из 10 девушек и 12 юношей. Сколькими способами можно составить группу из 6 человек для участия в конференции так, чтобы среди них было не более двух девушек?
7.7. Группа студентов состоит из 7 девушек и 10 юношей. Сколькими способами можно составить группу из 5 человек для участия в спартакиаде так, чтобы среди них было не менее двух девушек?
7.8. В фирме работают 12 специалистов с высшим образованием и 20 – со средне-специальным. Сколькими способами можно сформировать командировочную группу из 5 человек, в которой было бы не менее двух человек с высшим образованием?
7.9. Колода из 52 карт. Сколькими способами можно достать 7 карт так, чтобы среди них были две пиковые карты и три бубновые?
7.10. Колода из 52 карт. Сколькими способами можно достать 5 карт так, чтобы среди них были карты всех четырех мастей?
Задание № 8.
8.1. Сколько различных трехзначных чисел можно составить из цифр 0, 2, 3, 5, 7 если: цифры не повторяются?
8.2. Сколько трехзначных чисел, делящихся на 2, можно составить из цифр 0, 2, 3, 6 и 7, если каждое число не содержит одинаковых цифр?
8.3. Автомобильный номер содержит четыре цифры. Сколько номеров содержат цифру 7?
8.4. Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 2, 3, 5 и 6, если число может содержать одинаковые цифры?
8.5. Кодовый замок содержит 4 цифры. Сколько существует различных комбинаций содержащих цифры 2?
8.6. Группа шахматистов сыграла между собой 28 партий. Каждые два из них встречались между собой один раз. Сколько шахматистов участвовало в соревновании?
8.7. Сколько различных «слов» (под «словом» понимается любая комбинация букв) можно составить, переставляя буквы в слове «АГА»? «MISSISIPPI»?
8.8. Сколько различных «слов» (под «словом» понимается любая комбинация букв) можно составить, переставляя буквы в слове «МАМА»? «АНАНАС»?
8.9. Сколькими возможными способами 3 человека могут разместиться в 8 вагонах электрички?
8.10. Сколько прямых линий можно провести через 7 точек, из которых лишь 3 лежат на одной прямой?
Задание № 9.
Решить комбинаторное уравнение (систему уравнений).
9.1. 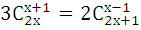 | 9.2. 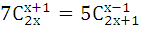 |
9.3. 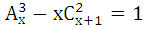 | 9.4. 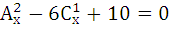 |
9.5.  | 9.6.r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  |
9.7. 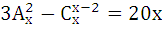 | 9.8. 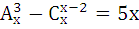 |
9.9. 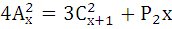 | 9.10.  |
Задание № 10.
Для функции 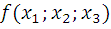
а) вычислить значения на наборах (1;0;0) и (0;1;0);
б) найти СДНФ (совершенную дизъюнктивную нормальную форму);
в) найти СКНФ (совершенную конъюнктивную нормальную форму).
Пункты б) и в) выполнить двумя способами: применяя таблицу истинности и используя основные законы и свойства.
10.1. 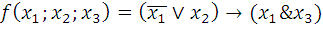
10.2. 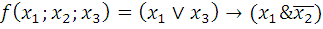
10.3. 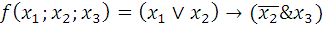
10.4. 
10.5. 
10.6. 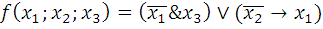
10.7. 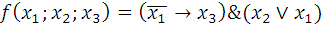
10.8. 
10.9. 
10.10. 
Задание № 11.
Представить функцию 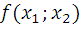 в виде полинома Жегалкина.
в виде полинома Жегалкина.
11.1. 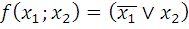
11.2. 
11.3. 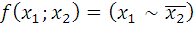
11.4. 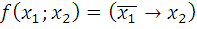
11.5. 
11.6. 
11.7. 
11.8. 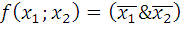
11.9. 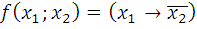
11.10.  .
.
Задание № 12.
Рассмотреть все варианты квантификации предикатов и определить истинность полученных высказываний.
12.1. 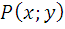 – «х учится в одной группе с у»
– «х учится в одной группе с у»
12.2. 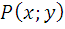 – «х живет в одном доме с у»
– «х живет в одном доме с у»
12.3. 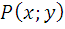 – «х брат для у»
– «х брат для у»
12.4. 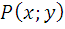 – «х работает в одной фирме с у»
– «х работает в одной фирме с у»
12.5. 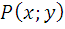 – «х является начальником у»
– «х является начальником у»
12.6. 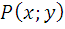 – «х является родственником у»
– «х является родственником у»
12.7. 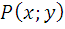 – «х старше у»
– «х старше у»
12.8. 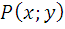 – «х является отцом у»
– «х является отцом у»
12.9. 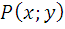 – «х моложе у»
– «х моложе у»
12.10. 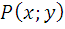 – «х живет в одном городе с у».
– «х живет в одном городе с у».
Задание № 13.
Задать изображенный граф
а) списком ребер;
б) матрицей смежности;
в) матрицей инцидентности;
г) списком смежности.
13.1.
| 13.2.
| ||||||||||||
13.3.
| 13.4.
| ||||||||||||
13.5.
| 13.6.
| ||||||||||||
13.7.
| 13.8.
| ||||||||||||
13.9.
| 13.10.
|
