Шардың (сфераның) кескінін салу

Мектеп геометриясындағы айналу денелері кескіндерінің ішіндегі ең күрделісі шардың кескінін салу болып табылады. Шарды кескіндеу барысында негізгі жазықтық ретінде, экватор деп аталатын үлкен дөңгелектердің бірі жатқан жазықтық қарастырылады. Экватордан ең алыс қашықтықта жатқан шар бетінің нүктелері, яғни экватор жазықтығына перпендикуляр диаметр ұштары – полюстар деп аталады. Сфераға тиісті және полюстар арқылы өтетін шеңберлер – меридиандар деп аталады. Осы сияқты география ұғымына сәйкес параллельдер ұғымын да енгізуге болады.

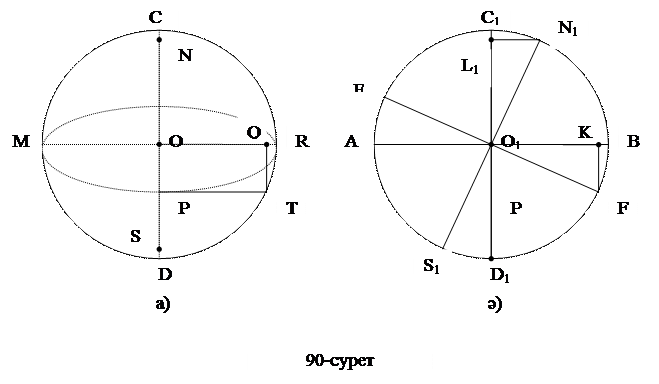
Шарды (сфераны) проекциялау барысында оның экваторының кескіні бейнелеу жазықтығында эллипс түрінде кескінделеді. Бұл эллипстің үлкен осі MR шардың кескінінің шекарасын беретін шеңбердің диаметрі болады. Шар полюстары бұл шеңбердің бойында жата алмайды. Егер жататын болса, онда шар бейнелеу жазықтығына параллель проекцияланып, оның экваторының кескіні эллипс емес MR кесіндісі болған болар еді. Өкінішке орай көп әдебиеттердің өзінде осындай қателер кездеседі. Шар экваторының кескіні эллипс болып кескінделуі үшін проекцияның ортогональдығын сақтай отырып, бейнелеу жазықтығына перпендикуляр жазықтықта шар осін кішкене бір бұрышқа бұру қажет. Сонда шар полюстарының кескіндері шеңбердің CD диаметрінің бойындағы N, S нүктелеріне жылжиды және ON=OS шарты орындалады (90,а-сурет).

Мұндағы экватордың кескіні болатын эллипстің үлкен жарты осі шар радиусына тең, ал кіші жарты ОР осінің ұзындығы ON=OS арақашықтығына тікелей байланысты. Осы байланысты анықтау үшін шардың осін айналдырған жазықтықпен қиғандағы қимасын аламыз (90,ә-сурет). Бұл суреттегі C₁D₁ – шар осінің бастапқы қалпы, N₁S₁ – остің бұрғаннан кейінгі қалпы. АВ – кесіндісі MR диаметріне перпендикуляр диаметрдің бастапқы қалпы болса, ЕҒ – осы диаметрдің бұрғаннан кейінгі қалпы. O₁L₁ - O₁N₁ кесіндісінің C₁D₁ түсірілген проекциясы; O₁K - O₁F кесіндісінің AB диаметріне түсірілген проекциясы; O₁L₁=ON болады, ал KF кесіндісі экваторды кескіндейтін эллипстің кіші жарты осінің шамасын береді. Сонымен қатар, L₁O₁N₁ және O₁KF үшбұрыштарының теңдігінен O₁L₁=O₁K екендігі шығады. Олай болса, шардың ортогональ проекциясынан алынған элементтер бойынша оның кескінін салудың мынадай қарапайым тәсілін аламыз.

1. Шардың шекарасының кескінін беретін центрі О және диаметрі CD болатын шеңбер салынады;

2. CD диаметрінің бойынан ON=OS болатындай, N және S нүктелері салынады;

3. CD диаметріне перпендикуляр MR диаметрі салынады;

4. MR диаметрінде OQ=ON кесіндісі өлшеп салынады;

5. Q нүктесінен MR диаметріне перпендикуляр түзу түсіріп, оның шеңбермен қиылысу нүктесін Т арқылы белгілеу;

6. QТ кесіндісінің шамасын кіші жарты осі етіп алып экватор кескінін беретін эллипсті салу.

Немесе керісінше, бірінші экватор кескінін кез келген эллипс етіп салып, одан кейін барып полюстарының кескіндерін салуға болады.

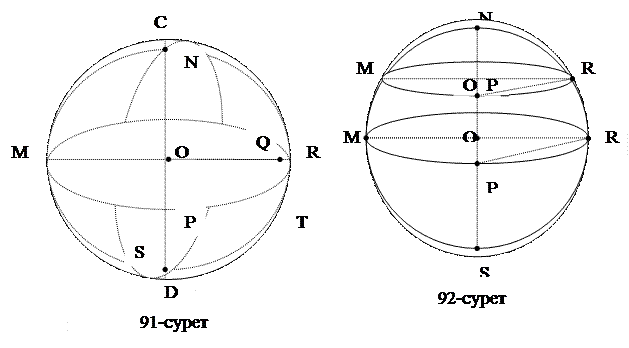
13-есеп: Шардың меридианын кескіндеу. Эллипстің өзара түйіндес диаметрлерін құрайтын NS және АВ арқылы эллипс жүргіземіз. Осыған ұқсас M, N, R және S нүктелері арқылы мередианның кескіні болатын эллипстің кескінін салуға болады (91-сурет).

14-есеп: Шардың ендіктерін кескіндеу. Ол үшін алдымен шардың MR диаметрінің ұштары және N, S полюстары арқылы өтетін мередианының кескінін салып аламыз. Шар ендіктері оның экваторы жазықтығымен параллель жазықтықтарда жататындығын және олар ұқсас эллипстер болатындығын ескерсек, NS диаметрін О₁ нүктесінде қиып өтетін ендіктің кескінін мынадай ретте салуға болады (92-сурет).

О₁ нүктесі арқылы шардың MR диаметріне параллель түзу жүргізіп, оның мередианмен қиылысу нүктелерін сәйкесінше M₁, R₁ нүктелері арқылы белгілейміз. R₁ нүктесінен РR кесіндісіне параллель түзу жүргізіп, оның NS диаметрімен қиылысу нүктесін Р₁ арқылы белгілейміз. Олай болса ізделінді ендіктің кескіні осы М₁, Р₁ және R₁ нүктелері арқылы өтетін эллипс болады.