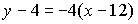Норма вектора в евклидовом пространстве
1. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 169
b) – 13
c) 13
d) 17
2. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 225
b) 15
c) – 15
d) 25
3. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 225
b) – 15
c) 15
d) 21
4. Норма вектора 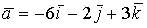 в пространстве
в пространстве  равна …
равна …
a) – 7
b) 49
c) 7
d) 11
5. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 169
b) –13
c) 13
d) 19
6. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 15
b) 225
c) – 15
d) 1
7. Норма вектора 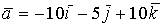 в пространстве
в пространстве  равна …
равна …
a) 225
b) 15
c) – 15
d) 25
8. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) – 15
b) 21
c) 225
d) 15
9. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 11
b) 49
c) 7
d) – 7
10. Норма вектора  в пространстве
в пространстве  равна …
равна …
a) 15
b) 23
c) 225
d) – 15
Область определения функции_ геометрическая интерпретация
1. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 
d) 
2. Областью определения функции 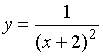 является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 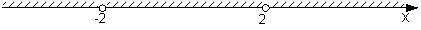
b) 
c) 
d) 
3. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 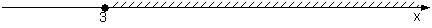
d) 
4. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 
d) 
5. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 
d) 
6. Областью определения функции 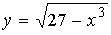 является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 
d) 
7. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 
d) 
8. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 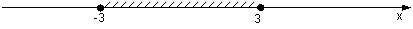
b) 
c) 
d) 
9. Областью определения функции 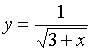 является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 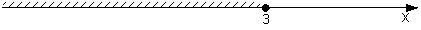
d) 
10. Областью определения функции  является промежуток, изображенный на числовой прямой…
является промежуток, изображенный на числовой прямой…
a) 
b) 
c) 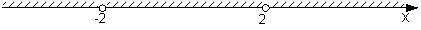
d) 
Обратная матрица
1. Матрица 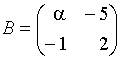 будет обратной к матрице
будет обратной к матрице  при
при  равном …
равном …
a) 15
b) 2
c) – 3
d) 3
2. Матрица  будет обратной к матрице
будет обратной к матрице  при
при  равном …
равном …
a) 2
b) 1
c) 6
d) – 2
3. Матрица  будет обратной к матрице
будет обратной к матрице 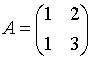 при
при  равном …
равном …
a) 6
b) 3
c) 1
d) – 3
4. Матрица  будет обратной к матрице
будет обратной к матрице  при
при  равном …
равном …
a) 8
b) 2
c) 1
d) – 1
5. Матрица  будет обратной к матрице
будет обратной к матрице 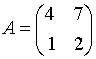 при
при  равном …
равном …
a) 14
b) 2
c) – 2
d) 8
6. Матрица  будет обратной к матрице
будет обратной к матрице 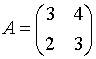 при
при  равном …
равном …
a) 3
b) – 3
c) 12
d) 7
7. Матрица  будет обратной к матрице
будет обратной к матрице 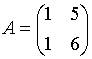 при
при  равном …
равном …
a) 4
b) 6
c) – 6
d) 30
8. Матрица  будет обратной к матрице
будет обратной к матрице 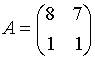 при
при  равном …
равном …
a) 7
b) 1
c) 6
d) – 1
9. Матрица  будет обратной к матрице
будет обратной к матрице 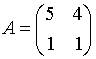 при
при  равном …
равном …
a) – 1
b) 1
c) 3
d) 4
10. Матрица 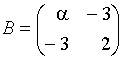 будет обратной к матрице
будет обратной к матрице 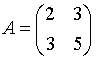 при
при  равном …
равном …
a) 4
b) – 5
c) 15
d) 5
Обратная матрица. Условие существования
1. Матрица  не имеетобратной при
не имеетобратной при  равном…
равном…
a) 12
b) 3
c) 2,4
d) -2,4
2. Матрица  не имеетобратной при
не имеетобратной при  равном…
равном…
a) 4
b) -8
c) 2
d) 8
3. Матрица 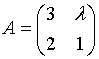 не имеетобратной при
не имеетобратной при  равном…
равном…
a) 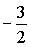
b) 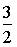
c) 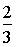
d) 2
4. Матрица 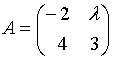 не имеетобратной при
не имеетобратной при  равном…
равном…
a) 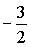
b) 4
c) 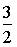
d) 6
5. Матрица 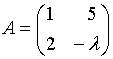 не имеетобратной при
не имеетобратной при  равном…
равном…
a) 10
b) 1
c) 5
d) -10
6. Матрица 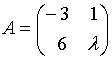 не имеетобратной при
не имеетобратной при  равном…
равном…
a) 1
b) -6
c) -2
d) 2
7. Матрица 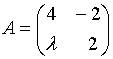 не имеетобратной при
не имеетобратной при  равном…
равном…
a) -8
b) 4
c) 2
d) -4
8. Матрица  не имеетобратной при
не имеетобратной при  равном
равном
a) 4
b) -2
c) 2
d) 1
9. Матрица 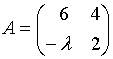 не имеетобратной при
не имеетобратной при  равном…
равном…
a) -3
b) 3
c) 2
d) -4
10. Матрица 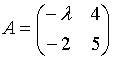 не имеетобратной при
не имеетобратной при  равном…
равном…
a) 1,6
b) -1,6
c) 8
d) 5
Общее уравнение плоскости
1. Нормальный вектор плоскости 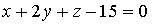 имеет координаты…
имеет координаты…
a) (1; 1; – 15)
b) (1; 2; 1)
c) (2; 1; – 15)
d) (1; 2; – 15)
2. Нормальный вектор плоскости 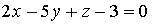 имеет координаты…
имеет координаты…
a) (2; – 5; – 1)
b) (– 5; 1; – 3)
c) (2; – 5; 1)
d) (2; – 5; – 3)
3. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (7; 0; – 1)
b) (7; 0; 0)
c) (7; – 1; – 1)
d) (– 7; 1; 1)
4. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (1; 1; – 1)
b) (– 1; 1; – 1)
c) (1; 1; 1)
d) (– 1; – 1; – 1)
5. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (– 2; – 2; – 5)
b) (– 2; – 2; – 2)
c) (2; 2; 2)
d) (2; 2; – 5)
6. Нормальный вектор плоскости 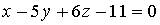 имеет координаты…
имеет координаты…
a) (– 5; 6; – 11)
b) (– 1; 5; – 6)
c) (1; – 5; 6)
d) (1; 6; – 11)
7. Нормальный вектор плоскости 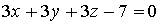 имеет координаты…
имеет координаты…
a) (– 3; – 3; – 7)
b) (3; 3; 3)
c) (3; 3; – 7)
d) (– 3; – 3; – 3)
8. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (2; – 1; 7)
b) (– 2; 1; – 7)
c) (2; 7; – 15)
d) (– 1; 7; – 15)
9. Нормальный вектор плоскости 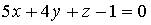 имеет координаты…
имеет координаты…
a) (5; 4; 1)
b) (– 5; – 4; – 1)
c) (5; 1; – 1)
d) (4; 1; – 1)
10. Нормальный вектор плоскости 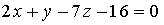 имеет координаты…
имеет координаты…
a) (1; – 7; – 16)
b) (– 2; – 1; 7)
c) (2; 1; – 7)
d) (2; – 7; – 16)
11. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (– 1; 1; 1)
b) (1; – 1; – 1)
c) (1; 1; 1)
d) (– 1; – 1; – 1)
12. Нормальный вектор плоскости 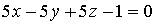 имеет координаты…
имеет координаты…
a) (5; 5; – 1)
b) (5; – 5; 5)
c) (– 5; 5; – 1)
d) (– 5; 5; – 5)
13. Нормальный вектор плоскости 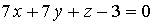 имеет координаты…
имеет координаты…
a) (– 7; – 1; – 3)
b) (7; 7; 1)
c) (7; 1; – 3)
d) (– 7; – 7; – 1)
14. Нормальный вектор плоскости 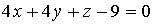 имеет координаты…
имеет координаты…
a) (4; 4; 1)
b) (4; 1; – 9)
c) (4; 4; – 9)
d) (– 4; – 4; – 1)
15. Нормальный вектор плоскости 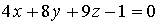 имеет координаты…
имеет координаты…
a) (4; 8; – 1)
b) (8; 9; – 1)
c) (4; 8; 9)
d) (– 4; – 8; – 9)
16. Нормальный вектор плоскости 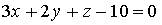 имеет координаты…
имеет координаты…
a) (2; 1; – 10)
b) (3; 1; – 10)
c) (3; 2; 1)
d) (– 3; – 2; – 1)
17. Нормальный вектор плоскости 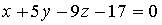 имеет координаты…
имеет координаты…
a) (– 1; – 5; 9)
b) (1; – 9; – 17)
c) (1; 5; – 9)
d) (5; – 9; – 17)
18. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (1; 1; – 13)
b) (1; – 13; 0)
c) (– 1; – 1; 13)
d) (– 1; – 1; 0)
19. Нормальный вектор плоскости  имеет координаты…
имеет координаты…
a) (1; 11; 1)
b) (– 1; – 11; – 1)
c) (1; – 1; – 11)
d) (– 1; 1; 11)
Общее уравнение прямой
1. Общим уравнением прямой на плоскости является …
a) 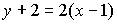
b) 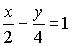
c) 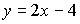
d) 
2. Общим уравнением прямой на плоскости является …
a) 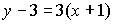
b) 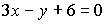
c) 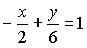
d) 
3. Общим уравнением прямой на плоскости является …
a) 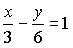
b) 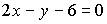
c) 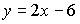
d) 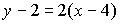
4. Общим уравнением прямой на плоскости является …
a) 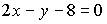
b) 
c) 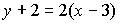
d) 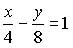
5. Общим уравнением прямой на плоскости является …
a) 
b) 
c) 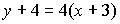
d) 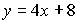
6. Общим уравнением прямой на плоскости является …
a) 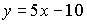
b) 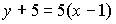
c) 
d) 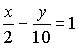
7. Общим уравнением прямой на плоскости является …
a) 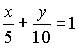
b) 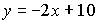
c) 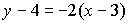
d) 
8. Общим уравнением прямой на плоскости является …
a) 
b) 
c) 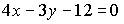
d) 
9. Общим уравнением прямой на плоскости является …
a) 
b) 
c) 
d) 
10. Общим уравнением прямой на плоскости является …
a) 
b) 
c) 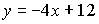
d)