Линейные однородные дифференциальные уравнения с

произвольными коэффициентами.

Рассмотрим уравнение вида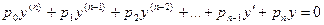

Определение. Выражение называется линейным дифференциальным оператором.

Линейный дифференциальный оператор обладает следующими свойствами:

1)

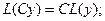
2)

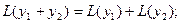
Решения линейного однородного уравнения обладают следующими свойствами:

1) Если функция у₁ является решением уравнения, то функция Су₁, где С – постоянное число, также является его решением.

2) Если функции у₁ и у₂ являются решениями уравнения, то у₁ +у₂ также является его решением.

Структура общего решения.

Определение. Фундаментальной системой решенийлинейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения.

Определение. Если из функций y_i составить определитель n – го порядка

,

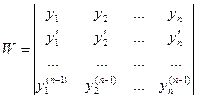то этот определитель называется определителем Вронского.

( Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик)

Теорема. Если функции 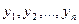линейно зависимы, то составленный для них определитель Вронского равен нулю.

Теорема. Если функции 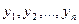линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.

Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения 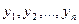была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.

Теорема. Если 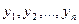- фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.

,

где C_i –постоянные коэффициенты.

Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.