Лабораторная работа №2 Действия с матрицами в MathCad
Цель работы:выполнение действий с матрицами в программе MathCad .
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad .
2. Создать матрицы 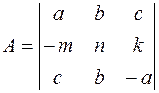 ,
,  ,
,  ,
,  ,
, 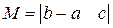 ,
,  из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 |
Пример
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:
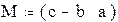
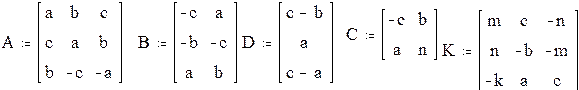
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).

Рисунок 21 - Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А - (3´3), В - (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A2; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) .
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).
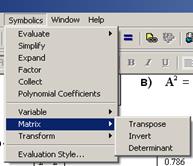
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде
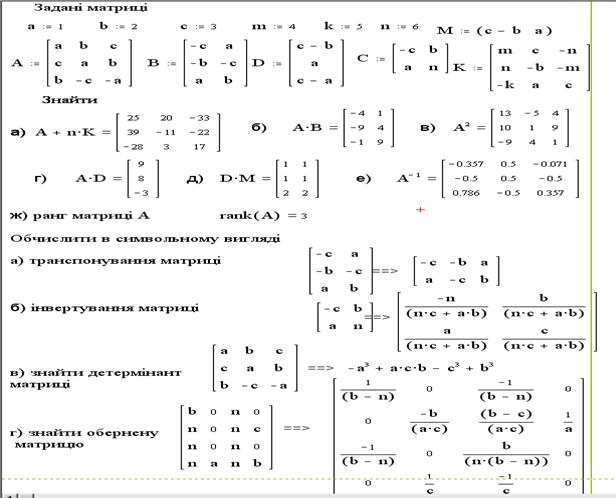
Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
