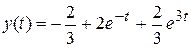П.4. Нахождение оригиналов с помощью теоремы запаздывания.

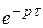Если изображение имеет вид рациональной дроби, умноженной на , где 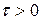, то сначала надо найти оригинал от рациональной дроби, а затем применить теорему запаздывания.

Пример1. Найти оригинал следующего изображения: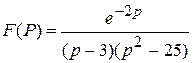

Найдем сначала оригинал для дроби .

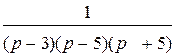Разложим эту дробь на простейшие и найдем коэффициенты методом неопределенных коэффициентов

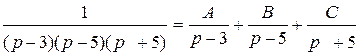
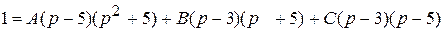
При 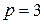получим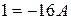

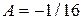
При 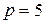получим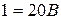

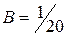
При 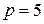получим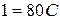

,

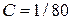
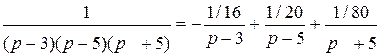оригинал равен 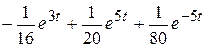, а оригинал данного .

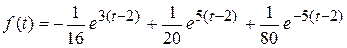Примеры для самостоятельного решения.
Найти оригиналы следующих изображений:

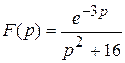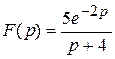1) ; 2) ; 3) ;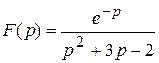

4)

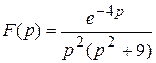
Ответы:

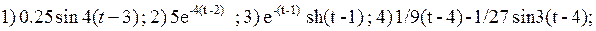
Применение операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами.

Принцип решения рассмотрим на примере решения уравнения второго порядка. Пусть требуется решить задачу Коши:

.

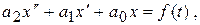
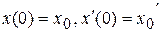Пусть 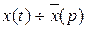, а f(t) 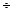F(p), тогда ,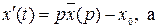

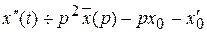Применим к обеим частям этого уравнения преобразование Лапласа, уравнение примет вид:

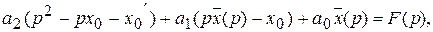или .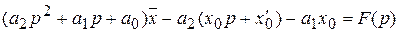

Это уравнение является алгебраическим, линейным относительно 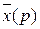. Решив его, получим .

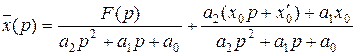Теперь по найденному изображению 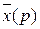можно восстановить соответствующий ему оригинал x(t),т.е. найти решение данного дифференциального уравнения. Легко заметить, что в знаменателях обеих дробей стоит характеристический многочлен исходного уравнения, и что простой вид 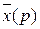приобретает, если начальные условия задачи Коши нулевые.

Пример 1. Решить задачу Коши .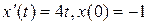

Решение.

Обозначим через 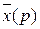изображение искомого решения, тогд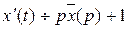а , а 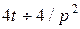, а изображение данного уравнения имеет вид 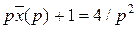, откуда .

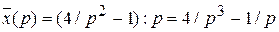Оригинал данного изображения x(t)=2t²-1,и это и есть решение данного уравнения.

Пример 2. Решить задачу Коши.

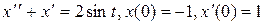
Решение.

Пусть 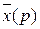- изображение искомого решения x(t), тогд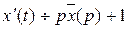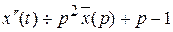а , , а .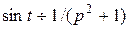

Таким образом, изображение исходного уравнения имеет вид 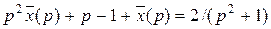, отсюда .

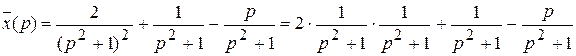Используя таблицу основных изображений и таблицу сверток, получаем, что
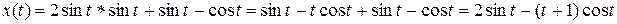Пример 4. Решить задачу Коши.

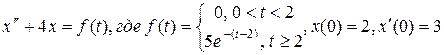
Решение.

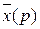Пусть – изображение решения x(t) данного уравнения, тогда , .

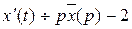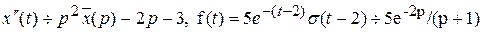Таким образом, изображение исходного уравнения имеет вид : 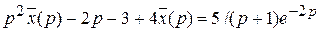, следовательно 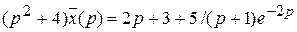, отсюда ;

;

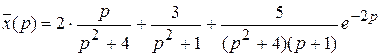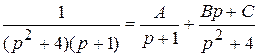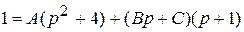
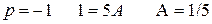
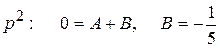
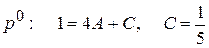
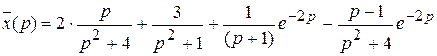, т.о. по таблице изображений и теореме запаздывания получаем, что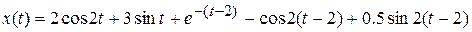

Вопросы для самопроверки

1. Сформулируйте алгоритм решения дифференциального уравнения

Примеры для самостоятельного решения. Решить задачу Коши.

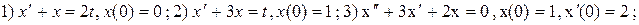
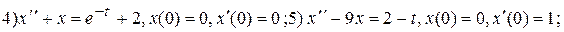
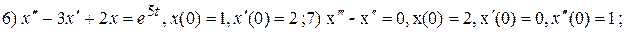
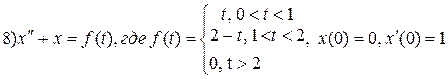
Ответы

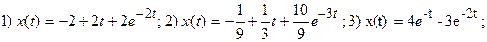
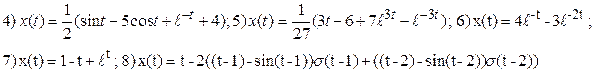
Применение операционного исчисления к решению систем линейных дифференциaльных уравнений.

Системы линейных дифференциальных уравнений решаются аналогично тому, как решаются дифференциальные уравнения.

Рассмотрим несколько примеров.

Пример 1. Найти решение системы.

.

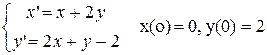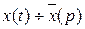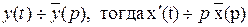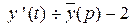Пусть , а , , изображение системы имеет вид :

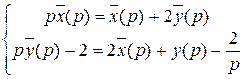или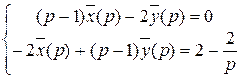

Найдём решение этой линейной системы по формулам Крамера :

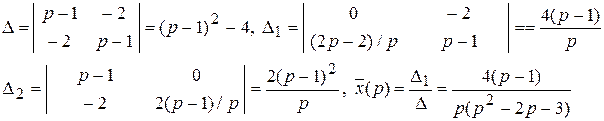
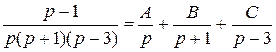
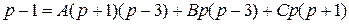
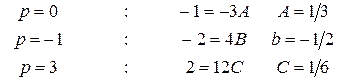
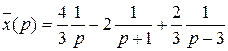, отсюда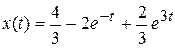

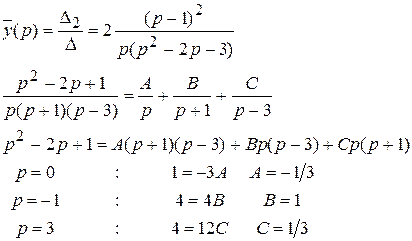
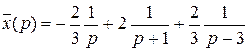, отсюда