Линейная зависимость векторов

Вектор В n-мерного векторного пространства называется пропорциональным вектору А, если существует число k, при котором выполняется соотношение В=kA.

В частности, нулевой вектор пропорционален любому вектору А, так как 0 = 0 • А. Обобщением понятия пропорциональности векторов является понятие линейной комбинации векторов.

Вектор В называется линейной комбинацией векторов A₁, A₂, ..., А_n, если сущест­вуют такие числа k₁, k₂, ..., k_n, при которых выполняется соотношение

B=k₁A₁+ k₂A₂+…+ k_nA_n ,

т. е. j-я компонента вектора В при j = 1, 2, ..., n равна, в соответствии с определениями суммы векторов и произведения вектора на число, сумме произведений j-х компонент векторов A₁, A₂, ..., А_n соответствен­но на числа k₁, k₂, ..., k_n.

Определение 1. Система векторов A₁, A₂, ..., А_r (r³2) называется линейно зависимой, если хотя бы один из векторов системы является линейной комбинацией остальных, и линейно независимой — в противном случае.

Пример. Система векторов В = (8; 5; 11), A₁ = (1; 2; 3), A₂ = (3; 2; 1), Аз = (3; 1; 2) линейно зависима, так как вектор В - линей­ная комбинация векторов А₁, A₂ и Аз, поскольку для него выполняется соотношение В = 2А₁ - А₂ + ЗА₃.

Определение 2. Система векторов A₁, A₂, ..., А_r (r³2) является линейно зависимой, если существуют такие числа k₁, k₂, ..., k_r не все равные ну­лю, при которых имеет место равенство

k₁A₁+ k₂A₂+…+ k_rA_r=0.

Если это соотношение возможно лишь в случае, когда все k_j =0 (j = 1, 2, ..., r), то система векторов называется линейно не­зависимой.

Пример. Система векторов A₁ = (2; 4; 3), А₂ = (2; 3; 1), Аз = (5; 3; 2),А₄ = (1; 7; 3) линейно зависима, так как векторы свя­заны соотношением A₁ + 2A₂ - Аз - А₄ = 0, в котором все коэффи­циенты отличны от нуля.

Теорема. Если некоторая подсистемаA₁, A₂, ..., А_s ( s<r )системы векторовA₁, A₂,...,А_r (r³2) линейно зависима, то и вся системалинейно зависима.

Доказательство.

Пусть подсистема A₁, A₂, ..., А_s линейно зависима; тогда для нее выполняется равенство k₁A₁+ k₂A₂+…+ k_sA_s=0, где не все коэффициенты равны нулю. Присоединяя к этому равенству остальные r - s векторов с нулевыми коэффициентами, получаем

k₁A₁+ k₂A₂+…+ k_sA_s+ 0 ^.A_s+1+…+0 ^.A_r=0

т. е. система A₁, A₂,...,А_r (r³2) линейно зависима.¨

Из теоремы следует, что вообще всякая система векторов, содер­жащая два равных, два пропорциональных вектора или нулевой вектор, является линейно зависимой. Это свойство можно сформулировать по-другому: если система векторов A₁, A₂,...,А_r (r³2) линейно независима, то и всякая ее подсистема также линейно независима.

Теорема.Пусть дана линейно независимая система векторов A₁, A₂,...,А_n . Преобразуем эту систему, прибавляя к одному из ее векторов некоторое кратное другого вектора этой же системы. Тогда новая система векторов также линейно независима.

(без доказательства).

Например. Умножим один из векторов системы, например А₁ на k¹0 и прибавим полученное произведение к А_n, получим новый вектор А_n’=A_n+kA₁, тогда система векторов

A₁, A₂,...,А_n-1,A_n – линейно независимая.

Система векторов остается линейно независимой и в том случае, когда преобразования рассмотренного вида выполняются несколько раз.

Рассматривая линейно зависимую систему векторов, возьмем такую линейно независимую подсистему векторов A₁, A₂,...,А_r (r³2), к которой нельзя присоединить ни одного век­тора системы, не нарушив линейной независимости. Такая подсистема называется максимальной линейно независимой подсистемой данной системы векторов. Число векторов, входящих в любую максимальную линейно независимую подсистему векторов, называется рангом си­стемы.

Пустьдана система векторов

(*)

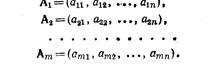Необходимо определить, является она линейно зависимой или нет; если система линейно зависима, то найти, какое числовекторов состав­ляет максимальную линейно независимую подсистему.

Составим из компонент векторов системы матрицу

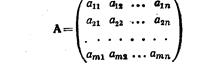
так, чтобы строки матрицы соответствовали векторам A₁, A₂,...,А_m. Тогда поставленную задачу можно решить с помощьюследующей тео­ремы.

Теорема . Максимальное число линейно независимых векторов системы (*) равно рангу матрицы А, составленной из компонент векторов этой системы.

( без доказательства).

Из теоремы следует, что максималь­ное число линейно независимых строк матрицы равно максимальному числу линейно независимых столбцов матрицы и равно рангу этой матрицы. Теорема указывает на один из возможных способов опре­деления линейной зависимости векторов и отыскания максимальной линейно независимой подсистемы данной системы векторов.

Теорема. Любая совокупность n + 1 векторов n-мерного век­торного пространства линейно зависима.

(Без доказательства)