Раздел II КРАТНЫЕ ИНТЕГРАЛЫ

Тема 3 Двойные интегралы

Двойные интегралы. Это задачи на вычисление площадей криволинейных трапеций, вычисление массы тела с переменной плотностью, вычисление интегралов вдоль какой-либо кривой на плоскости или в пространстве и др.

Задача 1. Изобразить на рисунке и найти площадь фигуры, ограниченной данными линиями , .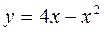

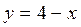Решение.

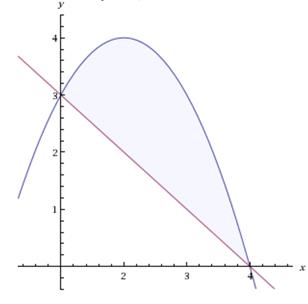
Изобразим фигуру, площадь которой необходимо вычислить. Парабола 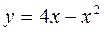изображена синим цветом. Прямая 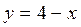изображена красным цветом. (Обратите внимание, что ось сдвинута на 1 вправо).

Находим точки пересечения границ, решая систему:

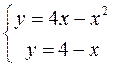
Получаем точк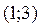и и . Соответственно интеграл для вычисления площади примет вид:

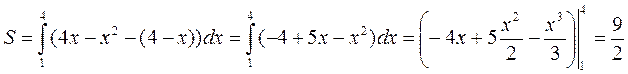Ответ: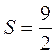

Задача 2. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах: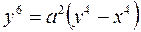

Решение.

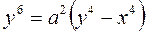
Введём полярные координаты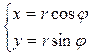

Посмотрим пределы изменения параметра .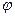

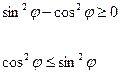
Воспользуемся симметрией фигуры. Найдем площадь части фигуры, лежащей в верхней полуплоскости, и удвоим её.

Ответ.

Задача 3. Пластинка 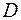задана ограничивающими ее кривыми: x=0, y=0, x+y=2, если поверхностная плотность в каждой ее точке (x,y) задана уравнением 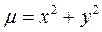. Сделать чертеж. Найти массу пластинки.

Решение.

Для вычисления массы m плоской пластины поданной поверхностной плотностью воспользуемся физическим содержанием двойного интеграла и формулой: m

Аналогично предыдущей задаче строим область интегрирования D.

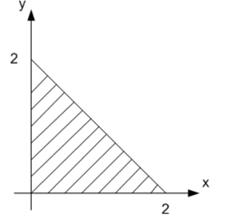
Соответственно интеграл для вычисления массы пластины примет вид:

Ответ: m=8/3 (ед).

Тема 4 Тройные интегралы

Тройные интегралы. Это задачи на вычисление объема прямого цилиндра с плоским основанием, ограниченного сверху некоторой поверхностью, вычисление массы тела с переменной плотностью, вычисление интегралов вдоль какой-либо кривой на плоскости или в пространстве и др.

Задача 4. Найти объем тела, заданного ограничивающими его поверхностями

Решение.

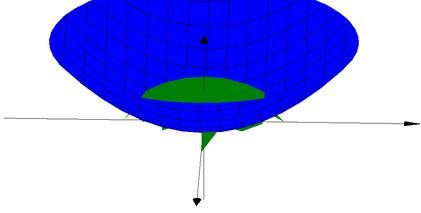
Изобразим тело 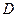, объём которого необходимо вычислить. Тело ограничено 2 эллиптическими параболоидами вдоль z. Поверхность 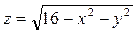изображена зеленым цветом. Поверхность изображена синим цветом.

Тройной интеграл для вычисления объема будет иметь следующий вид.

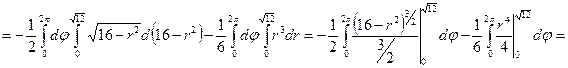
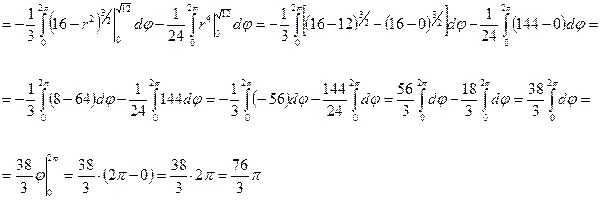
Ответ.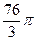

Задача 5. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy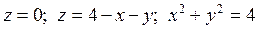

Решение.

Изобразим тело, объем которого необходимо вычислить. Плоскость изображена зеленым цветом. Плоскость 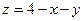изображена красным цветом. Цилиндр 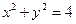изображен синим цветом.

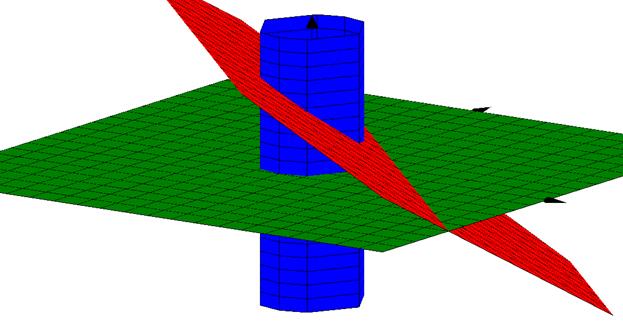
Тройной интеграл для вычисления объема будет иметь следующий вид.

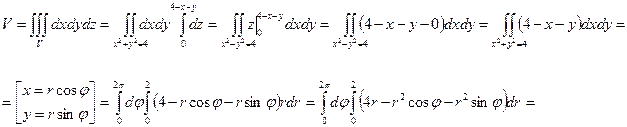
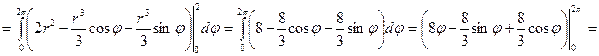
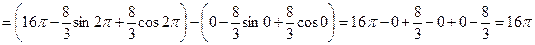
Ответ.

Задача 6. Вычислить с помощью тройного интеграла объем тела, ограни-ченного указанными поверхностями: 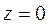, , 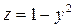, 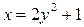. Сделать чертежи данного тела и его проекции на плоскость.

Решение.

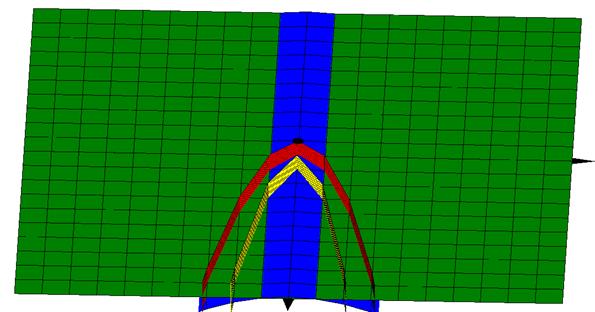
Изобразим тело 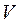, объем которого необходимо вычислить.

Поверхность 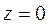изображена зеленым цветом, поверхность 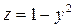– синим цветом, поверхность – красным цветом, поверхность 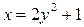– желтым цветом.

Проекция на плоскость 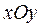имеет вид:

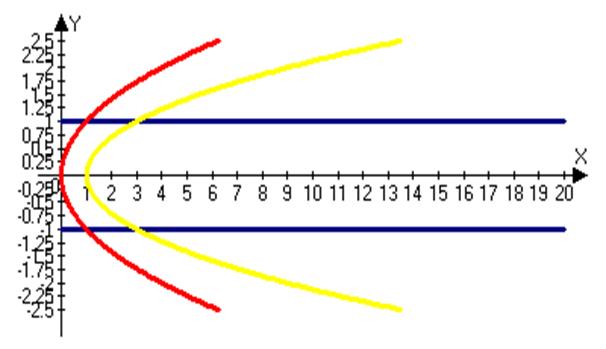
Тройной интеграл для вычисления объема будет иметь следующий вид.

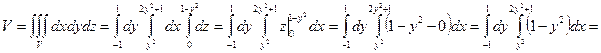
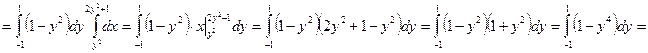
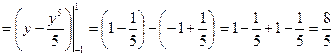
Ответ.

Указания студентам!

1) Во всех задачах обязательно делать рисунки.

2) Рисунки должны быть сделаны простым карандашом (в случае необходимости можно использовать цветные).

3) Варианты выбираются в соответствии со следующей таблицей.

Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий