Основные теоретические сведения. Практикум по эконометрике в среде EXCEL
Практикум по эконометрике в среде EXCEL
Учебное пособие
ОГЛАВЛЕНИЕ
Предисловие ……………………………………………………………………… 5
Глава I. Парная линейная регрессия…………………………………………. 6
1.1. Основные теоретические сведения ..................................................... 6
1.2. Реализация задания на компьютере с помощью ППП Excel ……... 9
1.3. Контрольные задания ………………………………………..………. 17
Вопросы для подготовки к защите индивидуального задания ……….... 31
Глава II. Множественная линейная регрессия……………………………… 32
2.1. Основные теоретические сведения ………………………………... 32
2.2. Реализация задания на компьютере с помощью ППП Excel ……… 36
2.3. Контрольные задания ……………………………………………….. 41
Вопросы для подготовки к защите индивидуального задания ………… 58
Глава III. Нелинейная регрессия……………………………………………….. 60
3.1. Основные теоретические сведения ………………………………… 60
3.2. Реализация задания на компьютере с помощью ППП Excel ……… 62
Вопросы для подготовки к защите индивидуального задания ………… 68
Глава IV. Нарушение предпосылок МНК и их корректировка…………… 69
4.1. Основные теоретические сведения ………………………………... 69
4.1.1. Гетероскедастичность ……………………………………….... 69
4.1.2. Автокорреляция ……………………………………………….. 73
4.1.3. Мультиколлинеарность ………………………………………. 74
4.2. Реализация задания на компьютере с помощью ППП Excel …….... 76
4.2.1. Проверка наличия гетероскедастичности …………………… 77
4.2.2. Проверка наличия мультиколлинеарности …………………. 80
4.2.3. Проверка наличия автокорреляции …………………………. 82
Вопросы для подготовки к защите индивидуального задания ………... 83
Глава V. Временные ряды……………………..……………………………….. 84
5.1. Основные теоретические сведения ………………………………... 84
5.1.1. Основные понятия и определения …………………………… 84
5.1.2. Этапы построения прогноза по временным рядам …………. 85
5.2. Реализация задания на компьютере с помощью ППП Excel ……… 91
5.3. Контрольные задания ………………………………………………... 104
Вопросы для подготовки к защите индивидуального задания ………… 120
Литература ………………………………………………………………………... 121
Приложения ………………………………………………………………………. 122
ПРЕДИСЛОВИЕ
Данное учебное пособие посвящено основам эконометрического моделирования и предназначено для развития у студентов практических навыков решения конкретных экономических и финансовых задач с использованием компьютерных технологий. Под эконометрическим моделированием понимается процесс построения, изучения и применения эконометрических моделей.
Учебное пособие состоит из пяти глав, в которых рассматриваются вопросы линейного регрессионного моделирования (парная и множественная регрессия), нелинейные регрессионные модели и модели временных рядов. При построении модели студенты должны также научиться давать статистическую оценку значимости искажающих эффектов: гетероскедастичности, мультиколлинеарности, автокорреляции и по возможности осуществлять их коррекцию. Этим вопросам посвящена глава 4 «Нарушение предпосылок МНК и их корректировка». Все главы пособия имеют идентичную структуру:
- краткие теоретические сведения, включающие основные понятия, определения, формулы;
- примеры реализации типовых задач на компьютере с помощью ППП Ехсеl;
- задания, включающие набор задач в нескольких вариантах, предлагаемые студентам для самостоятельного решения на компьютере;
- контрольные вопросы, охватывающие основные положения теоретического материала, для подготовки студентов к защите своих индивидуальных заданий.
Примеры решения задач включают фрагмент или полный текст рабочего документа Ехсеl, снабженный комментариями и краткими указаниями, помогающими реализовать решение задачи на компьютере. Решения, полученные в Ехсеl, обведены рамками и представлены в виде рисунков.
Для повышения эффективности изучения дисциплины «Эконометрика» рекомендуется использовать данное пособие для выполнения студентами индивидуальных заданий. Варианты заданий представлены в каждой главе. Итогом курса является их защита.
Глава I
ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Основные теоретические сведения
В общем случае регрессия – функциональная зависимость между объясняющими переменными Хj и объясняемой переменной Y, которая строится с целью прогнозирования среднего значения Y при заданных значениях Хj =xj, 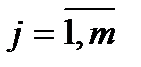 или для анализа влияния отдельных переменных Хj,
или для анализа влияния отдельных переменных Хj, 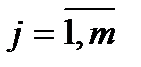 на зависимую переменную.
на зависимую переменную.
Различают уравнения регрессии I и II рода.
Уравнением регрессии первого рода называют уравнение вида:
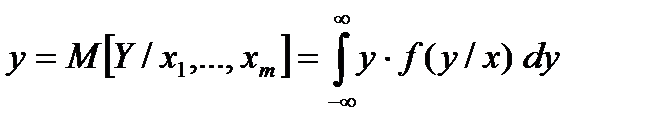 . (1.1)
. (1.1)
Если уравнение (1.1) представляет собой уравнение связи двух случайных величин Y и Х, то это уравнение представляет собой уравнение парной регрессии. В предположении нормального распределения случайной величины (Y, Х) парную регрессию называют линейной парной регрессией, т.к. в этом случае условное математическое ожидание (1.1) представляет собой уравнение прямой линии
Y = M (Y/x) = 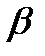 0 +
0 + 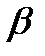 1 Х . (1.2)
1 Х . (1.2)
Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х. В связи с тем, что реальные значения переменной Y не всегда совпадают с ее средним значением M (Y/x), то в уравнение регрессии вводится случайная составляющая 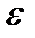 . Тогда уравнение (1.2) можно записать в виде:
. Тогда уравнение (1.2) можно записать в виде:
Y* = M (Y/x) + 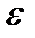 (1.3)
(1.3)
или для конкретных наблюдений (уi , xi ) :
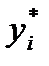 =
= 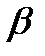 0 +
0 + 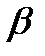 1 xi +
1 xi + 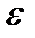 i ,
i , 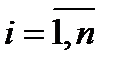 . (1.4)
. (1.4)
Уравнение (1.4) называют теоретической линейной моделью.
Возмущения 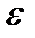 i ,
i , 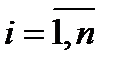 должны удовлетворять основным предпосылкам регрессионного анализа:
должны удовлетворять основным предпосылкам регрессионного анализа:
1. Математическое ожидание возмущения 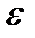 i равно нулю
i равно нулю
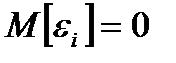
или
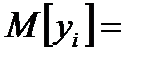
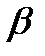 0 +
0 + 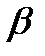 1 xi .
1 xi .
2. Дисперсия возмущения 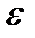 i постоянна для любого i, т.е.
i постоянна для любого i, т.е.
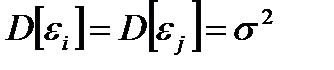 ,
, 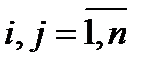 .
.
3. Возмущения 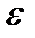 i и
i и 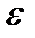 j являются независимыми друг от друга, что влечет за собой отсутствие автокорреляции
j являются независимыми друг от друга, что влечет за собой отсутствие автокорреляции
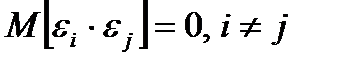 .
.
4. Возмущения 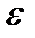 i представляет собой нормально распределенную случайную величину.
i представляет собой нормально распределенную случайную величину.
Обычно исследователь имеет дело с исходными данными выборки объемом n, где каждое наблюдение – есть точка (Y, Х) в (m+1) – мерном пространстве. Здесь m – число объясняющих переменных.
В случае парной регрессии имеется выборка объемом n двумерной случайной величины (Y, Х).
Уравнением регрессии второго рода называют эмпирическое уравнение регрессии, которое строится на основе данных выборки.
Рассматривается парная линейная регрессия, когда уравнение регрессии второго рода имеет вид
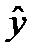 i = М[Y/X=x] = b0 + b1 xi ,
i = М[Y/X=x] = b0 + b1 xi , 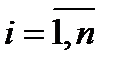 . (1.5)
. (1.5)
С учетом уравнения (1.3) эмпирическую линейную модель связи переменных Y и Х запишем в виде:
yi = b 0 + b 1 xi + ei , (1.6)
где 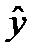 i , b0 , b1 , e i – оценки соответственно yi,
i , b0 , b1 , e i – оценки соответственно yi, 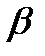 0,
0, 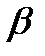 1,
1, 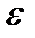 i .
i .
Построение уравнения регрессии начинается с построения корреляционного поля, представляющего собой графическую зависимость в виде точек случайной величины (Y, Х) на плоскости y0x. По расположению эмпирических точек делается вывод о наличии линейной корреляционной зависимости между переменными Y и Х. Дальнейшее построение уравнения регрессии сводится к оценке ее параметров, используя метод наименьших квадратов (МНК). В этом случае неизвестные параметры b0 и b1 выбираются так, чтобы сумма квадратов отклонений эмпирических значений yi от значений 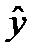 i , найденных по уравнению регрессии (1.5), была минимальной
i , найденных по уравнению регрессии (1.5), была минимальной
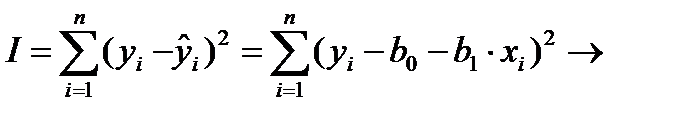 min.
min.
Применение МНК обусловлено тем, что он позволяет получить несмещенные оценки с минимальной дисперсией, в условиях, когда 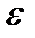 i удовлетворяют всем предпосылкам регрессионного анализа.
i удовлетворяют всем предпосылкам регрессионного анализа.
В результате операции МНК оценка выборочного коэффициента регрессии b1 определяется выражением:
b1 = Cov (X,Y) / 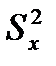 , (1.7)
, (1.7)
а коэффициента b0 :
b0 = 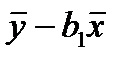 , (1.8)
, (1.8)
где 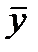 =
= 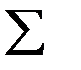 уi /n;
уi /n; 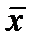 =
= 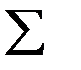 хi /n; Cov (X,Y) =
хi /n; Cov (X,Y) = 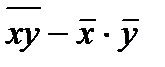 ;
; 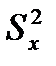 =
= 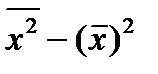 .
.
Точность оценок коэффициентов линейного уравнения регрессии первого рода характеризуется их выборочными дисперсиями, которые вычисляются по формулам:
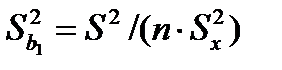 , (1.9)
, (1.9)
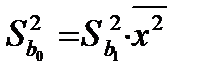 . (1.10)
. (1.10)
Здесь S2 – дисперсия регрессии – оценка дисперсии 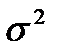 , определяемая по формулам: S2 =
, определяемая по формулам: S2 = 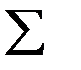 еi2 /(n – 2), еi = yi - b0 - b1 xi .
еi2 /(n – 2), еi = yi - b0 - b1 xi .
Проверка качества уравнения регрессии осуществляется по ряду позиций.
Оценка статистической значимости коэффициентов регрессии заключается в проверке основной гипотезы Н0 о значимости отличия коэффициентов b0 и b1 от нуля. С этой целью используется критерий Стьюдента. Вычисляются , и сравниваются с tкрит . Результатом сравнения является вывод о значимости коэффициентов b0 и b1 .
2. Интервальные оценки коэффициентов уравнения регрессии.
Так как объем выборки ограничен, то b0 и b1 – случайные величины, поэтому желательно найти доверительные интервалы для истинных значений 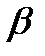 0 ,
0 , 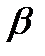 1. Для этого также используется статистика
1. Для этого также используется статистика
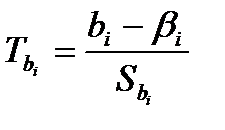 , i = 0,1,
, i = 0,1,
которая имеет t – распределение Стьюдента с 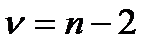 степенями свободы. Интервальные оценки параметров
степенями свободы. Интервальные оценки параметров 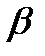 i при заданном уровне значимости
i при заданном уровне значимости 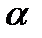 имеют вид
имеют вид
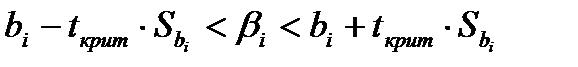 , i = 0,1,
, i = 0,1,
с надежностью р = 1- 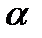 . Здесь tкрит – критическое значение распределения Стьюдента, взятое из таблицы с параметрами
. Здесь tкрит – критическое значение распределения Стьюдента, взятое из таблицы с параметрами 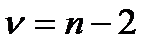 и
и 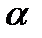 /2.
/2.
3. Проверка значимости уравнения регрессии в целом.
Позволяет установить, соответствует ли математическая модель экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Мерой общего качества уравнения регрессии является коэффициент детерминации R2 :
R2 = 1 - 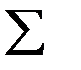 еi2 /
еi2 / 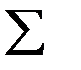 ( yi -
( yi - 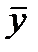 )2 . (1.11)
)2 . (1.11)
Выражение (1.11) вытекает из соотношения:
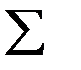 ( yi -
( yi - 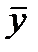 )2 =
)2 = 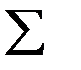 ki2 +
ki2 + 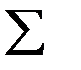 ei2 , (1.12)
ei2 , (1.12)
где 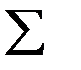 ki2 =
ki2 = 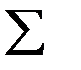 (
( 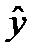 i -
i - 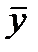 )2 – объясненная регрессией сумма квадратов. Характеризует разброс, обусловленный регрессией;
)2 – объясненная регрессией сумма квадратов. Характеризует разброс, обусловленный регрессией;
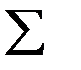 ei2 =
ei2 = 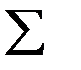 ( yi -
( yi - 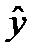 i)2 – остаточная (необъясненная) сумма квадратов – характеризует случайную составляющую разброса yi относительно линии регрессии
i)2 – остаточная (необъясненная) сумма квадратов – характеризует случайную составляющую разброса yi относительно линии регрессии 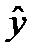 .
.
Из соотношений (1.11) и (1.12) следует, что коэффициент детерминации R2 есть не что иное, как:
R2 = 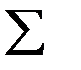 ki2 /
ki2 / 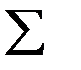 ( yi -
( yi - 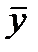 )2. (1.13)
)2. (1.13)
Таким образом, коэффициент детерминации можно вычислить по (1.11) или по (1.13).
Основная цель использования уравнения регрессии - прогноз значений зависимой переменной.
Здесь речь идет о возможных значениях Yр при определенных значениях объясняющей переменной Хр. Так как задача решается в условиях неопределенности то прогноз удобнее всего давать на основе интервальных оценок, построенных с заданной надежностью 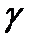 .
.
Причем здесь возможно два подхода: 1) предсказание среднего значения, т.е. M (Y/ Х=xр); 2) предсказание индивидуальных значений Y/ Х=xр .
Интервальный прогноз для среднего значения вычисляется следующим образом:
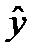 р
р  tкр S
tкр S 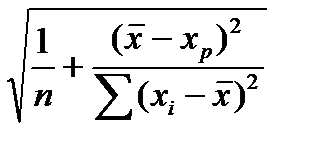 , (1.14)
, (1.14)
где 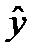 р = b0 + b1xр ; tкр – критическое значение, полученное по распределению Стьюдента при количестве степеней свободы
р = b0 + b1xр ; tкр – критическое значение, полученное по распределению Стьюдента при количестве степеней свободы  = n – 2 и заданной вероятности
= n – 2 и заданной вероятности  /2.
/2.
Интервальный прогноз для индивидуального значения вычисляется по формуле:
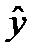 р
р  tкр S
tкр S 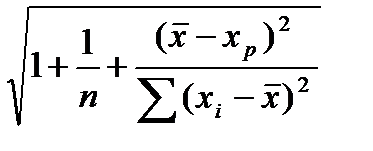 . (1.15)
. (1.15)
