Дұрыстығын дәлелдеуде қолдану
Лекция
Математиканы оқытудағы индукяция және дкдукци.Математикалық индукция әдісі.
Жоспары:
1. Индукция.
1.1. Толымсыз индукция;
1.2. Толық индукция;
1.3. Математикалық индукция.
2. Математикалық индукция әдісінің теоремаларды дәлелдеуде
қолданылуы
3. Математикалық индукция әдісінің сандардың бөлінгіштігін дәлелдеуде қолдануы
4. Математикалық индукция әдісін теңбе-тендіктердің дұрыстығын дәлелдеуде қолдану
5. Математикалық индукция әдісін теңсіздіктің
дұрыстығын дәлелдеуде қолдану
7. Дедукция
ндукция және дедукция өзара байланысты таным әдістері. Бұл әдістердің бөлінуі ой қорытулардың индуктивтік және дедуктивтік болып ажыратылуына негізделген. Индукция (лат. Inducti-бағыттау), дедукция (лат. Deductіо-қорытындылау, шығару) терминдерінің үш мәні бар:
1) ой қорытулардың түрлері;
2) зерттеу әдістері;
3) материалды баяндау формалары.
1. Индукция.
Индукция деп әдетте жекеден жалпыға өтудегі ой қорыту түсініледі. Индукция туралы кең мағынада, ойлау қозғалысының жеке жағдайлардан жалпы жағдайға көшу нәтижесіндегі таным әдісі; тану амалы деп айтуға болады. Жалпы алғанда, математикада индуктивті әдіс деп тәжірибе арқылы тексерілген және дұрыстығы қатаң түрде тағайындалған теориялық сипаттағы айғақтар негізінде жаңа қорытындылар және теориялар алу деп түсініледі.
Математикада теоремаларды дәлелдеуде, есептерді шығаруда көп қолданылатын әдістердің бірі индукция мен дедукция деп аталады. Бұл әдістердің негізіне түсіну үшін алдымен ойды қорытындылаудың қандай түрлері болатынын қарастырайық. Ойды тұжырымдаудың екі түрі болады. Мысалы, “120” саны 5-ке бөлінеді десек, тек бір ғана санның (120-ның), екінші бір санға (5-ке) бөлінетінін айттық. Сондықтан бұл жеке фактыны қарастыру арқылы жасалынған дербес тұжырым. Бөлінгіш (120) нольмен аяқталған үш таңбалы сан оның осы екі қасиетін байқап алып, мынадай жалпы екі ой қорытындысын жасайық:
1. Нольмен аяқталған сандардың барлығы 5-ке бөлінеді.
2. Үш таңбалы сандардың барлығы 5-ке бөлінеді.
Бұл екі пікірдің біріншісі дұрыс болғанымен, екіншісі бұрыс, өйткені үш таңбалы сандардың барлығы бірдей 5-ке бөліне бермейді.
Осындай жеке ой қорытындысынан жасалынған жалпы ой қорытындысын индукция (лат.inductio-ой салу) деп атайды.
Сөйтіп, дербес фактыларды қарастырып, яғни индукция жолымен жасалынған жалпы ой қорытындысы дұрыс та, теріс те болуы мүмкін. Енді ол қай уақытта дұрыс және қай уақытта теріс болатындығына көз жеткізу үшін индукцияның қандай түрлері болатынын қарастырайық. Индукция 3 түрлі болады:
1. Толымсыз индукция;
2. Толық индукция;
3. Математикалық индукция.
1.1. Толымсыз индукция. Жеке фактылар өте көп болып, бірақ олардың барлығын қарастырмай, тек кейбіреулерін ғана қарастырып, олардағы ерекшеліктерді байқап алып, сол арқылы жалпы қорытынды жасайтын болсақ, ол толымсыз индукция болады.
Сонымен, толымсыз индукдия дегеніміз зерттеліп отырған құбылыстың, объектілердің барлық жағдайларын қамтымайтын алғы шарттардан шығатын жалпы ой қорытындысы.
Толымсыз индукция жасаған қорытынды дұрыс болмауы мүмкін, өйткені алғашқы жеке фактыларда бар ерекшелік кейінгілерінде болмайтын жағдай болады. Сондықтан толымсыз индукция барлық жеке жағдайлар түгел қарастырылмағандықтан, бұған сүйеніп айтылған қорытынды дұрыс бола бермейді. Сондықтан бұл ғылыми дәлелдеудің қатаң түрі бола алмайды.
Мысалы, математика тарихынан толымсыз индукцияны қолданып теріс қорытындылар жасалынған жағдайларды көптеп кездестіреміз. Мысалы, француз математигі Ферма (1601-1665) 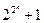 формуладағы n-нің дербес
формуладағы n-нің дербес 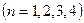 мәндерін қарастырып келіп, бұл саннан әрқашан жай сан шығады деп жорыған. Кейін оны Л.Эйлер (1707-1783) тексере келіп,
мәндерін қарастырып келіп, бұл саннан әрқашан жай сан шығады деп жорыған. Кейін оны Л.Эйлер (1707-1783) тексере келіп, 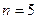 болғанда жай сан болмайтынын тапқан.
болғанда жай сан болмайтынын тапқан.
Ерекшелігін Л.Эйлер көрсеткен үш мүшедегі 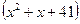 х-ке қандай мән берілсе де, одан жай сан береді деп білген, бір кезде. Кейін х-тің дербес мәндерін тексере келіп,
х-ке қандай мән берілсе де, одан жай сан береді деп білген, бір кезде. Кейін х-тің дербес мәндерін тексере келіп, 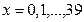 болғанда жай сан, ал
болғанда жай сан, ал 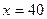 болғанда құрама сан шығатыны байқалған.
болғанда құрама сан шығатыны байқалған.
Бірақ солай бола тұрса да толымсыз индукцияның ғылымда маңызы күшті. Оның пайдасы белгілі бір зерттеу мәселесінде кейбір жеке жағдайларды қарастыру арқылы сәйкес заңдылықты байқап, жалпы қорытындының қандай болатынын жобалауға болады. Мысалы, Атақты Гольбдах проблемасы, Ферманың ұлы теоремасы толымсыз индукция арқылы тұжырымдалған.
Арифметикада сандардың бөлінгіштік белгілері көбінесе толымсыз индукция әдісімен түсіндіріледі.
1.2. Толық индукция. Толық индукция дегеніміз – зерттеліп отырған құбылыстың немесе объектінің барлық жағдайларын толық қамтитын алғы шарттардан жалпы қорытынды шығаруға болатын индукциялық ой қорытындысы.
Мысалы, бір кластағы 30 оқушының әрқайсысының да сабақтан үлгеретіндігі тексеріліп анықталса, онда бұл жеке алғы шарттардан: “бұл кластың барлық оқушылары сабақтан үлгереді” деген дұрыс пікір айтуға болады.
Математикадан мынадай мысал келтірейік. Геометрияда: “Іштей сызылған бұрыш өзінің тірелетін доғасының жартысымен өлшенеді” деген теорема бар.
Бұл теореманы дәлелдеуде үш түрлі жеке жағдайды қарастырамыз:
1. шеңбердің центрі бұрыштың ішінде жатады;
2. шеңбердің центрі бұрыштың сыртында жатады;
3. шеңбердің центрі бұрыштың қабырғасында жатады.
Бұл келтірілген үш түрлі жағдайдан басқа жағдай кездесуі мүмкін емес. Сондықтан барлық жеке жағдайлары қамтылды деуге болады. Осылардың әрқайсысы үшін теоремадағы айтылған пікір дұрыс болғандықтан, барлық жағдайда да оны ақиқат десек қателеспейміз.
Қорытып айтқанда, толық индукцияға сүйеніп айтылған ой қорытындысы әр уақытта ақиқат болады.
Бірақ математикада толық индукцияны жиі қолдануға мүмкіндік бермейтін қолайсыз жағдай бар. Оның себебі, белгілі ой қорытындысын шығару үшін жоғарыдағы көрсетілгендей барлық жеке жағдайларды тексеру керек. Ал математикада ондай жеке жағдайлардың шексіз болып келетіні жиі кездеседі. Ондай пікірлердің ақиқаттығына толық индукция арқылы көз жеткізу мүмкін емес.
1.3. Математикалық индукция жасалған қорытынды бірнеше дербес жағдайлар үшін дұрыс болса, дербес жағдайлар өте көп болғандықтан олардың барлығын бірдей қарастыру мүмкін болмаса, бірақ сол қорытындының жалпы дұрыстығын қалайда білу керек болса, онда математикалық индукция әдісі қолданылады.
Математикалық индукция әдісінің негізіне мынадай принцип жатады.
Қандай да пікір 1. Натурал сан 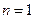 болғанда дұрыс болса және 2. Бұл пікірдің кез келген
болғанда дұрыс болса және 2. Бұл пікірдің кез келген 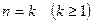 мәні үшін дұрыстығынан, оның
мәні үшін дұрыстығынан, оның 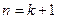 үшін де дұрыс болатындығы тағайындалса, онда бұл пікір кез келген натурал сан
үшін де дұрыс болатындығы тағайындалса, онда бұл пікір кез келген натурал сан 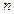 үшін дұрыс болады.
үшін дұрыс болады.
Расында да, 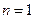 болғанда пікіріміз 1. бойынша дұрыс. Одан кейін,
болғанда пікіріміз 1. бойынша дұрыс. Одан кейін, 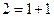 сондықтан
сондықтан 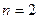 болғанда пікіріміз 2. бойынша дұрыс;
болғанда пікіріміз 2. бойынша дұрыс; 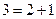 , сондықтан
, сондықтан 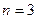 болғанда пікіріміз 3. бойынша дұрыс болады. Жалпы алғанда, кез келген натурал n-саны 1 санына
болғанда пікіріміз 3. бойынша дұрыс болады. Жалпы алғанда, кез келген натурал n-саны 1 санына 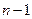 рет біртіндеп бірді қосу нәтижесінде шығады. 1-ді осылайша әр жолы қосқан сайын натурал сан шығады, ол сан үшін қарастырып отырған пікіріміз дұрыс болады. Сондықтан ол пікір натурал сан п саны дұрыс болады.
рет біртіндеп бірді қосу нәтижесінде шығады. 1-ді осылайша әр жолы қосқан сайын натурал сан шығады, ол сан үшін қарастырып отырған пікіріміз дұрыс болады. Сондықтан ол пікір натурал сан п саны дұрыс болады.
Қазіргі мағынасындағы индукция әдісін ең алғаш қолданған француз ғалымы Б.Паскаль (1623-1662) болатын.
Алдымен индукция методының математикада қолданылуына мысалдар келтірейік.
Индукция методы арқылы ой қорытындысын белгілі бір математикалық ереженің үш жағдай үшін дұрыстығы тексеріліп, барып одан кейін оның п үшін дұрыстығына қорытынды шығарылады.
1-мысал. 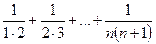 қосындысын есептейік.
қосындысын есептейік.
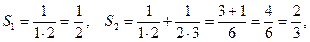
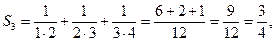
.........................................................
Осы үш қосындыға сүйеніп, жалпы жағдай үшін мынаны жазамыз:
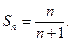
Мектептегі алгебра курсында дәреже мен логарифмнің қасиеттері өтілгеннен кейін, осы қасиеттерге сүйеніп оқушылар индуктивтік ой қорытындысын шығару арқылы дәреже мен логарифмнің жалпыланған қасиеттерін шығарулары мүмкін.
2-мысал.
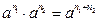
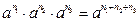
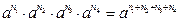
.....................................
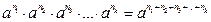
3-мысал. 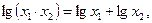 егер
егер 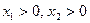
болса,
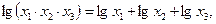 егер
егер 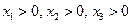
болса,
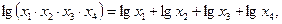 егер
егер 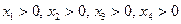 болса,
болса,
..........................................................................................................
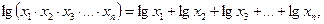 егер
егер 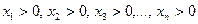 болса.
болса.
2. Математикалық индукция әдісінің теоремаларды дәлелдеуде
қолданылуы
Математикалық индукция әдісін қолданып, мектеп матемаика курсындағы көптеген теоремаларды дәлелдеуге болады.
Мысалы, математикалық индукция әдісін қолданып, “Арифметикалық прогрессияның кез келген мүшесі бірінші мүшеге оның алдындағы мүшелердің санын прогрессияның айырмасына көбейтіп қосқанға тең болатындығын”, яғни арифметикалық прогрессияның кез келген мүшесінің мына формуламен 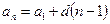 (1) анықталатындығын дәлелдейік.
(1) анықталатындығын дәлелдейік.
Шынында да, біріншіден 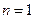 болса,
болса, 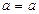 дұрыс теңдік шығады. Енді кез келген п үшін келтірілген (1) формуланы дұрыс деп алып, оның
дұрыс теңдік шығады. Енді кез келген п үшін келтірілген (1) формуланы дұрыс деп алып, оның 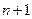 үшін сол заңдылықтың орындалатындығын, яғни
үшін сол заңдылықтың орындалатындығын, яғни 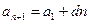 екендігін көрсетейік. Ол үшін (1) тендіктің екі жағына да d-ны қоссақ:
екендігін көрсетейік. Ол үшін (1) тендіктің екі жағына да d-ны қоссақ:
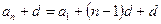 шығады. Мұнан
шығады. Мұнан 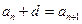 болғандықтан (1) тендіктің дұрыстығы математикалық индукция әдісімен дәлелденді.
болғандықтан (1) тендіктің дұрыстығы математикалық индукция әдісімен дәлелденді.
Сонымен, арифметикалық прогрессияның кез келген мүшесінің 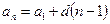 формуласымен анықталатындығы дәлелденді.
формуласымен анықталатындығы дәлелденді.
3. Математикалық индукция әдісінің сандардың бөлінгіштігін дәлелдеуде қолдануы
Математикалық индукция әдісі сандардың бөлінгіштігін дәлелдеуде жиі қолданылады.
Мысалы: 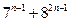 санының n-нің кез келген натурал мәнінде 19-ға бөлінетіндігін дәлелдеңдер.
санының n-нің кез келген натурал мәнінде 19-ға бөлінетіндігін дәлелдеңдер.
Дәлелдемесі: Егер 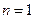 болса, онда
болса, онда 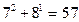 болады да, бұл сан 19-ға бөлінеді. Айталық енді натурал п саны үшін
болады да, бұл сан 19-ға бөлінеді. Айталық енді натурал п саны үшін 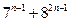 саны 19-ға бөлінсін. Сонда
саны 19-ға бөлінсін. Сонда 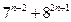 санының да 19-ға бөлінетіндігін көрсетейік.
санының да 19-ға бөлінетіндігін көрсетейік.
Расында да
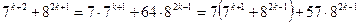 болатындықтан және сандардың (қосылғыштардың) әрқайсысы 19-ға бөлінетіндіктен,
болатындықтан және сандардың (қосылғыштардың) әрқайсысы 19-ға бөлінетіндіктен, 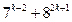 саны 19-ға бөлінеді. Есептің тұжырымы дәлелденді.
саны 19-ға бөлінеді. Есептің тұжырымы дәлелденді.
4. Математикалық индукция әдісін теңбе-тендіктердің дұрыстығын дәлелдеуде қолдану
1-мысал: n-нің кез келген натурал мәндерінде 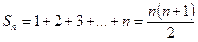 тендігінің орындалатынын дәлелдеңдер.
тендігінің орындалатынын дәлелдеңдер.
Дәлелдеуі. Егер 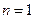 болса, онда
болса, онда 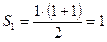 болады. Айталық,
болады. Айталық, 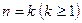 саны үшін бұл теңбе-теңдік дұрыс болсын, яғни
саны үшін бұл теңбе-теңдік дұрыс болсын, яғни 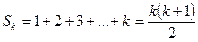 . Сонда
. Сонда 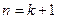 үшін бұл теңбе-теңдіктің дұрыс болатындығын, яғни
үшін бұл теңбе-теңдіктің дұрыс болатындығын, яғни 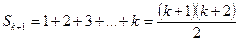 болатынын көрсетейік. Ол үшін алдыңғы теңбе-теңдіктің дұрыстығын пайдаланамыз:
болатынын көрсетейік. Ол үшін алдыңғы теңбе-теңдіктің дұрыстығын пайдаланамыз:
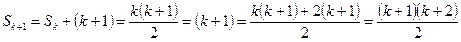
Демек, 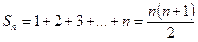 қосындысын есептеу формуласы дұрыс екен.
қосындысын есептеу формуласы дұрыс екен.
Сонымен, есептің тұжырымы дәлелденді.
2-мысал: Теңбе-теңдікті дәлелдеңдер:
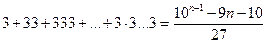
Дәлелдеуі: 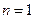 болғанда, теңдік орындалады.
болғанда, теңдік орындалады.
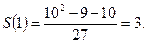
Айталық, енді бұл теңдік 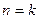 үшін дұрыс болғанда
үшін дұрыс болғанда 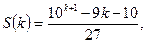 оның
оның 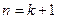 үшін дұрыс болатындығын, яғни
үшін дұрыс болатындығын, яғни 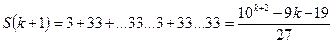 орындалатыңдығын дәлелдейміз.
орындалатыңдығын дәлелдейміз.
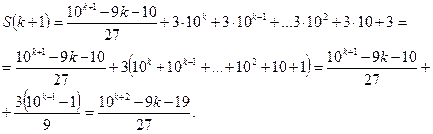
Сонымен, жоғарыдағы теңдіктің кез келген натурал сан п үшін дұрыстығы дәлелденді.
5. Математикалық индукция әдісін теңсіздіктің
дұрыстығын дәлелдеуде қолдану
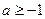 болғанда, кез келген натурал п саны үшін мына теңсіздіктің
болғанда, кез келген натурал п саны үшін мына теңсіздіктің 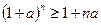 (1) орындалатындығын дәлелдеңдер.
(1) орындалатындығын дәлелдеңдер.
Дәлелдеуі. 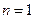 үшін (1)теңсіздік дұрыс, өйткені
үшін (1)теңсіздік дұрыс, өйткені 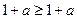 . Енді біз (1) теңсіздіктің
. Енді біз (1) теңсіздіктің 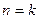 натурал саны үшін дұрыс депжорығанда
натурал саны үшін дұрыс депжорығанда 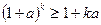 (2)оның
(2)оның 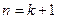 саны үшін дұрыс болатындығын, яғни
саны үшін дұрыс болатындығын, яғни 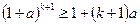 (3)теңсіздігінің орындалатындығын көрсетейік. Ол үшін (2) теңсіздіктің екі жағында
(3)теңсіздігінің орындалатындығын көрсетейік. Ол үшін (2) теңсіздіктің екі жағында 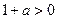 -гекөбейтеміз. Сонда
-гекөбейтеміз. Сонда 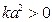 болатындықтан,
болатындықтан, 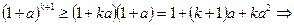
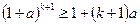 болады.
болады.
Сондықтан математикалық индукция әдісі бойынша (1) теңсіздік кез келген натурал п саны үшін дұрыс болады.
Бұл теңсіздікті Бернулли теңсіздігі деп атайды.
