Классический метод анализа переходных процессов

Законы коммутации и начальные условия.

В общем случае переходный процесс занимает некоторое (теоретически бесконечно большое) время. Например, можно услышать как постепенно снижается до нулевой громкость звука работающего радиоприемника при отключении его от источника электропитания.

Любой установившийся режим характеризуется определенным запасом энергии магнитного и электрического полей в каждый момент времени

, (1.1)

где ik (ul) - мгновенный ток (напряжение) в катушке Lk (на конденсаторе Cl ); k и l - индексы суммирования.

В переходном режиме происходит изменение запасенной в цепи энергии и это изменение не может происходить скачкообразно (мгновенно), так как скачкообразное изменение энергии потребует бесконечно больших мощностей P = dW / dt в цепи, что лишено физического смысла.

На основании этого вывода и соотношения (1.1) могут быть сформулированы два закона коммутации при конечных по величине воздействиях в цепи.

1. Ток в любом индуктивном элементе является непрерывной функцией времени и не может изменяться скачком, в частности для момента коммутации t = 0

iL(0+) = iL(0-) = iL(0) ,(1.2)

где t = 0- - момент времени непосредственно предшествующий моменту коммутации; t = 0+ - момент времени сразу после мгновенной коммутации.

2. Напряжение на любом емкостном элементе является непрерывной фуекцией времени и не может изменяться скачком. В частности для момента коммутации

uC(0+) = uC(0-) = uC(0) ,(1.3)

Таким образом, токи в индуктивностях и напряжения на емкостях в начальный момент t = 0+ после коммутации имеют те же значения, что и непосредственно перед коммутацией при t = 0- и затем плавно изменяются. Заметим, что токи и напряжения на резисторах, а также токи через емкости и напряжения на индуктивностях могут изменяться скачкообразно, так как с ними непосредственно не связана запасаемая в цепи энергия.

Начальные условия

Значения напряжений на емкостях и токов в индуктивностях цепи в момент коммутации, т. е. в начальный момент, образуют независимые начальные условия задачи. Независимые начальные условия определяют начальный запас энергии в цепи. Различают задачи с нулевыми начальными условиями, когда для всех емкостей uC(0+) = 0 и для всех индуктивностей iL(0+) = 0, и с ненулевыми, когда указанные требования нарушаются хотя бы в одном из реактивных элементов. Независимые начальные условия могут быть заданы или рассчитаны с применением законов коммутации.

Начальные значения токов в ветвях без катушек индуктивности или напряжений на элементах, не являющихся конденсаторами, называются зависимыми начальными условиями. Они определяются по независимым начальным условиям с применением законов Кирхгофа или других методов расчета для момента времени t = 0+.

Классический метод анализа переходных процессов

Классический метод анализа переходных процессов основан на составлении системы дифференциальных и алгебраических уравнений с использованием уравнений для элементов и законов Кирхгофа для мгновенных токов и напряжений в цепи:

Для определения интересующей реакции систему исходных уравнений путем исключения остальных переменных приводят к одному линейному уравнению n-го порядка с постоянными коэффициентами:

,(1.4)

где i(t) - искомая переменная; f(t) - правая часть, обусловленная возмущающими силами, т.е. функциями источников.

Напомним известные из курса математики сведения о решении линейных дифференциальных уравнений. Общее решение линейного дифференциального уравнения (1.4) определяется в виде суммы двух составляющих:

i(t) = iсв(t) + iвын(t) . (1.5)

Первая составляющая называется свободной или собственной и определяется как общее решение соответствующего однородного уравнения, которое получается из (1.4) путем приравнивания нулю правой части f(t) = 0:

(1.6)

Для определения общего решения (1.6) составляется характеристическое уравнение, которое получается из (1.6) путем замены k -той производной на pk . При этом сама искомая переменная заменяется на единицу. Характеристическое уравнение

pⁿ + b_n-1p^n-1 + ........... +b₁p + b₀ = 0(1.7)

является алгебраическим уравнением степени n и его корни pk определяют общее решение однородного дифференциального уравнения:

, (1.8)

где Ak - постоянные интегрирования.

Решение (1.8) записано для случая различных корней pk . Входящие в (1.8) n постоянных интегрирования определяются по известным независимым начальным условиям.

Заметим, что в однородном дифференциальном уравнении (1.6) правая часть приравнивается нулю, что означает отсутствие в цепи внешнего воздействия, т.е. источника. Поэтому токи и напряжения в ветвях цепи будут определяться только параметрами и свойствами самой цепи, а также начальным запасом энергии. Физически очевидно, что для реальных цепей собственная составляющая i_св(t) при отсутствии источников должна стремиться со временем к нулю. Эта составляющая существует во время переходного процесса.

Вторая составляющая i_вын(t) решения (1.5) называется вынужденной и представляет собой частное решение неоднородного дифференциального уравнения (1.4) (с ненулевой правой частью). Из математики известно, что вид частного решения определяется видом правой части уравнения. В частности, если правая часть f(t) - константа, то и частное решение ищется в виде константы. Если правая часть является гармонической функцией с определенными частотой, амплитудой и начальной фазой, то и частное решение будет гармонической функцией той же частоты, для которой нужно определить амплитуду и начальную фазу.

Таким образом, вынужденная составляющая обусловлена воздействием источников в цепи и при t ®Ґ искомая переменная i(t) ® i_вын(t). Поэтому вынужденная составляющая называется установившейся и определяется как установившееся значение (в случае постоянной вынуждающей силы) или как установившаяся функция (в случае гармонической вынуждающей силы) для искомой переменной в цепи после коммутации

i_вын(t) = i_уст(t) (1.9)

Необходимо отметить, что определение вынужденной составляющей в случае воздействия сигналов более сложной формы, чем упомянутые выше, представляет достаточно сложную задачу.

В заключении приведем рекомендуемый порядок расчета переходных процессов классическим методом.

1. Определить независимые начальные условия iLk(0+) и uCk(0+) с использованием законов коммутации.

2. Для цепи после коммутации составить систему уравнений Кирхгофа с использованием уравнений для элементов.

3. Полученную систему разрешить относительно искомой переменной. При этом получится одно дифференциальное уравнение n-ой степени, где n равно общему числу индуктивностей и емкостей, в которых можно задавать независимые начальные условия.

4. Определить решение полученного дифференциального уравнения

(1.10)

где iвын(t)=iуст(t) -вынужденная (установившаяся) составляющая; pk - корни характеристического уравнения; Ak - постоянные интегрирования, определяемые из начальных условий.

3. Переходный процесс в r, L – цепи при включении на источник постоянного напряжения

1. i_L(0-)=0

2. i_уст=E/r

3. a)ri+Ldi/dt=E b)z(jw)=r+jwL

Lp+r=0 jw 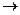p

p=-r/L z(p)=0

0=pL+r p=-r/L

i_Lсв(t)=Ae^pt

4. i_L(t)=i_уст+i_св(t)=E/r+Ae^pt

i_L(0)=E/r+A 0=E/r+A

5. i_L(t)=E/r(1-e^-rt/r)