Функцияның ақырсыздықтағы шегі
Анықтама. Кезкелген 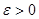 (
( 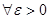 ) саны үшін қандай да бір
) саны үшін қандай да бір 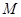 саны табылып,
саны табылып, 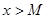 болғанда
болғанда 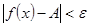 орындалса, онда
орындалса, онда 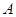 саны
саны  функциясының
функциясының 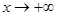 шегі деп аталады және
шегі деп аталады және 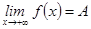 түрінде белгіленеді.
түрінде белгіленеді.
Анықтама. 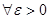 саны үшін,
саны үшін, 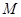 саны табылып,
саны табылып, 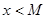 болғанда
болғанда 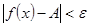 орындалса, онда
орындалса, онда 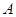 саны
саны  функциясының
функциясының 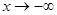 шегі деп аталады және
шегі деп аталады және 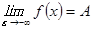 түрінде белгіленеді.
түрінде белгіленеді.
Анықтама. 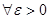 үшін,
үшін, 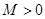 саны табылып,
саны табылып, 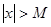 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын 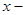 тер үшін
тер үшін 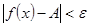 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда 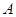 саны
саны  функциясының
функциясының 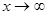 шегі деп аталады және
шегі деп аталады және 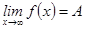 түрінде белгіленеді.
түрінде белгіленеді.
Ескерту: Жоғарыдағы анықтамалардан  функциясы ретімен алғанда
функциясы ретімен алғанда 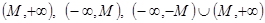 интервалдарында анықталады деп есептеледі. Дербес жағдайда, егер
интервалдарында анықталады деп есептеледі. Дербес жағдайда, егер  функциясы
функциясы 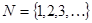 натурал сандар жиынында да анықталса, онда
натурал сандар жиынында да анықталса, онда
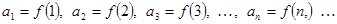
Белгілеулері 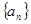 сан тізбегін анықтайды. Ал
сан тізбегін анықтайды. Ал 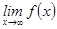 өрнегі былайша
өрнегі былайша 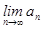 сан тізбегі шегіне көшеді. Функцияның нүктедегі және ақырсыздықтағы шектерін шартты түрде
сан тізбегі шегіне көшеді. Функцияның нүктедегі және ақырсыздықтағы шектерін шартты түрде 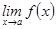 (
( 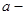 сан немесе
сан немесе 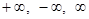 шексіздіктерінің біреуі) етіп белгілейік. Онда функция шегінің қасиеттері мен тізбектер шегінің қасиеттері бірдей болады. Мысалы:
шексіздіктерінің біреуі) етіп белгілейік. Онда функция шегінің қасиеттері мен тізбектер шегінің қасиеттері бірдей болады. Мысалы:
1) Тұрақты функцияның (тізбектің) шегі осы тұрақтыға тең,
2) Егер функцияның (тізбектің) шегі болса, онда ол жалғыз болады.
Анықтама.  функциясы
функциясы 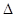 жиынында анықталып,
жиынында анықталып, 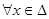 үшін
үшін 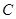 саны табылып,
саны табылып, 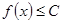 (
( 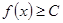 ) теңсіздігі орындалса, онда
) теңсіздігі орындалса, онда  функциясы
функциясы 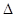 жиынында жоғарыдан (төменнен) шектелген делінеді. Функция жоғарыдан (төменнен) шектелсе, онда ол
жиынында жоғарыдан (төменнен) шектелген делінеді. Функция жоғарыдан (төменнен) шектелсе, онда ол 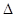 аралығында шектеулі. Мысалы,
аралығында шектеулі. Мысалы,
а) 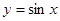 функциясы
функциясы 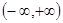 аралығында шектеулі, себебі кезкелген
аралығында шектеулі, себебі кезкелген 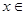
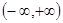 үшін
үшін 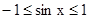 ;
;
б) 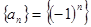 тізбегі шектеулі.
тізбегі шектеулі. 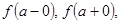
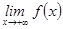 ,
, 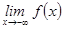 шектері бар болғанда, функция
шектері бар болғанда, функция 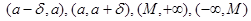 интервалдарында шектеулі.
интервалдарында шектеулі.
в) 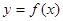 функциясы a нүктесінің маңайында шектеулі.
функциясы a нүктесінің маңайында шектеулі.
г) Шегі бар кезкелген сан тізбегі шектеулі.
Теорема. (а, 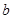 ) интервалында функция өспелі (кемімелі) болса және осы аралықта жоғарыдан (төменнен) С санымен шектелсе, онда
) интервалында функция өспелі (кемімелі) болса және осы аралықта жоғарыдан (төменнен) С санымен шектелсе, онда 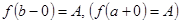 , яғни функцияның
, яғни функцияның 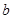 нүктесінде сол жақ (
нүктесінде сол жақ ( 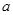 нүктесінде оң жақ) шегі табылады және
нүктесінде оң жақ) шегі табылады және 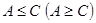 .
.
Жаттығу: Бұл теореманы сан тізбегі үшін келтіріңіз.
Шексіз аз және шексіз үлкен функциялар.
Анықтама. Егер 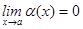 болса, онда теңдігі орындалса, онда
болса, онда теңдігі орындалса, онда 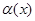 функциясы
функциясы 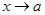 (
( 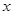 шамасы
шамасы 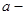 ға ұмтылғанда)шексіз аз шама (ш.а.ш.) деп аталады.
ға ұмтылғанда)шексіз аз шама (ш.а.ш.) деп аталады.
Анықтама. Егер 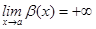 болса, онда
болса, онда 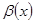 функциясы
функциясы 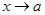 -ғы шексіз үлкен шама (ш.ү.ш.) деп атайды.
-ғы шексіз үлкен шама (ш.ү.ш.) деп атайды.
Теорема. Егер 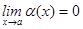 (ш.а.ш.) болса,
(ш.а.ш.) болса, 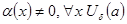 болса, онда
болса, онда 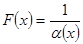 - функциясы
- функциясы 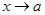 -ға ш.ү.ш. болады. Бұл теорема керісінше де ақиқат.
-ға ш.ү.ш. болады. Бұл теорема керісінше де ақиқат.
Шектер туралы негізгі теоремалар.Егер 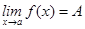 ,
, 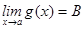 , болса, онда
, болса, онда
1. 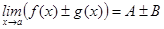
2. 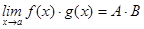
3.Кезкелген 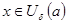 үшін,
үшін, 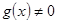 және
және 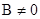 болса, онда
болса, онда 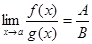 .
.
1-мысал. 1. 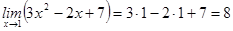 . Шекті есептеу үшін х-тің мәнін қойғанда
. Шекті есептеу үшін х-тің мәнін қойғанда 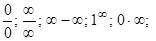 т.с.с. анықталмағандықтар пайда болады. Шекті есептеу деп осы анықталмағандықтарды ашуды айтады.
т.с.с. анықталмағандықтар пайда болады. Шекті есептеу деп осы анықталмағандықтарды ашуды айтады.
2. 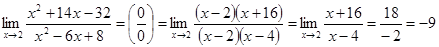 .
.
3. 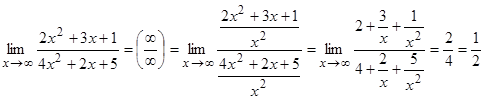 .
.
4. 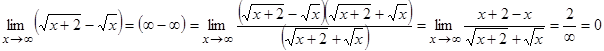 .
.
Әдебиеттер: нег.[128-163], [173-181], 11 қос. [314-334].
Бақылау сұрақтар:
1. Фукцияның анықтамасын беріңіз. Функцияның анықталу облысы дегеніміз не?
2. Тақ және жұп функциялардың анықтамасын беріңіз.
3. Период және периодты функциялар.
4. Функциялардың шектері туралы негізгі теоремаларды атаңыз.
Дәріс.
Дәріс тақырыбы:Бірінші және екінші тамаша шектер.
Дәріс жоспары:
§ Бірінші тамаша шек.
§ Екінші тамаша шек.
§ Шексіз аздарды салыстыру.
§ Функцияның үзіліссіздігі.
§ Кесіндіде үзіліссіз функцияның қасиеттері.
§ Әдебиеттер.
§ Бақылау сұрақтары.
Құрамында тригонометриялық функциялар бар өрнектердің шектерін есептегенде бірінші тамаша шекті қолданады: 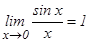 . Дәлелдеу: Радиусы бірге тең шеңбер аламыз.
. Дәлелдеу: Радиусы бірге тең шеңбер аламыз. 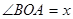 , сонда:
, сонда:
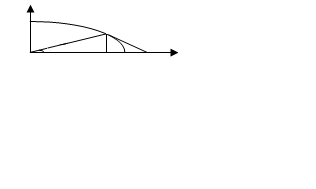
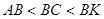 , мұндағы
, мұндағы
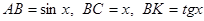
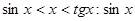
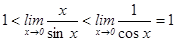
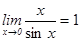
1-мысал. 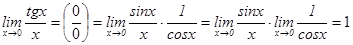
2-мысал. 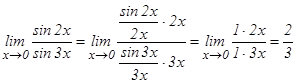 .
.
Екінші тамаша шек: .
Мұндағы е»2,718282… – иррационал сан.
3-мысал. Шекті есептеу керек
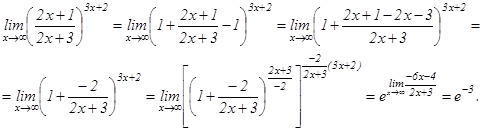
Шексіз аздарды салыстыру. Екі шексіз аз шамаларды салыстыру үшін олардың қатынасын қарастырады. 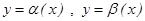 - ш.а.ш. болсын, яғни
- ш.а.ш. болсын, яғни 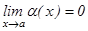 және
және 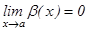 .
.
1. Егер 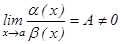 болса, онда
болса, онда 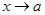 ұмтылғанда
ұмтылғанда 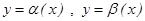 ш.а.ш.-ның аздық реттері бірдей дейді.
ш.а.ш.-ның аздық реттері бірдей дейді.
2. Егер 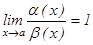 болса, онда
болса, онда 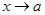 ұмтылғанда
ұмтылғанда 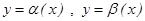 шексіз аз шамалар эквивалентті деп аталады және
шексіз аз шамалар эквивалентті деп аталады және 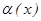 ~
~ 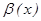 деп белгіленеді.
деп белгіленеді.
Мысал. 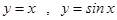 шексіз аздар
шексіз аздар 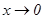 ұмтылғанда эквивалентті, бұл бірінші тамаша шектің қасиетінен шығады.
ұмтылғанда эквивалентті, бұл бірінші тамаша шектің қасиетінен шығады.
Теорема. 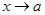 ұмтылғанда
ұмтылғанда 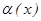 ш.а. болсын, онда:
ш.а. болсын, онда:
1. 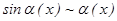 ; 2.
; 2. 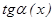 ~
~ 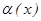 ;
;
3. 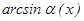 ~
~ 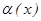 ; 4.
; 4. 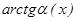 ~
~ 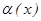 ;
;
5. 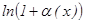 ~
~ 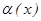 ; 6.
; 6. 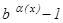 ~
~ 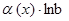 ,
, 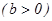 ;
;
Теорема. Егер ш.а.ф. –ды оларға эквивалентті функциялармен алмастырса, онда екі ш.а.ф. қатынасының шегі өзгермейді.
4-мысал. 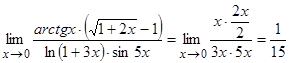 ,
,
себебi, 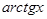 ~
~ 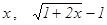 ~
~ 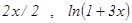 ~
~ 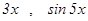 ~
~ 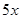 .
.
Функцияның үзіліссіздігі.Функцияның нүктедегі үзіліссіздігі ұғымын беру үшін 3 шартты келтіреміз:
1. 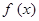 функциясы
функциясы 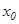 нүктесінде анықталған (яғни
нүктесінде анықталған (яғни 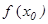 мәні бар);
мәні бар);
2. 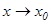 (
( 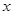 шамасы
шамасы 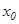 -ге ұмтылғанда) болғанда
-ге ұмтылғанда) болғанда 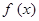 функциясының ақырлы шегі
функциясының ақырлы шегі 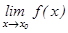 бар;
бар;
3. 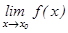 шегі функцияның
шегі функцияның 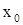 нүктесіндегі мәніне тең:
нүктесіндегі мәніне тең: 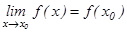
1−анықтама. Егер 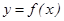 функциясы келтірілген үш шартты қанағаттандырса, онда оны
функциясы келтірілген үш шартты қанағаттандырса, онда оны 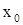 нүктесінде үзіліссіз дейді. Функцияның
нүктесінде үзіліссіз дейді. Функцияның 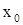 нүктесіндегі үзіліссіздігінің анықтамасының формуласын былай жазуға болады:
нүктесіндегі үзіліссіздігінің анықтамасының формуласын былай жазуға болады: 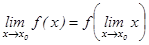 Функция
Функция 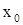 нүктесінде үзіліссіз болса, онда оның графигін
нүктесінде үзіліссіз болса, онда оның графигін 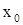 нүктесі арқылы үзіліссіз сызуға (қарындашты қағаздан алмай) болады. Енді үзіліссіздіктің екінші анықтамасын берейік.
нүктесі арқылы үзіліссіз сызуға (қарындашты қағаздан алмай) болады. Енді үзіліссіздіктің екінші анықтамасын берейік. 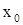 аргументіне
аргументіне 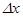 өсімшесін берсек,
өсімшесін берсек, 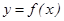 функциясы
функциясы 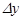 өсімшесін алады. Ол
өсімшесін алады. Ол 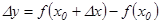 формуласымен анықталады.
формуласымен анықталады.
2−анықтама. Егер 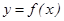 функциясы
функциясы 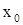 нүктесінде анықталса және
нүктесінде анықталса және 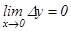 теңдігі орындалса, онда ол функцияны
теңдігі орындалса, онда ол функцияны 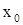 нүктесінде үзіліссіз дейді. Үзіліссіздіктің осы екі анықтамасы өзара эквивалентті. Егер
нүктесінде үзіліссіз дейді. Үзіліссіздіктің осы екі анықтамасы өзара эквивалентті. Егер 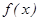 функциясы
функциясы 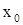 нүктесінде үзіліссіз болмаса, онда бұл нүкте
нүктесінде үзіліссіз болмаса, онда бұл нүкте 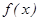 функциясының үзіліс нүктесі деп аталады. Үзіліс нүктесінің екі түрі бар. Егер
функциясының үзіліс нүктесі деп аталады. Үзіліс нүктесінің екі түрі бар. Егер 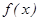 функциясың
функциясың 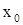 нүктесінде оң жақты және сол жақты шектері бар болып, бірақ олар өзара тең болмаса, онда
нүктесінде оң жақты және сол жақты шектері бар болып, бірақ олар өзара тең болмаса, онда 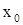 нүктесі
нүктесі 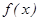 функциясының біріншітекті үзіліс нүктесі деп аталады. Егер оң жақты және сол жақты шектердің ең болмағанда біреуі не шексіздікке тең болып, не жоқ болса, онда
функциясының біріншітекті үзіліс нүктесі деп аталады. Егер оң жақты және сол жақты шектердің ең болмағанда біреуі не шексіздікке тең болып, не жоқ болса, онда 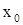 нүктесі
нүктесі 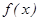 функциясының екіншітекті үзіліс нүктесі деп аталады. Егер
функциясының екіншітекті үзіліс нүктесі деп аталады. Егер 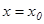 нүктесінде ақырлы оң жақты және сол жақты шектер бар болып, бірақ олар осы нүктедегі функцияның мәніне тең болмаса, онда
нүктесінде ақырлы оң жақты және сол жақты шектер бар болып, бірақ олар осы нүктедегі функцияның мәніне тең болмаса, онда 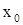 нүктесі
нүктесі 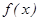 функциясының түзетілетін үзіліс нүктесі деп аталады.
функциясының түзетілетін үзіліс нүктесі деп аталады.
5-мысал. 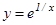 функциясы үшін
функциясы үшін 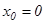 нүктесі екінші текті үзіліс нүктесі болады, себебі
нүктесі екінші текті үзіліс нүктесі болады, себебі
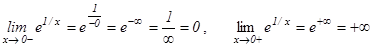
 |
Егер 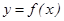 функциясы
функциясы 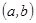 аралығының әрбір нүктесінде үзіліссіз болса, онда оны
аралығының әрбір нүктесінде үзіліссіз болса, онда оны 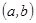 аралығында үзіліссіз дейді. Егер
аралығында үзіліссіз дейді. Егер 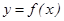 функциясы
функциясы 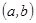 аралығында үзіліссіз болып, ал
аралығында үзіліссіз болып, ал 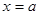 нүктесінде оң жақтан (яғни
нүктесінде оң жақтан (яғни 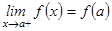 ), ал
), ал 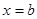 нүктесінде сол жақтан (яғни
нүктесінде сол жақтан (яғни 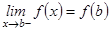 ) үзіліссіз болса, онда
) үзіліссіз болса, онда 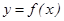 функциясын
функциясын 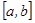 кесіндісінде үзіліссіз дейді.
кесіндісінде үзіліссіз дейді.
