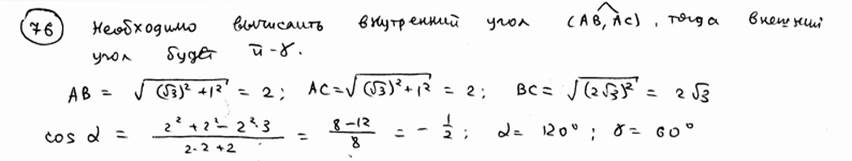| 44 | | Вычислить проекцию отрезка на ось u, если даны его длина d и угол j наклона к оси: | |
| | | 44.1 | d=6, j =p /3; |
| | | 44.2 | d=6, j =2p /3; |
| | | 44.3 | d=7, j =p /2; |
| | | 44.4 | d=5, j =0; |
| | | 44.5 | d=5, j =p ; |
| | | 44.6 | d=4, j = -p /3. 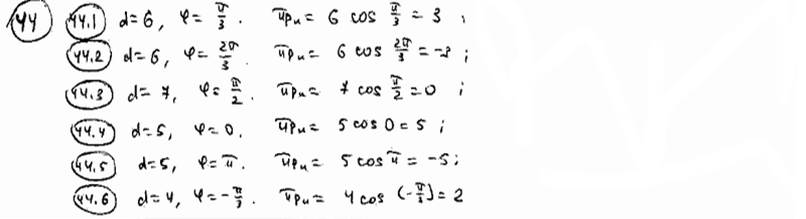 |
| | 45 | | Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на координатные оси: |
| | | 45.1 | X=3, Y=2; |
| | | 45.2 | X=2, Y=-5; |
| | | 45.3 | X=-5, Y=0; |
| | | 45.4 | X=-2, Y=3; |
| | | 45.5 | X=0, Y=3; |
| | | 45.6 | X=-5, Y=-1;  |
| | 46 | | Построить на чертеже отрезки, имеющие началом точку M(2; -1), зная их проекции на координатные оси: |
| | | 46.1 | X=4. Y=3; |
| | | 46.2 | X=2, Y=0; |
| | | 46.3 | X=-3, Y=1; |
| | | 46.4 | X=-4, Y=-2; |
| | | 46.5 | X=0, Y=-3; |
| | | 46.6 | X=1, Y=-3.  |
| | 47 | | Даны точки М1(1; -2), М2(2; 1), М3(5; 0), М4(-1; 4), М5(0; -3). Найти проекции на координатные оси следующих отрезков: |
| | | 47.1 | 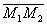 |
| | | 47.2 | 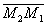 |
| | | 47.3 | 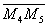 |
| | | 47.4 |   |
| | 48 | | Даны проекции X=5, Y=-5 отрезка 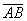 на координатные оси; зная, что его начало в точке М1(-2; 3), найти координаты его конца. на координатные оси; зная, что его начало в точке М1(-2; 3), найти координаты его конца.  |
| | 49 | | Даны проекции X=4, Y=-5 отрезка 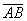 на координатные оси; зная, что его конец в точке B(1; -3), найти координаты его начала. на координатные оси; зная, что его конец в точке B(1; -3), найти координаты его начала.  |
| | 50 | | Построить на чертеже отрезки, исходящие оиз начала координат, зная длину d и полярный угол q каждого из них: |
| | | 50.1 | d=5, q =p /5; |
| | | 50.2 | d=3, q =5p /6; |
| | | 50.3 | d=4, q =-p /3; |
| | | 50.4 | d=3, q =-4p /3.  |
| | 51 | | Построить на чертеже отрезки, имеющие началом точку М(2; 3), зная длину и полярный угол каждого из них (координаты точки М декартовы): |
| | | 51.1 | d=2, q =-p /10; |
| | | 51.2 | d=1, q =p /9; |
| | | 51.3 | d=5, q =-p /2ж 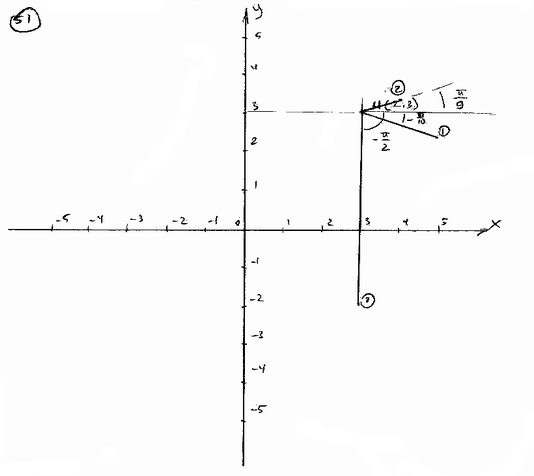 |
| | 52 | | Вычислить проекции на координатные оси отрезков, зная длину d и полярный угол q каждого из них: |
| | | 52.1 | d=12, q =2p /3; |
| | | 52.2 | d=6, q =-p /6; |
| | | 52.3 | d=2, q =-p /4.  |
| | 53 | | Даны проекции отрезков на координатные оси. Вычислить длину каждого из них. |
| | | 53.1 | X=3, Y=-4; |
| | | 53.2 | X=12, Y=5; |
| | | 53.3 | X=-8, Y=6.  |
| | 54 | | Даны проекции отрезков на координатные оси. Вычислить длину d и полярный угол q каждого из них. |
| | | 54.1 | X=1, Y= 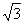 ; ; |
| | | 54.2 | X= 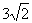 , Y= , Y=  ; ; |
| | | 54.3 | X= 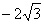 , Y=2. , Y=2.  |
| | 55 | | Даны точки М1(2; -3), M2(1; -4), M3(-1; -7), M4(-4; 8). Вычислить длину и полярный угол слдующих отрезков: |
| | | 55.1 | 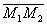 |
| | | 55.2 | 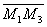 |
| | | 55.3 | 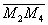 |
| | | 55.4 |   |
| | 56 | | Длина d отрезка равна 5, его проекция на ось абсцисс равна 4. Найти проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат: |
| | | 56.1 | Острый угол; |
| | | 56.2 | Тупой угол.  |
| | 57 | | Длина отрезка 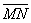 равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна –12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат: равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна –12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат: |
| | | 57.1 | Острый угол; |
| | | 57.2 | Тупой угол. 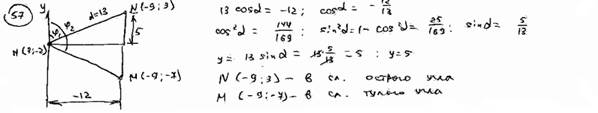 |
| | 58 | | Длина отрезка 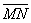 равна 17, его конец в точке N(-7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс: равна 17, его конец в точке N(-7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс: |
| | | 58.1 | Острый угол; |
| | | 58.2 | Тупой угол.  |
| | 59 | | Зная проекции X=1, Y= 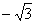 отрезка на координатные оси, найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3. отрезка на координатные оси, найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3.  |
| | 60 | | Даны две точки M1(1; -5), M2(4; -1). Найти проекцию отрезка 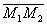 на ось, которая составляет с осью Ox угол q =-p /6. на ось, которая составляет с осью Ox угол q =-p /6. 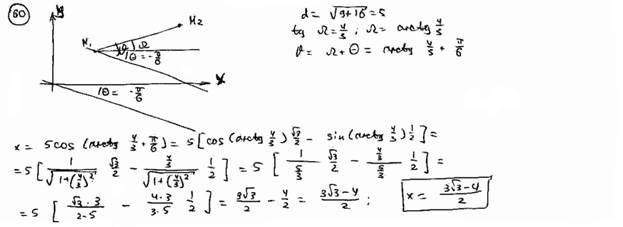 |
| | 61 | | Даны две точки P(-5; 2), Q(3; 1). Найти проекцию отрезка 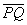 на ось, которая составляет с осью Ox угол на ось, которая составляет с осью Ox угол 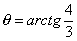  |
| | 62 | | Даны две точки M1(2; -2), M2(7; -3). Найти проекцию отрезка 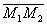 на ось, проходящую через точки A(5; -4), B(-7; 1) и направленную: на ось, проходящую через точки A(5; -4), B(-7; 1) и направленную: |
| | | 62.1 | от А к В; |
| | | 62.2 | от В к А.  |
| | 63 | | Даны точки A(0; 0), B(3; -4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d между точками: |
| | | 63.1 | А и В. |
| | | 63.2 | В и С. |
| | | 63.3 | А и С. |
| | | 63.4 | C и D. |
| | | 63.5 | A и D. |
| | | 63.6 | D и E.  |
| | 64 | | Даны две смежные вершины квадрата A(3; -7) и В(-1; 4). Вычислить его площадь. 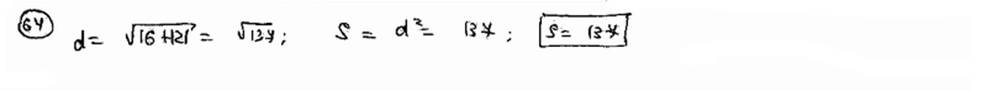 |
| | 65 | | Даны две противоположные вершины квадрата P(3; 5), Q(1; -3). Вычислить его площадь.  |
| | 66 | | Вычислить площадь правильного треугольника, две вершины которого суть A(-3; 2), B(1; 6). 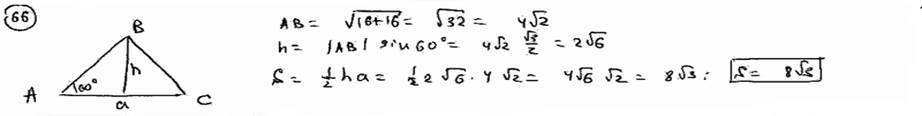 |
| | 67 | | Даны три вершины А(3; -7), В(5; -7), С(-2; 5) параллелограмма ABCD, четвертая вершина которого D противоположна B. Определить длины диагоналей того параллелограмма.  |
| | 68 | | Сторона ромба равна 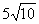 , две его противоположные вершины суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого ромба. , две его противоположные вершины суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого ромба.  |
| | 69 | | Сторона ромба равна 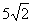 , две его противоположные вершины суть точки P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба. , две его противоположные вершины суть точки P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба.  |
| | 70 | | Доказать, что точки А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.  |
| | 71 | | Доказать, что треугольник с вершинами A1(1; 1), A2(2; 3), A3(5; -1) прямоугольный. 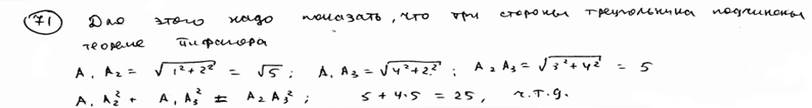 |
| | 72 | | Доказать, что точки А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами квадрата. 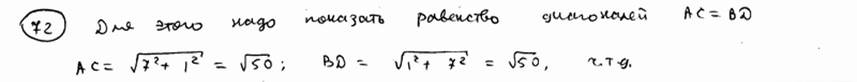 |
| | 73 | | Определить, есть ли среди внутренних углов треугольника с вершинами M1(1; 1), M2(0; 2), M3(2; -1) тупой угол.  |
| | 74 | | Доказать, что все внутренние углы треугольника с вершинами M(-1; 3), N(1; 2), P(0, 4) острые. 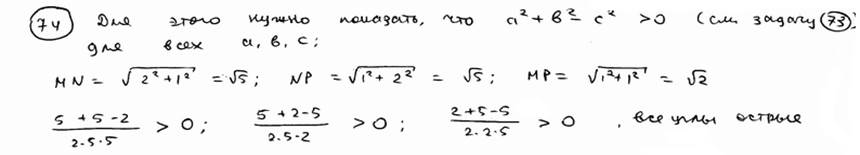 |
| | 75 | | Вершины треугольника суть точки A(5; 0), B(0; 1), C(3; 3). Вычислить его внутренние углы.  |
| | 76 | | Вершины треугольника суть точки А( 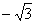 ; 1), B(0, 2), C( ; 1), B(0, 2), C( 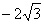 ; 2). Вычислить его внешний угол при вершине А. ; 2). Вычислить его внешний угол при вершине А. 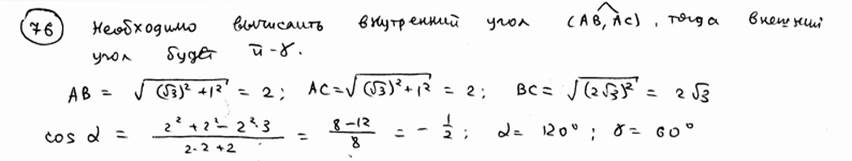 |
| | 77 | | На оси абсцисс найти такую точку М, расстояние от которой до точки N(2; -3) равнялось бы 5.  |
| | 78 | | На оси ординат найти такую точку М, расстояние от которой до точки N(-8; 13 равнялось бы 17.  |
| | 79 | | Даны две точки M(2; 2), N(5; -2); на оси абсцисс найти такую точку Р, чтобы угол MPN был прямым.  |
| | 80 | | Через точку А(4; 2) проведена окружность, касающаяся обеих координатных осей. Определить ее центр С и радиус R.  |
| | 81 | | Через точку М1(1; -2) проведена окружность радиуса 5, касающаяся оси Ox. Определить центр С окружности.  |
| | 82 | | Определить координаты точки М2, симметричной точке М1(1; 2) относительно прямой, проходящей через точки А(1; 0), В(-1; -2).  |
| | 83 | | Даны две противоположные вершины квадрата А(3; 0) и С(-4; 1). Найти две его другие вершины.  |
| | 84 | | Даны две смежные веришны квадрата А(2; -1) и В(-1; 3). Определить две его другие вершины. 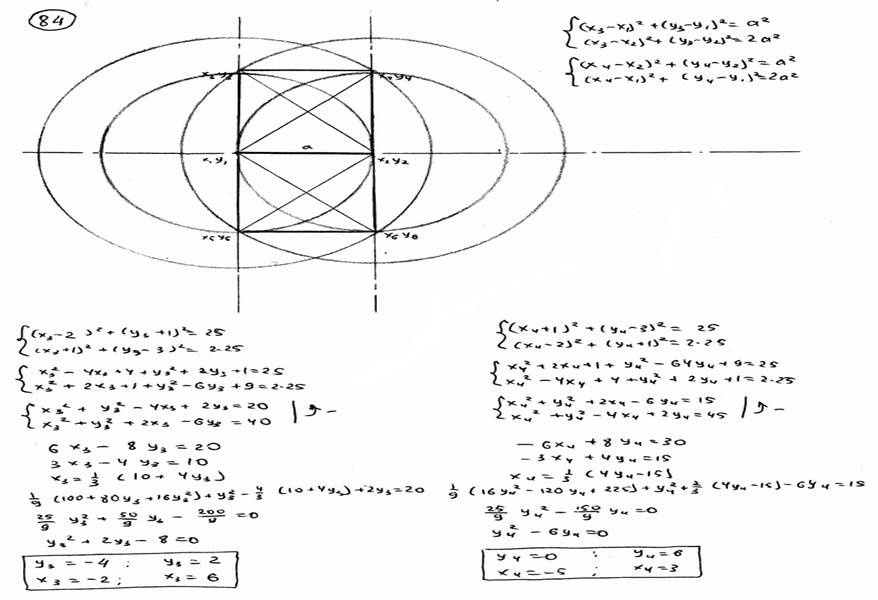 |
| | 85 | | Даны вершины треугольника M1(-3; 6), M2(9; -10), M3(-5; 4). Определить центр С и радиус R круга, описанного около этого треугольника.  |
| | | | | | | |
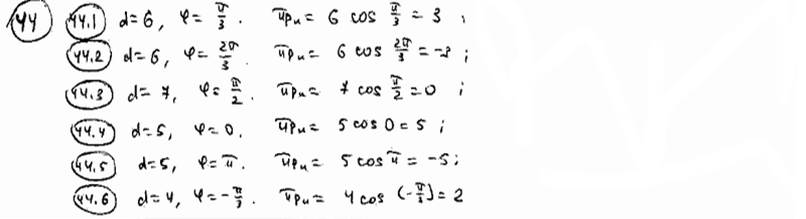


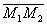
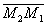
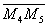


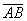 на координатные оси; зная, что его начало в точке М1(-2; 3), найти координаты его конца.
на координатные оси; зная, что его начало в точке М1(-2; 3), найти координаты его конца. 
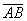 на координатные оси; зная, что его конец в точке B(1; -3), найти координаты его начала.
на координатные оси; зная, что его конец в точке B(1; -3), найти координаты его начала. 




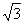 ;
; 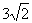 , Y=
, Y=  ;
; 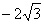 , Y=2.
, Y=2. 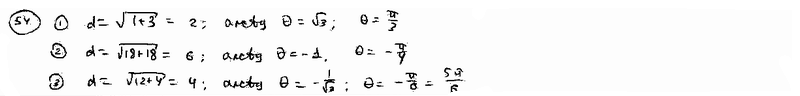
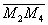



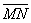 равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна –12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат:
равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна –12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат: 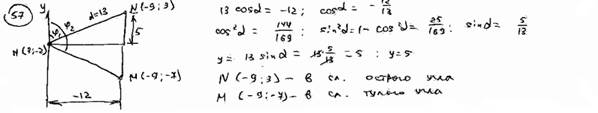
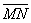 равна 17, его конец в точке N(-7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс:
равна 17, его конец в точке N(-7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс: 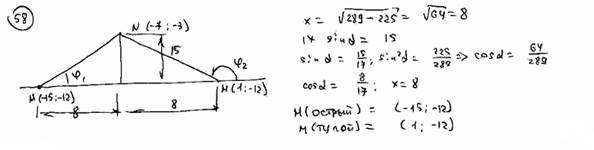
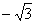 отрезка на координатные оси, найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3.
отрезка на координатные оси, найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3. 
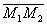 на ось, которая составляет с осью Ox угол q =-p /6.
на ось, которая составляет с осью Ox угол q =-p /6. 
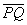 на ось, которая составляет с осью Ox угол
на ось, которая составляет с осью Ox угол 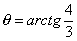

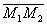 на ось, проходящую через точки A(5; -4), B(-7; 1) и направленную:
на ось, проходящую через точки A(5; -4), B(-7; 1) и направленную: 

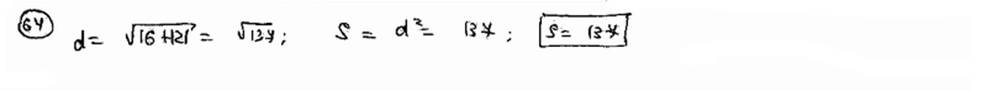

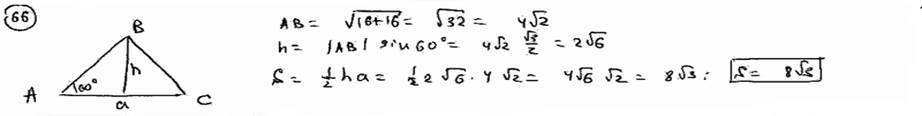

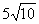 , две его противоположные вершины суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого ромба.
, две его противоположные вершины суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого ромба. 
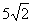 , две его противоположные вершины суть точки P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба.
, две его противоположные вершины суть точки P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба. 

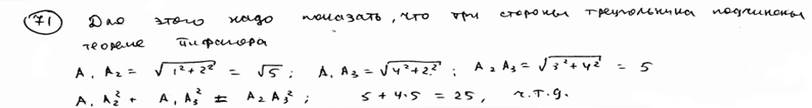
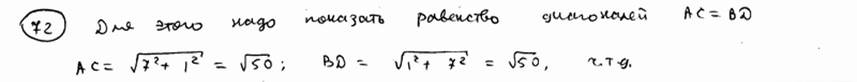

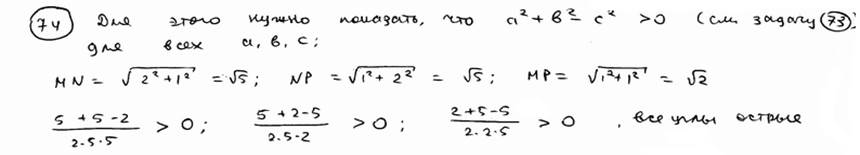

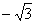 ; 1), B(0, 2), C(
; 1), B(0, 2), C( 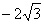 ; 2). Вычислить его внешний угол при вершине А.
; 2). Вычислить его внешний угол при вершине А.