Прискорення швидкості збіжності

Ефективність методів простої ітерації і ітерації Зайделя можна набагато підвищити за рахунок застосування спеціальних способів прискорення швидкості збіжності обчислювального процесу.

Виконують лінійне прискорення збіжності. Суть його полягає в тому, що на k+1- кроці після визначення 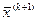за звичайними формулами обчислюють його поліпшене значення:

,

де 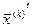- поліпшене значення попереднього кроку, α – коефіцієнт прискорення, який лежить у межах 1...2.

Як показує практика, під час розв’язування рівнянь усталених електромагнітних режимів ЕЕС, коефіцієнт прискорення для уявних складових координат режиму слід дати на 20%÷30% більшим від коефіцієнта для дійсних складових. Оптимальне значення коефіцієнта прискорення для дійсних складових режиму лежить у межах 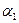=1,2... 1,6 ; для уявних – 1,6... 1,8.

Коефіцієнт прискорення слід вводити не на перших кроках, а приблизно тоді, коли процес ітерації стане монотонним, без стрибкоподібних змін невідомих.

Застосувавши лінійне прискорення ітерацій Зайделя, кількість кроків, що необхідні для досягнення належної точності, грубо можна оцінити кількість рівнянь системи.

І все ж таки процеси простої ітерації вимагають великої кількості кроків наближень.

§ 5.2.4 Метод найшвидшого спуску

Нехай рівняння 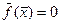(1) неперервне і має неперервні похідні в колі його визначення. Обчислення коренів рівняння зводиться до знаходження мінімуму скалярної функції:

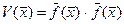. (2)

Задача розв’язання рівняння (1) зводиться до знаходження нульового мінімуму функції (2) у багатомірному просторі координат .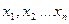

Формула скалярної функції (2):

,

де 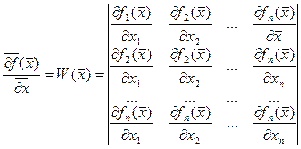– матриця Якобі.

Вектор ортогональний до поверхні рівня функції 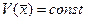і його напрям відповідає напряму найшвидшого зростання 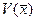. Рухаючись протилежно до напряму градієнта, переміщаємось до мінімуму функції 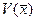, тобто можемо визначити вектор-корінь рівняння (1).

Методи, що ґрунтуються на такому підході, називаються градієнтними.

Якщо відоме наближене розміщення нульового мінімуму, тобто відоме деяке грубе (нульове) наближення розв’язку (1) 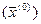, то, обчисливши 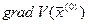, можна провести через точку 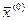пряму, протилежну до напрямку градієнта – в напрямі мінімуму функції 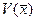, ідучи по цій прямій потрапляємо на поверхню мінімального в даному напрямі рівня у деякій точці . Далі відправляючись з точки , проти здійснюємо подібний рух до точки поверхні нового мінімального рівня 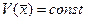і т.д. аж до точки нульової мінімальної функції .

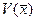Ламану лінію, по якій іде переміщення з точки х до мінімуму 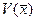, називають лінією найшвидшого спуску, а відповідний такому переміщенню градієнтний метод – методом найшвидшого спуску, або оптимальним градієнтний методом.

Для лінійного матрично-векторного рівняння (1):

Обчислення k є першого наближення розв’язку такого рівняння сформулюємо у вигляді алгоритму:

1) за знайденим на попередньому k-му кроці наближення 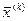одержуємо багатомірний вектор нев’язок:

;

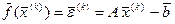2) обчислюємо вектор:

;

3) визначаємо вектор:

;

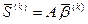4) шукаємо параметр ітерації:

;

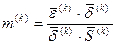5) знаходимо наступне (k+1) уточнення невідомого вектора :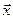

.

Точність розв’язання оцінюється Евклідовою нормою багатомірного вектора нев’язок :

· .

Розрахунок закінчиться при досягненні 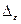бажаного значення.

§ 5.3. Чисельні методи розв’язування систем нелінійних рівнянь

§ 5.3.1Метод простої ітерації

Для розв’язування рівняння f(x)=0 запишемо у вигляді:

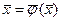(1) або 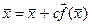, (2)

де с – деяка квадратна матриця.

З (1) і (2) знайдемо:

.

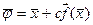Якщо f(x) має похідну в деякій області G, то знаходимо:

.

Достатньою умовою збіжності процесу ітерації в цій області є умова:

,

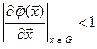де норма розглядається в сенсі ℓ - або m – норми.

Умова повинна задовольнятися на всіх кроках послідовних наближень, починаючи від .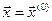

Матрицю с вибирають так, щоб:

чи (*)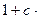

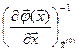Для нелінійних систем рівнянь:

.

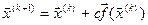Ітераційний процес збігається з швидкістю геометричної прогресії, що визначається з співвідношення:

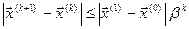, (3)

де .

Тут розглядається максимальне значення ℓ - або m – норми в області G при значенні вектора 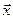, який він набирає у процесі ітерації.

Оцінка точності вектор-кореня на k-му кроці обчислень:

, (4)

де 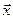- точне значення вектор-кореня.

В (3) і (4) норми визначаються в сенсі ℓ - або m – норми.

Необхідною і достатньою умовою збіжності простого ітераційного процесу є умова:

,

де λ – вектор власних значень матриці Якобі.

§ 5.3.2Метод ітерації Зайделя.

Подібно як в лінійних системах значення наближених “молодших” невідомих, знайдених на даному кроці, використовуються для визначення “старших” при цьому ж кроці наближення.

Отже, одержуємо таку послідовність обчислень:

,

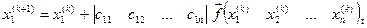
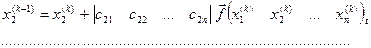де матриці рядки є відповідними рядками матриці с, яка визначається (*).

Всі операції (знаходження с і наближень) здійснюються так само, як і в простій ітерації.

§ 5.3.3 Метод найшвидшого спуску.

1) за одержаними на попередньому k-му кроці значеннями багатомірного вектора обчислюють багатомірний вектор відхилень (нев’язок): ;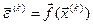

2) багатомірний вектор: ;

3) вектор: ;

4) параметр ітерації: ;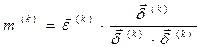

5) знайти наступне k+1-ше наближення невідомого багатомірного вектора: .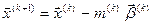

Метод градієнта в застосуванні до системи нелінійних рівнянь подібно як у випадку лінійних систем забезпечує абсолютну збіжність до мінімуму функції 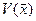. Якщо цей мінімум нульовий, то дістаємо розв’язок системи умови та швидкості збіжності на кроці ітерації, визначений так само, як і для системи лінійних рівнянь.

Розділ 6. Математичні основи методів аналізу перехідних процесів електроенергетичної системи

Перехідні процеси відповідають узагальненому стану систем і вони описуються диференційними (чи інтегрально-диференційними) та скінченими рівняннями.

У класичному варіанті задача аналізу перехідного процесу ЕЕС з математичного погляду зводиться до формування та розв’язування диференційних і скінчених рівнянь її стану.

Електромагнітні і електромеханічні явища ЕЕС та їхніх елементів у загальному випадку описуються системами нелінійних інтегрально-диференційних і скінчених рівнянь.

У найпростішому випадку, коли не враховуються залежності параметрів елементів систем від інтенсивності процесів, ці рівняння лінійні з постійними коефіцієнтами за умови, що параметри незмінні в часі, та зі змінними коефіцієнтами, якщо параметри елементів є функціями часу.

Здебільшого під час аналізу електроенергетичних систем, особливо при глибоких збуреннях і їхніх режимів, необхідно враховувати залежність параметрів системи від інтенсивності процесів і стан систем, тим самим описується нелінійними скінченими та диференційними рівняннями.

Під час аналізу ЕЕС та їх елементів основні дві задачі:

1) визначення кількісних характеристик явищ, точніше встановлення за тою чи іншою формою (аналітичною, числовою чи графічною) залежностей їх фізичних величин від координат простору і часу;

2) вивчення якісної сторони – як стійкості режимів ЕЕС.

Перша задача в математичному розумінні у загальному випадку зводиться до розв’язування скінчених і диференційних рівнянь (задача Коші чи крайова задача).

Другу задачу з математичного боку можна охарактеризувати як задачу оцінки стійкості розв’язання скінчених і диференційних рівнянь стану. При цьому, якщо розглядаються неглибокі збурення системи, задача часто розв’язується шляхом лінеаризації його диференційних рівнянь, які під час дослідження стійкості – нелінійні.

Загальним випадком звичайних диференційних рівнянь є система рівнянь першого порядку, яку можна записати у вигляді неявного матрично-векторного рівняння:

,

де 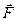- вектор-функція від вектора змінних , його похідних по аргументу х і самого аргументу.

В явному вигляді:

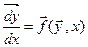— нормальна форма Коші.

Методи розв’язування диференційних рівнянь – точні й наближені.

Точні – це аналітичні, які дають алгоритм розв’язування зі строго визначеним числом кроків при виконанні абсолютно точних обчислень. Загальні точні розв’язання існують тільки для лінійних диференційних рівнянь у звичайних похідних.

До наближених відносяться наближені аналітичні методи, графічні та чисельні.

Аналітичні методи наближеного інтегрування диференційних рівнянь вимагають застосування квадратур, що часто не виражаються в елементарних функціях і не задовольняють вимог точності, компактності та оглядності розв’язань:

- інтегрування диференційних рівнянь за допомогою ступеневих рядів;

- метод послідовних наближень (метод Пікара) нагадує метод простої ітерації;

- метод малого параметра.

Графічні методи дуже обмежені щодо кола задач,0 оскільки їхні алгоритми вузькоспеціалізовані й не можуть задовольнити точності.

Широке застосування мають чисельні методи, які забезпечують розв’язування практично всіх задач інтегрування диференційних рівнянь з заданою точністю і є основними методами розв’язування диференційних рівнянь, аналізу, синтезу та керування ЕЕС і їх підсистем.

Суть чисельних методів інтегрування диференційних рівнянь, які часто називаються чисельними методами аналізу, полягає в послідовному обчисленні наближених значень інтегральної вектор-функції 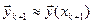на множині точок аргументу 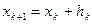, k=0,1..., n в інтервалі визначення вектор-функції при . Величину 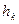називають кроком інтегрування.

Чисельні методи аналізу поділяються на однокрокові, багатокрокові, а також на явні та неявні.

В одно крокових методах наступне дискретне значення вектор-функції 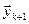визначається з використаного значення цієї ж вектор-функції тільки в одній попередній точці – k-ій ( ).

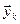У багатокрокових використовується значення вектор-функції в декількох попередніх точках (тобто 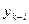при і = 0, 1, 2... n).

В явних методах здійснюється пряме обчислення інтегральної вектор-функції у вигляді:

.

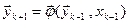У неявних – таке обчислення здійснюється на основі неявних скінчених рівнянь вигляду =0, що одержуються з диференційних рівнянь.

1. Як записують в загальному вигляді диференціальне рівняння за формою задачі Коші?

2. Які переваги має форма задачі Коші для розв'язування диференціального рівняння?

3. Які електричні величини відіграють роль змінних стану для електричних систем?

4. Які переваги має метод змінних стану в порівнянні з методами контурних струмів та вузлових напруг?

5. Охарактеризуйте суть перетворень повної системи рівнянь електричної системи до форми рівнянь змінних стану.

6. Як повинні бути замінені резистивні струми і напруги для одержання рівнянь за змінними стану?

7. Поясніть застосування методу суперпозиції для формування рівнянь змінних стану. Наведіть приклад для простої електричної системи.

8. Які матричні співвідношення дозволяють отримати рівняння для змінних стану?

9. Як можна за допомогою сигнальних графів отримати рівняння для змінних стану?

10. Як можна перетворити рівняння змінних стану до рівнянь з постійними або синусоїдними джерелами електричної енергії?

11. Поясніть геометричну суть однокрокових методів чисельного інтегрування диференціальних рівнянь.

12. Як визначають порядок методу чисельного інтегрування диференціальних рівнянь?

13. Які фактори зумовлюють похибку в процесі чисельного інтегрування диференціальних рівнянь?

14. Від яких факторів залежить стійкість чисельних методів інтегрування диференціальних рівнянь? Наведіть приклад прояву чисельної нестійкості.

15. У чому полягає суть неявних методів інтегрування диференціальних рівнянь. Які переваги вони мають перед явними методами?

16. Як можна виразити для лінійної електричної системи рівняння для змінних стану?

17. Що являє собою системна матриця, які способи її обчислення можна застосувати?

18. Поясніть суть системних методів чисельного інтегрування диференціальних рівнянь за методикою Ракитського‑Демірчана?

19. Опишіть алгоритм автоматизованого формування систем рівнянь за методом змінних стану.

20. У чому суть кусково-лінійної апроксимації нелінійних характеристик електричних двополюсників?

21. Як застосовують метод припасовування для аналізу динаміки нелінійних систем перетворення електричної енергії?

22. Поясніть алгоритми уточнення моментів перемикання напівпровідникових діодів та тиристорів при аналізі динамічних режимів електричних систем перетворення електроенергії.

Екзаменаційні запитання

1. Цілі і задачі курсу.

2. Особливості методів розглядуваних в курсі.

3. Застосування методів.

4. Структурні елементи електричного кола.

5. Аналітичний запис структури електричного кола.

6. Основні закони електричного кола.

7. Основні закони електричного кола в координатах струмів.

8. Основні закони електричного кола в координатах напруг.

9. Метод незалежних струмів.

10. Метод контурних струмів.

11. Метод незалежних напруг.

12. Метод вузлових напруг.

13. Матриці вхідних і взаємних адмітансів.

14. Матриця коефіцієнтів розподілу.

15. Матриця вузлових імпедансів.

16. Визначення подій і взаємозв’язки між ними.

17. Розрахунок імовірностей.

18. Основні теореми теорій імовірностей: теореми додавання; мно­ження імовірностей; формула повної імовірності; теорема гіпотез; повторення дослідів.

19. Випадкові величини в енергетиці.

20. Способи задання законів розподілу: ряд, функція і густина розподілу випадкової величини і їх властивості.

21. Закони розподілів випадкових величин.

22. Числові характеристики випадкових величин і їх властивості: математичне сподівання, дисперсія, середньо-квадратичне відхилення.

23. Поняття моменту випадкової величини.

24. Числові характеристики випадкових величин, розподілених за рівномірним законом розподілу.

25. Числові характеристики випадкових величин, розподілених за нормальним законом розподілу.

26. Числові характеристики випадкових величин, розподілених за біноміальним законом розподілу.

27. Числові характеристики випадкових величин, розподілених за законом розподілу Пуассона.

28. Поняття системи випадкових величин.

29. Функція і густи­на розподілу системи випадкових величин і їх властивості.

30. Функція і гус­тина розподілу окремих компонент системи випадкових величин.

31. Числові характеристики системи випадкових величин.

32. Кореляційний момент та коефіцієнт кореляції системи випадкових величин та їх властивості.

33. Умовне мате­матичне сподівання.

34. Математична статистика. Основні поняття.

35. Первинна статистична сукуп­ність і її впорядкування.

36. Згрупований статис­тичний ряд.

37. Гістограма.

38. Вирівнювання статис­тичних законів.

39. Критерії згоди Пірсона (χ²).

40. Критерії згоди Смірнова- Колмогорова.

41. Критерії згоди Колмогорова.

42. Довірчий інтервал і надійність.

43. Довірчий інтервал для математичного сподівання.

44. Довірчий інтервал для середньоквадратичного відхилення.

45. Оцінка істинного значення вимі­рюваної величини і точності вимірювань.

46. Оцінка числових характеристик випадкового вектора по обмеженому числу дослідів.

47. Статистики числових характеристик.

48. Побудова функції лінійної регресії.

49. Поняття випадкового процесу.

50. Закони розподілу і основні характеристики випадкового процесу.

51. Визначення з досліду числових характеристик випадкового процесу.

52. Поняття стаціонарності та ергодичності випадкового процесу.

53. Визначення з досліду числових характеристик стаціонарного випадкового процесу.

54. Визначення з досліду числових характеристик ергодичного стаціонарного процесу по одній реалізації.

55. Визначення з досліду числових характеристик нестаціонарного випадкового процесу по одній реалізації.

56. Теорія надійності. Основні положення.

57. Статистичні характерис­тики надійності.

58. Визначення надійності сис­теми на основі характеристики надійності її елементів.

Список рекомендованої літератури

1. Давиденко Л.В. Формалізовані методи аналізу електричних кіл. Програма та методичні вказівки до виконання розрахунково-графічних та контрольних робіт з курсу “Математичні задачі електроенергетики” для студентів спеціальності 6.090600 „Електротехнічні системи електроспоживання” всіх форм навчання. – Луцьк: ЛДТУ, 1998.

2. Давиденко Л. В. Матеметаична статистика. Методичні вказівки до практичних занять з курсу „Математичні задачі електроенергетики” для студентів спеціальності 6.090600 „Електротехнічні системи електроспоживання” всіх форм навчання. – Луцьк: ЛДТУ, 2001.

3. Давиденко Л.В. Конспект лекцій з дисципліни „Математичні задачі електроенергетики” для студентів спеціальності 6.090600 „Електротехнічні системи електроспоживання всіх форм навчання. – Луцьк: ЛДТУ, 2003.

3.Перхач В.С. Математичні задачі електроенергетики.- Львів: Вища шк.., 1989.

4. Математическая статистика /Иванова В.М., Калинина В.Н., Нешумова Л.А. и др.-М.: Высш. шк., 1981.

5. Р. Шторм. Теория вероятностей. Математическая статистика. Статистический контроль качества. – М.: Мир, 1970.

6. Сборник задач по теории вероятностей, математческой статистике и теории случайных функций / Под.рец. А.Л.Свешникова – Изд-во “Наука", Гл. ред. физ.-мат лит. 1970.

7. Электрические сети и системы: Математические задачи элетроэнергетики/ Под ред. Веникова В.А.- М.: Энергоатомиздат, 1988.

8. Элетрические сети и системы/ Н.В.Буслова, В.Н.Винославский, Г.Н.Денисенко, В.С.Перхач – К.: Высш.шк., 1986.

9. Е.С.Вентцель, Л.А.Овчаров. Теория вероятностей и ее инженерные приложения.-М.:Наука, Гл.ред.физ.-мат.лит., І988.

10. Блажкевич Б.І. Основні методи аналізу електричних кіл. – К.: Техніка, 1971.

11. Пугачев В.С. Теория случайных функцій. – М.: Физматтиз, 1960.