Матрично-топологические методы
После перехода от реальной физической системы к моделирующей ее электрической цепи, а от последней к схеме замещения, составленной из элементов базового набора, задача анализа заключается в нахождении токов и напряжений в каждом элементе, исходя из которых определяются все остальные необходимые характеристики схемы в целом.
При анализе схем с помощью ЭВМ (машинном анализе) в машину вводится информация, содержащая табличное описание схемы (перечень элементов, их параметры и способ соединения), режим анализа (статический, динамический) и перечень характеристик, подлежащих определению. Программа должна обеспечивать автоматизацию процессов анализа конфигурации схемы, составление системы линейно-независимых уравнений цепей, их решение в требуемых режимах и вывод результатов анализа.
Указанные задачи решаются с помощью матрично-топологических методов, основанных на теории графов и матричной алгебре. Конфигурация схемы представляется с помощью топологических матриц, на основании которых составляются векторно-матричные уравнения цепей. Параметры элементов схем представляют в виде параметрических матриц, которые используются для составления матричных уравнений, отражающих соотношения токов и напряжений элементов. Полученная система матричных уравнений решается соответствующими численными методами. В настоящем пособии разумеется не ставится задача подробного и математически строгого топологического машинного анализа, а скорее - введение в круг задач и формулировка основных понятий.
В основе топологических (геометрических) свойств цепей лежат два закона Кирхгофа, из которых видно, что топологические свойства цепей не зависят от тока и свойств элементов ее составляющих.
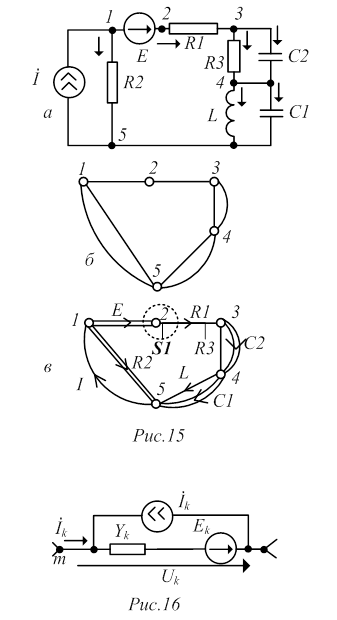
Если ветви электрической схемы (рис.15 а) заменить отрезками (дугами) произвольной длины и формы, а точки их соединений (узлы)-вершинами, т0 получившаяся геометрическая фигура (диаграмма) называется ненаправленным неориентированным графом электрических цепей (рис.15 б). Если на ветви графе нанести направления токов (напряжений) в вине стрелок, то получится ориентировочный, граф или орграф (рис. 15 в). Для удобства расчетов на ветвях орграфа указывают параметры в соответствии со схемой цепи (рис.15 в). Любую совокупность ветвей и вершин, принадлежащих графу, называют подграфом. Любой замкнутый путь, позволяющий выйти из вершины графа и вернуться в нее, не проходя дважды по одной ветви и не пересекая дважды одну и ту же вершину, называется контуром.
Подграф, содержаний все вершины графа и не содержащий ни одного контура, называется фундаментальным деревом графа, которое для краткости будет называться далее просто деревом (выделено двойными линиями на рис.15в).
Ветви графа, вошедшие в дерево, называются ветвями дерева или ребрами, а не вошедшие - хордами или ветвями связи. Совокупность хорд образует дополнение дерева. Если обозначить число вершин (узлов) графа через 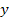 , число всех ветвей - через
, число всех ветвей - через 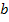 , число ребер - через р, а число хорд - через
, число ребер - через р, а число хорд - через 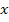 , то они связаны соотношениями:
, то они связаны соотношениями:
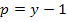
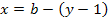
Для одного и того же графа можно построить много деревьев в зависимости от выбора начальной вершины. Часть из них будут изоморфными (отличаются только нумерацией вершин).
Граф схемы можно не только начертить, но и записать аналитически в виде таблицы, называемой матрицей соединений (инциденций). Число ее строк равно числу узлов (вершин графа), а число столбцов – числу ветвей. Каждый элемент 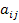 матрицы равен – I, если j-я ветвь входит в i-й узел, +I, если выходит 0 если она не соединена j-м узлом. Для получения линейно независимой системы вычеркивают одну из строк, обычно соответствующую базисному узлу, образующаяся при этом матрица A размером
матрицы равен – I, если j-я ветвь входит в i-й узел, +I, если выходит 0 если она не соединена j-м узлом. Для получения линейно независимой системы вычеркивают одну из строк, обычно соответствующую базисному узлу, образующаяся при этом матрица A размером 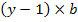 называется матрицей узлов. Общая структура матрицы A и ее содержание для графа на рис.15 (в) показаны в табл.4. Матрица A может быть представлена как совокупность подматриц:
называется матрицей узлов. Общая структура матрицы A и ее содержание для графа на рис.15 (в) показаны в табл.4. Матрица A может быть представлена как совокупность подматриц:
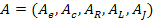
| Матрица A | ||||||||
| Подматрицы A | AE | AR | AC | AL | AJ | |||
| Ветви | E | R1 | R2 | R3 | C1 | C2 | L | J |
| Узел 1 Узел 2 Узел 3 Узел 4 | -I +I 0 0 | 0 -I +I 0 | -I 0 0 0 | 0 0 -I +I | 0 0 0 -I | 0 0 -I +I | 0 0 0 -I | +I 0 0 0 |
Кроме матрицы узлов , для описания топологии используют матрицы главных сечений и главных контуров. Сечением называется любая минимальная совокупность ветвей, при удалении которых граф распадается на два подграфа.; Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности Si , однократно рассекающей соответствующие ветви; часть графа, заключенную внутри сечения называют обобщенным узлом. Главным сечением называется сечение, одна из ветвей которого есть ребро, а остальные ветви-хорды (например сечение S1 , отмеченное пунктиром на рис.15 в). Главным контуром называется контур, образующийся при подключении хорды к дереву графа.
Очевидно, что число главных сечений равно числу pебep, т.е. 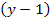 , а число главных контуров – числу хорд, т.е. b-y-1. Матрица главных сечений Q – это прямоугольная таблица размером
, а число главных контуров – числу хорд, т.е. b-y-1. Матрица главных сечений Q – это прямоугольная таблица размером 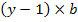 , строки которой соответствуют главным сечениям, а столбцы – ветвям графа. Каждый элемент qij этой матрицы равен +I, если j - я ветвь входит в i-е сечение со знаком «+», равен –I, если со знаком « - » и 0, если не входит; при этом за положительное направление ветви в сечении принимается направление ветви дерева этого сечения.
, строки которой соответствуют главным сечениям, а столбцы – ветвям графа. Каждый элемент qij этой матрицы равен +I, если j - я ветвь входит в i-е сечение со знаком «+», равен –I, если со знаком « - » и 0, если не входит; при этом за положительное направление ветви в сечении принимается направление ветви дерева этого сечения.
Матрицей главных контуров B называется таблица размеров 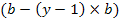 , строки котрой соответствуют главным контурам, а столбцы – ветвям графа. Каждый элемент bij этой матрицы равен + 1 , если направление ветви совпадает с направлением обхода контура, -1— при противоположном направлении и 0, если ветвь не входит в контур. За направление контура выбирают направление хорды (ветви связи) этого контура.
, строки котрой соответствуют главным контурам, а столбцы – ветвям графа. Каждый элемент bij этой матрицы равен + 1 , если направление ветви совпадает с направлением обхода контура, -1— при противоположном направлении и 0, если ветвь не входит в контур. За направление контура выбирают направление хорды (ветви связи) этого контура.
С помощью топологических матриц можно сформулировать законы Кирхгофа для электрических цепей в матричной форме. Обозначим через
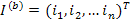
столбцовую матрицу токов всех ветвей, тогда уравнение
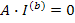
представляет матричную запись I-го закона Кирхгофа. Если обозначить через
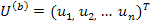
столбцовую матрицу напряжений ветвей, то уравнение
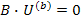
представляет матричную запись 2-го закона Кирхгофа. Соответственно уравнение
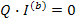
представляет запись 1-го закона Кирхгофа для обобщенных узлов. Если обобщенные узлы совпадают с простыми узлами схемы, то
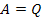
Дуальными называют два графа, если узловая матрица одного их них A1 равна контурной матрице B2 другого (и наоборот):
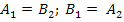
Отсюда следует свойства дуальности электрических схем и правила построения дуальных цепей, отмеченные ранее.
С помощью матрицы A можно выразить напряжение всех ветвей через потенциалы узлов, если ввести столбцовую матрицу потенциалов узлов
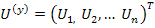
то
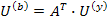
Где A – транспортировочная узловая матрица, а потенциалы узлов Ui отсчитываются относительно базисного угла. Если матрицу напряжений ветвей дерева обозначить через U(д), то
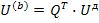
Т.е. напряжение любой ветви схемы можно определить через напряжение ветвей дерева.
Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разделена на две подматрицы:
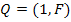
Где 1 – единичная подматрица порядка 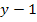 , столбцы которой соответствуют ветвям дерева; F – подматрица, столбцы которой соответствуют ветвям связи.
, столбцы которой соответствуют ветвям дерева; F – подматрица, столбцы которой соответствуют ветвям связи.
Токи всех ветвей могут быть выражены как линейные комбинации токов ветвей связи, можно вывести контурный ток, равный току ветви связи этого контура, тогда
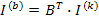
Где 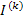 – столбцовая матрица контурных токов.
– столбцовая матрица контурных токов.
Если ветвям дерева присвоены первые номера, то матрица главных контуров состоит из двух подматриц:
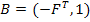
Следует подчеркнуть, что матрицы Q и B записаны для главных сечений и главных контуров, соответствующих одному и тому же дереву; единичные подматрицы в них имеют разный порядок: 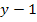 - в матрице Q и
- в матрице Q и 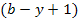 – в матрице B.
– в матрице B.
При практической решении задачи матрично-топологическими методами каждую ветвь K (рис.16) графа схемы представляют обобщенной ветвью, образованной двухполюсником Yk или
Zk и двумя источниками: напряжения Ėk и тока 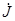 k . Тогда из закона Ома уравнение, описывающее эту ветвь будет иметь вид
k . Тогда из закона Ома уравнение, описывающее эту ветвь будет иметь вид
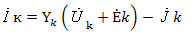
Используя уравнение
A·I=0
Находим
A·Y·U=A(J-Y·F)
И далее, подставляя
U=AT·U(y)
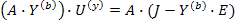
Назовем матрицей узловой проводимости
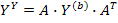
Тогда
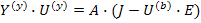
Узловое напряжение равно
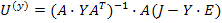
После того как найдено U(y) можно по уравнению найти U(b) и далее ток любой ветки 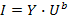 .
.
Проведенный анализ носит название узлового. Используя свойство дуальности можно провести контурный анализ. Из уравнения
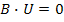
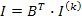
И уравнения обобщенной ветви в виде
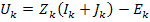
Получим
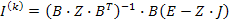
Это векторно-матричное уравнение относительно всех контурных токов (токов связей графа), представляющее собой в развернутом виде систему из 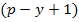 интегро-дифференциальных уравнений. При получении графа из схемы цепи требуется закорачивать источники напряжений и разрывать ветви с источниками тока, а ветви с идентичными источниками преобразовать специальными приемами или соблюдать приоритет (иерархию) формирования матриц по столбцам в виде правила
интегро-дифференциальных уравнений. При получении графа из схемы цепи требуется закорачивать источники напряжений и разрывать ветви с источниками тока, а ветви с идентичными источниками преобразовать специальными приемами или соблюдать приоритет (иерархию) формирования матриц по столбцам в виде правила
 Дерево
Дерево
 E, C, R, L, J
E, C, R, L, J
Дополнение
Таким образом, ветви с источниками напряжения должны быть в дереве графа, а с источниками тока - в его дополнении, т.е. являться хордами (см. рис.15 в и табл.4).
Матрица проводимости ветвей Y становится недиагональной, если в схеме имеются управляемые напряжением источники тока и при наличии индуктивных связей.
Полученные уравнения (25), (27) неудобны для численного решения и в случае линейных уравнений их сводят к системе линейных алгебраических уравнений с помощью преобразований Фурье или Лапласа.
При условии, если R, C, L - элементы являются нелинейными, зависящими от напряжений и токов в них, то их параметры выражаются частными производными соответствующих функций.
При анализе переходных характеристик численными методами решения уравнений вся длительность переходного процесса рассматривается состоящей из большого количества интервалов времени.
Основным недостатком рассмотренных методов анализа цепей является необходимость обращения параметрических матриц вида 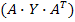 или
или 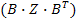 Известно, что из всех операций над матрицами обращение матриц является наиболее трудоемкой, требующей больших затрат времени. Поэтому в настоящее время разработаны более эффективные в общем случае динамического анализа сложных нелинейных схем методы: метод переменных состояния с использованием мал их ( ЭВМ и дифференциально-конечный метод, ориентированный на ЭВМ третьего поколения.
Известно, что из всех операций над матрицами обращение матриц является наиболее трудоемкой, требующей больших затрат времени. Поэтому в настоящее время разработаны более эффективные в общем случае динамического анализа сложных нелинейных схем методы: метод переменных состояния с использованием мал их ( ЭВМ и дифференциально-конечный метод, ориентированный на ЭВМ третьего поколения.
6. Метод сигнальных графов
В основе анализа электрических цепей, изложенного ранее, лежат законы Кирхгофа. Возможен, однако, под- i ход, основанный на причинно-следственных связях между токами и напряжениями в- различных участках схемы, названный методом сигнальных графов.
В отличие от графов рассмотренных ранее, в направленных графах прохождения сигналов (рис. 17 а) каждый узел (вершина) отображает какую-нибудь переменную, а каждая ветвь, соединяющая эти узлы отображает причинно-следственную связь между ними: стрелка на ветви показывает направление передачи: от причины к следствию, а символ соответствующий стрелке, является оператором величины передачи ветви, равной отношению выходной переменной к входной рис.17 б.
Таким образом, одиночная ветвь, связывающая узлы сигнального графа, отображает графически взаимосвязь между переменными, а совокупность узлов и ветвей в виде сигнального графа является топологической моделью системы линейных уравнений и позволяет наглядно представить взаимосвязи различных переменных и коэффициентов этих уравнений. В теории электрических цепей узлами графа обычно являются токи и напряжения- сигналы , отсюда название графа - сигнальный, а ветвями - проводимости, сопротивления или безразмерные величины коэффициентов передач;.
Простейшему уравнению 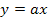 соответствует граф на рис.17 б, имеющий два узла (переменные
соответствует граф на рис.17 б, имеющий два узла (переменные 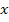 и
и 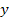 ) и одну ветвь
) и одну ветвь 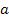 , направленную от причины
, направленную от причины 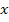 к следствию
к следствию 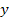 . Узел, отображающий на графе независимую (входную) переменную, называется истоком, а отображающий выходную (зависимую) переменную -стоком. Исток должен содержать только исходящие ветви, а сток -входящие. Прочие узлы называют смешанными. Сигнал передается от одного узла к другому только в направлении стрелки. Поэтому переменная в узле определяется только входящими ветвями, выходящие из узла ветви не оказывают на нее никакого влияния.
. Узел, отображающий на графе независимую (входную) переменную, называется истоком, а отображающий выходную (зависимую) переменную -стоком. Исток должен содержать только исходящие ветви, а сток -входящие. Прочие узлы называют смешанными. Сигнал передается от одного узла к другому только в направлении стрелки. Поэтому переменная в узле определяется только входящими ветвями, выходящие из узла ветви не оказывают на нее никакого влияния.
Теория графов позволяет по определенным правилам провести упрощение сложного графа к более простому виду, из которого можно легко определить передачу графа. Такая процедура эквивалентна алгебраическому решению системы уравнений. Основные правила эквивалентных преобразований поясняющие их примеры приводятся далее,
1. Передача нескольких параллельных, одинаково направленных ветвей равна сумме передач этих ветвей (рис.18а).
2. Передача нескольких последовательных ветвей, соединяющих простые узлы (см. далее), образует путь сигнала, равный произведению передач, входящих в эту последовательность ветвей (рис.18 б). Простым называет узел графа, к которому не подсоединена петля или контур,
3. Исключение петли. Петлей называется ветвь, начинающаяся и кончающаяся в данном узле. Простейшему графу, содержащему петлю (рис.18 в), соответствует уравнение
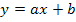 или
или 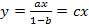
Отсюда очевидно, что исключение петли меняет коэффициент передачи ветвей, которые заканчивались в узле, содержащем петлю 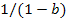 .
.
4. Устранение контура. Контур междукакими-либо узлами имеется направлениями ветвей (рис.18 г).
образуется в графе, когда два пути с противоположными Для передачи от 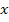 к
к 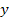 :
:
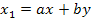
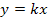
Откуда
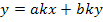
Первый член отображается ветвью с передачей 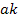 , а второй -петлей с передачей
, а второй -петлей с передачей 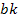 . Для передачи от
. Для передачи от 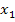 к
к 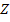 контур
контур 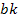 представляет петлю в
представляет петлю в 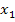 и его устранение равноценно устранению петли по правилу 3.
и его устранение равноценно устранению петли по правилу 3.
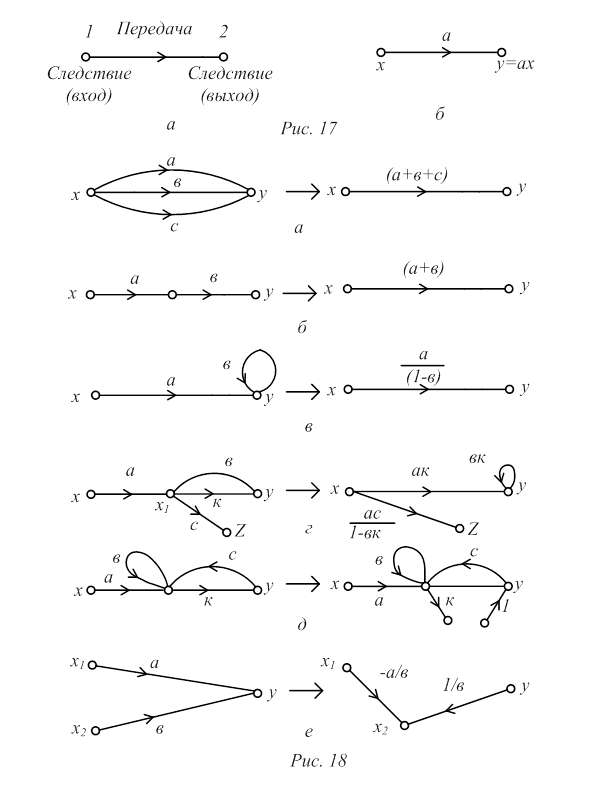
5. Контурная передача 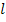 находится после разрыва любой из ветвей контура в любом ее месте. Отношение сигнала, пришедшего к разрыву после обхода контура, к сигналу, посланному в разрыв, называется контурной передачей. Разрывать выбранную ветвь на части надо так, чтобы по одну сторону оставалась ветвь с исходным значением передачи, а по другую - ветвь с единичной передачей, не изменяющая величины передачи вдоль контура. Для рис.18 д, пользуясь правилами 2 и 3, находим значение контурной передачи
находится после разрыва любой из ветвей контура в любом ее месте. Отношение сигнала, пришедшего к разрыву после обхода контура, к сигналу, посланному в разрыв, называется контурной передачей. Разрывать выбранную ветвь на части надо так, чтобы по одну сторону оставалась ветвь с исходным значением передачи, а по другую - ветвь с единичной передачей, не изменяющая величины передачи вдоль контура. Для рис.18 д, пользуясь правилами 2 и 3, находим значение контурной передачи
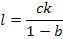
6. Инверсия пути представляет изменение направления какого-либо пути графа на обратное, т.е. замену причины и следствием, что эквивалентно решению уравнений относительно новой переменной. Для графа, приведенного на рис.18 е, уравнение имеет вид
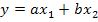
после инверсии
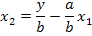
В инвертированном графе ветвь от 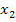 к
к 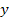 изменяет направление на обратное. Таким образом, при инверсии необходимо изменить направление стрелок всех ветвей, входящих в инвертируемый путь; изменить на обратные (
изменяет направление на обратное. Таким образом, при инверсии необходимо изменить направление стрелок всех ветвей, входящих в инвертируемый путь; изменить на обратные ( 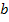 на
на 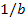 и т.д.) передачи всех ветвей, входящих в инвертируемый путь; концы не инвертируемых ветвей, подходившие к концам ветвей, подлежащих инверсии, после ее выполнения должны находиться там, где теперь находятся концы инвертированных ветвей. Передачи каждой из этих неинвертируемых ветвей делятся на передачу инвертируемой ветви с обратным знаком.
и т.д.) передачи всех ветвей, входящих в инвертируемый путь; концы не инвертируемых ветвей, подходившие к концам ветвей, подлежащих инверсии, после ее выполнения должны находиться там, где теперь находятся концы инвертированных ветвей. Передачи каждой из этих неинвертируемых ветвей делятся на передачу инвертируемой ветви с обратным знаком.
7. Общая формула передачи графа (формула Мэзона) имеет вид
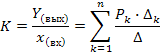
где Рк - передача К -го прямого пути, т.е. пути в котором узлы не встречаются более одного раза от 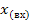 до
до 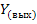
n – число путей; 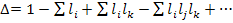 ;
;
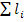 – сумма передач всех контуров и петель ;
– сумма передач всех контуров и петель ;
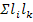 - сумма перемноженных попарно передач всех контуров и петель, не касающихся друг друга, т.е. не имеющих общих узлов;
- сумма перемноженных попарно передач всех контуров и петель, не касающихся друг друга, т.е. не имеющих общих узлов;
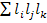 - сумма перемноженных по трое передач всех контуров и петель не касающихся друг друга;
- сумма перемноженных по трое передач всех контуров и петель не касающихся друг друга;
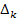 - имеет тот же смысл, что и
- имеет тот же смысл, что и 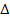 , только относится к передачам контуров и петель, не касающихся К-го пути.
, только относится к передачам контуров и петель, не касающихся К-го пути.
Например, в графе на рис.19 передача от x к y складывается из двух прямых путей

Четырех контырных передач
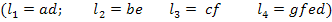
И одной плети
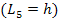
Путь P2 не соприкасается только с 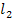 , поэтому
, поэтому 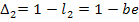 . Для назодления
. Для назодления 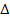 из графа отыскиваем
из графа отыскиваем 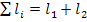 +
+ 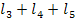 , попарно не касаются дргу друга, в данном графе нет. В результате по формуле Мэзона находим полную передачу графа
, попарно не касаются дргу друга, в данном графе нет. В результате по формуле Мэзона находим полную передачу графа
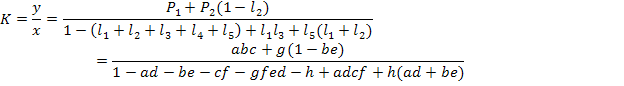
Наибольшее распространение (особенно при анализе электронных схем) получил метод узловых напряжений, приводящий к
значительному сокращению числа уравнений для схем, содержащих общий базовый узел.
Для получения сигнального графа в форме напряжения (или ток) на входе устройства (причина) - напряжение (или ток) на выходе устройства (следствие) обратимся к уравнению . Представим правую часть этого уравнения некоторые эквивалентным током 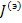 , т.е.
, т.е.
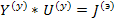
где 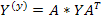 - матрица узловых проводимостей. Рассмотрим структуру матрицы узловых проводимостей. Если обозначить через
- матрица узловых проводимостей. Рассмотрим структуру матрицы узловых проводимостей. Если обозначить через 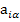 элементы матрицы инциденций
элементы матрицы инциденций 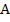 , то элемент транспортированной матрицы
, то элемент транспортированной матрицы 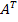 есть
есть 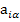 . Элементы матрицы проводимости ветвей
. Элементы матрицы проводимости ветвей 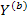 обозначим
обозначим 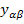 . Поскольку
. Поскольку 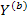 - диагональная матрица, то
- диагональная матрица, то
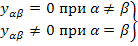
Тогда отдельный элемент матрицы узловых проводимостей согласно правилам произведения матриц выражается так
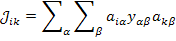
Представим матрицу 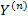 как сумму 2 матриц
как сумму 2 матриц
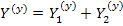
Здесь 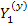 - диагональная матрица с элементами
- диагональная матрица с элементами
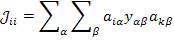
при 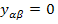 для
для 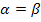 ,
,
Преобразуем матрицу
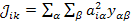 ,
,
откуда следует, что эти элементы не отрицательны, так как 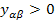 . В то же время
. В то же время 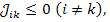 поскольку
поскольку 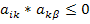 , так как сомножители всегда имеют разные знаки.
, так как сомножители всегда имеют разные знаки.
Используя уравнение, запишем матричное уравнение в виде
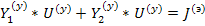
и умножим каждый член его слева на 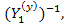 затем выразим узловое напряжение
затем выразим узловое напряжение
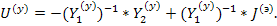
Элементы обратной матрицы 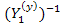 , поскольку она диагональная, равна
, поскольку она диагональная, равна 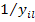 . Тогда, если ввести матрицу
. Тогда, если ввести матрицу 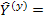
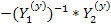 с элементами
с элементами 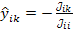 , то уравнение в развернутой форме примет вид:
, то уравнение в развернутой форме примет вид:
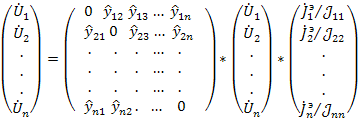
Сигнальный граф, построенный в соответствии с системой уравнений, описываемых матричным уравнением, имеет структуру, показанную на рис.20 б. Передачи ветвей графа могут быть найдены алгебраически по матрицам 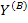 , А. Однако для практической (не машинной) реализации более удобна предлагаемая далее процедура.
, А. Однако для практической (не машинной) реализации более удобна предлагаемая далее процедура.
Для получения сигнального графа по схеме электрических цепей выбирают базовый узел и вводят узловые потенциалы; источники напряжения, содержащиеся в ветвях (кроме входной) преобразуют в источники тока и определяют 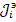 ; пересчитывают все сопротивления в проводимости (в общем случае комплексные или преобразованные по Лапласу); находят проводимости ветвей
; пересчитывают все сопротивления в проводимости (в общем случае комплексные или преобразованные по Лапласу); находят проводимости ветвей 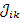 и узловые проводимости
и узловые проводимости 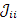 ; определяют передачи ветвей
; определяют передачи ветвей 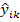 . Узловые проводимости
. Узловые проводимости 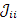 представляют собой проводимость данного узла относительно базового, найденную из условия короткого замыкания всех остальных узлов (т.е. их замыкания на базовый узел). Это условие приводит к следующей формуле для определения собственной узловой проводимости:
представляют собой проводимость данного узла относительно базового, найденную из условия короткого замыкания всех остальных узлов (т.е. их замыкания на базовый узел). Это условие приводит к следующей формуле для определения собственной узловой проводимости:
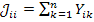 ,
,
где 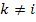 и берутся только те проводимости, которые связывают
и берутся только те проводимости, которые связывают 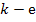 узлы с данным
узлы с данным
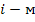 узлом. Взаимные проводимости узлов
узлом. Взаимные проводимости узлов 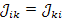 представляют собой фактически проводимости ветвей, соединяющих узлы
представляют собой фактически проводимости ветвей, соединяющих узлы 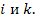 Таким образом,
Таким образом, 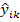 представляет собой взятую с обратным знаком проводимость ветви, соединяющей узел
представляет собой взятую с обратным знаком проводимость ветви, соединяющей узел 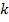 с узлом
с узлом 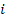 , деленную на собственную проводимость узла
, деленную на собственную проводимость узла 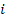 . Учитывая это и формулы
. Учитывая это и формулы
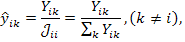
где узловая проводимость 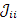 имеет физический смысл весового коэффициента для передачи к данному узлу
имеет физический смысл весового коэффициента для передачи к данному узлу 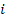 . Аналогично противоположная передача от
. Аналогично противоположная передача от 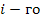 узла к
узла к 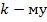 равна
равна
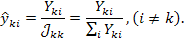
В цепях, не содержащих невзаимных элементов, 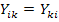 .
.
Далее выбирают на плоскости узлы (кроме базового) с узловыми переменными
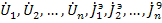 .
.
и соединяют их ветвями с передачей 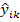 для пар узлов
для пар узлов 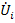 и
и 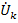 ,
, 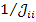 для передачи от узлов
для передачи от узлов 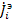 и
и 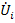 и
и 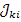 для передач от узлов
для передач от узлов 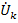 к
к 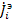 , что приводит к графу, называемому нормализованным сигнальным графом проводимостей. На рис.20 показан пример построения сигнального графа по описанной процедуре. На схеме цепи (рис.20 а) в качестве базового узла взят узел 0. Напряжения узлов 1,2,3,4 относительно узла 0 равны
, что приводит к графу, называемому нормализованным сигнальным графом проводимостей. На рис.20 показан пример построения сигнального графа по описанной процедуре. На схеме цепи (рис.20 а) в качестве базового узла взят узел 0. Напряжения узлов 1,2,3,4 относительно узла 0 равны 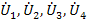 и на ряду с узлом
и на ряду с узлом 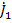 составляют переменные графа (рис.20 б). Собственная узловая проводимость
составляют переменные графа (рис.20 б). Собственная узловая проводимость 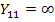 , так как внутреннее сопротивление источника
, так как внутреннее сопротивление источника 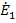 равно 0 и эта передача от узла 2 к узлу 1
равно 0 и эта передача от узла 2 к узлу 1 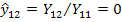 обозначена пунктиром на рис.20 б. Собственная проводимость узла 2 равна
обозначена пунктиром на рис.20 б. Собственная проводимость узла 2 равна 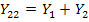 . Способ определения собственных проводимостей проиллюстрирован на примере узла 3 (рис.20 в): закорачивая узлы 2 и 4, получаем
. Способ определения собственных проводимостей проиллюстрирован на примере узла 3 (рис.20 в): закорачивая узлы 2 и 4, получаем 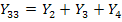 . Аналогично
. Аналогично 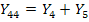 . Взаимные проводимости:
. Взаимные проводимости:
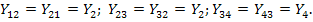
Узел источника тока 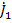 соединяется с узлами
соединяется с узлами 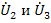 через передачи
через передачи 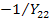 и
и 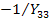 . Деля взаимные передачи, входящие в узлы, на собственные проводимости узлов приходим к структуре графа, показанной на рис.20 б.
. Деля взаимные передачи, входящие в узлы, на собственные проводимости узлов приходим к структуре графа, показанной на рис.20 б.
Необходимо обратить внимание на то, что источник тока отображается на графе ветвями с взаимными передачами 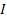 и
и 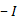 (рис. 20 г), после деления которых на проводимости узлов получаем структуру на рис.20 д, использованную в графе на рис.20 б.
(рис. 20 г), после деления которых на проводимости узлов получаем структуру на рис.20 д, использованную в графе на рис.20 б.
При наличии нескольких ветвей от источника тока в уравнение в качестве 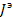 войдет их сумма для тех узлов, с которыми связаны данные источники тока. Если источник тока является входным для некоторого устройства так, что один из его плюсов заземлен (рис. 21 а), то входная часть графа отобразиться одной ветвью с передачей
войдет их сумма для тех узлов, с которыми связаны данные источники тока. Если источник тока является входным для некоторого устройства так, что один из его плюсов заземлен (рис. 21 а), то входная часть графа отобразиться одной ветвью с передачей 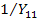 (рис.21 б).
(рис.21 б).
Тензорный метод
Тензорный метод анализа для расчета сложных систем (электрических, механических и др.) был разработан Г.Кроном, который назвал его диакоптикой.
Термин «диакоптика» происходит от греческого слова «копто», озночающего «разрывать» или «разделять на части» и приставки «диа», которая усиливает значение следующего за ней слова. Согласно диакоптике, т.е. методу исследования сложных систем по частям, реальные физические системы можно разделить на части (элементарные или примитивные цепи), рассчитываемые по отдельности, как если бы остальные части системы не существовали. Затем частные решения соединяются шаг за шагом до тех пор, пока не будет получено решение для всей системы.
Рассмотрим некоторую цепь общего вида, в которой действуют источники
напряжения и тока, а между отдельными ветвями существует магнитная связь (взаимоиндукция).
Пусть в ветвях 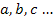 схемы цепи протекают неизвестные токи
схемы цепи протекают неизвестные токи 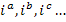 . Выбираем в качестве вспомогательных неизвестных токи хорд (ветвей связи графа данной цепи). Обозначим эти токи, которые могут трактоваться как контурные, через
. Выбираем в качестве вспомогательных неизвестных токи хорд (ветвей связи графа данной цепи). Обозначим эти токи, которые могут трактоваться как контурные, через 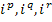 … .
… .
Контурные точки можно рассматривать как координаты вектора 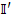 в -мерном пространстве (или, проще, пространстве
в -мерном пространстве (или, проще, пространстве 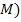 .
.
Токи ветвей можно рассматривать как координаты некоторого другого вектора 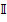 и
и 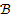 -мерном пространстве (или, проще, пространстве
-мерном пространстве (или, проще, пространстве 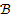 ). Введенные векторы токов выражаются матрицами
). Введенные векторы токов выражаются матрицами
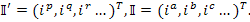
Расположение индексов вверху означает, что эти векторы контрварианты. Токи ветвей всегда можно выразить с помощью I-го закона Кирхгофа или, что одно и то же, приравнять их сумме контурных токов, протекающих в ветвях.
В результате получается следующее выражение:
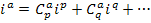
Каждый коэффициент 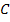 равен 0, +1 или -1 в зависимости от наличия тока в рассматриваемой ветви и от совпадения его направления с принятым для данной ветви за положительное.
равен 0, +1 или -1 в зависимости от наличия тока в рассматриваемой ветви и от совпадения его направления с принятым для данной ветви за положительное.
Таблица коэффициентов 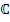 может рассматриваться как матрица преобразования от
может рассматриваться как матрица преобразования от 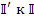 , т.е.
, т.е.
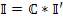
Введенная матрица 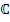 , называемая также матрицей связи или соединений, при соответсвующем выборе дерева графа цепи совпадает с ранее рассмотренной транспортированной матрицей главных контуров, т.е.
, называемая также матрицей связи или соединений, при соответсвующем выборе дерева графа цепи совпадает с ранее рассмотренной транспортированной матрицей главных контуров, т.е.
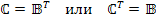 .
.
Для произвольной обобщенной ветви на рис.16 в соответствии с принятыми обозначениями для ветви 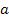 уравнение можно записать в виде
уравнение можно записать в виде
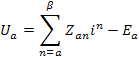
Матрицы, составленные из напряжений и э.д.с. ветвей
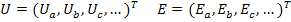 ,
,
представляют собой ковариантные векторы (отмечены нижними индексами). Расходуемая в цепи мощность
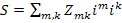 ,
,
откуда следует, что матрица
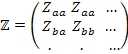
представляет собой дважды ковариантный тензор (тензор полных сопротивлений). Диагональные члены 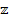 представляют собой собственные полные сопротивления ветвей, а внедиагональные определяются электромагнитной связью ветвей.
представляют собой собственные полные сопротивления ветвей, а внедиагональные определяются электромагнитной связью ветвей.
В обратимых цепях 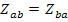 . Например, при взаимоиндукции с коэффициентом
. Например, при взаимоиндукции с коэффициентом 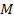 двух ветвях
двух ветвях 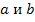
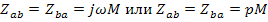
(при решении конкретных задач необходимо придерживаться правил знаков для согласного и встречного включений).
Обобщая соотношение для всех ветвей, запишем
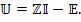
Рассмотрим преобразование, позволяющее перейти от пространства 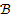 к пространству
к пространству 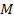 . Оно определенно матрицей связи
. Оно определенно матрицей связи 
| Индексные обозначения | Матричные обозначения | |
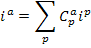 | 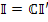 | - определение матрицы связи |
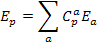 | 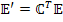 | - ковариантный вектор |
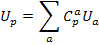 | 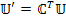 | - ковариантный вектор |
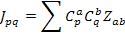 | 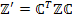 | - дважды ковариантный тензор |
Здесь 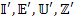 - матрицы, представляющие соответствующие тензорные величины в пространстве
- матрицы, представляющие соответствующие тензорные величины в пространстве 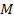 .
.
Соотношение, связывающее тензорные величины, не зависит от выбора системы координат и в пространстве 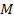 приобретает вид
приобретает вид
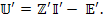
Элементы матрицы 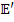 представляют собой алгебраическую сумму э.д.с., действующих в контурах. Элементы главной диагонали
представляют собой алгебраическую сумму э.д.с., действующих в контурах. Элементы главной диагонали 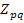 представляют собой собственные сопротивления контуров, а остальные элементы этой матрицы являются сопротивлениями связи между контурами. Каждый элемент матрицы
представляют собой собственные сопротивления контуров, а остальные элементы этой матрицы являются сопротивлениями связи между контурами. Каждый элемент матрицы 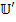 - это сумма разностей потенциалов между зажимами элементов ветвей, встречаемых при последовательном обходе контура. Из 2-го закона Кирхгофа эта сумма равна нулю.
- это сумма разностей потенциалов между зажимами элементов ветвей, встречаемых при последовательном обходе контура. Из 2-го закона Кирхгофа эта сумма равна нулю.
Отсюда
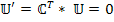
(в ранее приведенных обозначениях это соответствует 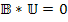 ). Таким образом, соотношение значительно упрощается в пространстве
). Таким образом, соотношение значительно упрощается в пространстве 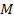 и становиться системой из
и становиться системой из 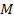 уравнений с
уравнений с 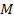 искомыми неизвестными:
искомыми неизвестными:
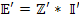 .
.
В основе эквивалентных преобразований электрических цепей в диакоптике лежит постулат инвариантности мощности
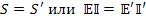 .
.
Последовательность решения задачи методом диакоптики для чистоконтурной цепи (рис.22 а), т.е. цепи, содержащей число контуров равное числу элементарных двухполюсных ветвей, такова.
1. Устанавливают примитивную контурную цепь. Например разделив исходную цепь на 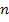 короткозамкнутых частей с токами короткого замыкания, равными токам исходной ветви и приложенными э.д.с. (рис.22 б).
короткозамкнутых частей с токами короткого замыкания, равными токам исходной ветви и приложенными э.д.с. (рис.22 б).
2. Устанавливают тензор полного сопротивления 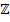 примитивной цепи с числом строк и столбцов, равных числу элементов примитивной цепи.
примитивной цепи с числом строк и столбцов, равных числу элементов примитивной цепи.
3. Записывают вектора 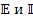 примитивной цепи.
примитивной цепи.
4. Получают матрицу преобразований 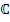 .
.
5. Определяют новые компоненты тензора полного сопротивления 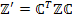
6. Записывают контурные напряжения 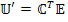 и уравнение напряжения новой цепи
и уравнение напряжения новой цепи 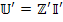 .
.
7. Производят обращение тензора полного сопротивления новой цепи 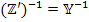
8. Находят неизвестные токи и напряжения 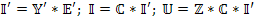 .
.
Разумеется для простых цепей применение диакоптики не оправдано, однако, по мере усложнения цепи и наличия в ней отдельных идентичных элементарных цепей при большом числе электромагнитных связей, затраты умственного и физического труда с применением диакоптики сокращаются пропорционально сложности цепи. Кроме того, применение диакоптики позволяет активно использовать машинные методы расчета.
Теория четырехполюсников
Под четырехполюсниками понимают электрическую цепь или часть цепи (рис.23) с двумя парами зажимов. Пусть входными переменными являются 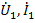 , а выходными
, а выходными 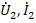 . Любые две из указанных величин можно считать зависимыми и выразить в виде уравнений четырехполюсника через две остальные, принятые за независимые. Число таких уравнений равно шести – числу сочетаний из четырех по два. Коэффициенты уравнений четырехполюсника называют параметрами четырехполюсника.
. Любые две из указанных величин можно считать зависимыми и выразить в виде уравнений четырехполюсника через две остальные, принятые за независимые. Число таких уравнений равно шести – числу сочетаний из четырех по два. Коэффициенты уравнений четырехполюсника называют параметрами четырехполюсника.
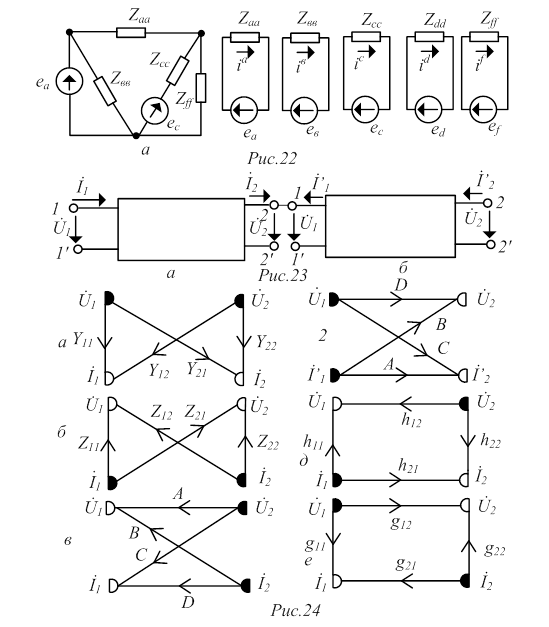
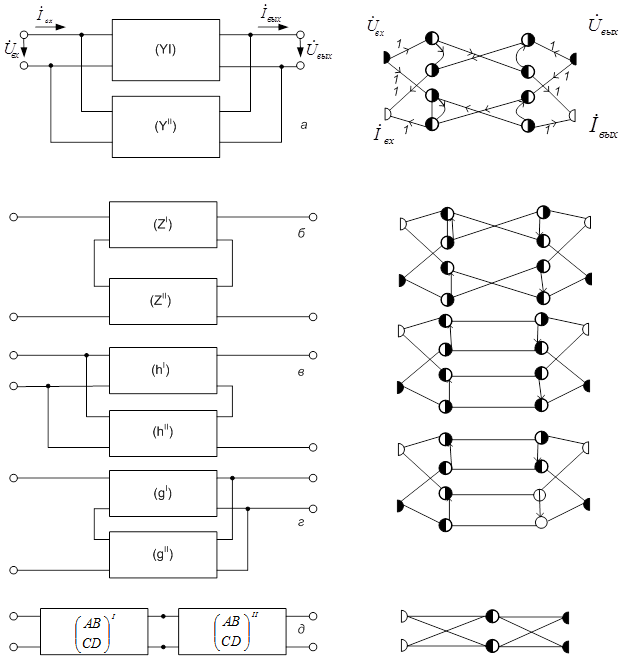
При представлении через параметры проводимостей входное и выходное напряжения ( 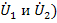 считают аргументами, а токи (
считают аргументами, а токи ( 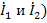 функциями этих аргументов. Взаимосвязь между выбранными переменными можно изобразить в виде сигнального графа (рис.24 а), на котором независимые узлы-источники отмечены условно черными, а зависимые стоки-белыми полукругами. Передачами ветвей служат проводимости. Матричное уравнение, связывающее переменные в соответствии с графом, имеет вид
функциями этих аргументов. Взаимосвязь между выбранными переменными можно изобразить в виде сигнального графа (рис.24 а), на котором независимые узлы-источники отмечены условно черными, а зависимые стоки-белыми полукругами. Передачами ветвей служат проводимости. Матричное уравнение, связывающее переменные в соответствии с графом, имеет вид
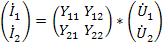
Физический смысл параметров проводимости четырехполюсника определяется из опытов короткого замыкания, а именно: входные проводимости слева и справа при короткозамкнутых противоположных выводах
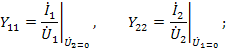
а передаточные проводимости
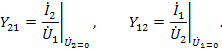
В цепях, соответствующих принципу обратимости, 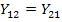 , и, если
, и, если 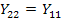 , то четырехполюсник не различим со стороны входных и выходных зажимов и называется симметричным.
, то четырехполюсник не различим со стороны входных и выходных зажимов и называется симметричным.
Если в качестве независимых переменных выбрать токи ( 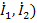 , а зависимых-напряжения (
, а зависимых-напряжения ( 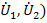 , то взаимосвязь между переменными устанавливается через параметры сопротивлений в виде графа, показанного на рис.24 б и матричного уравнения
, то взаимосвязь между переменными устанавливается через параметры сопротивлений в виде графа, показанного на рис.24 б и матричного уравнения
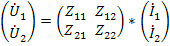
Физический смысл коэффициентов четырехполюсника в данном случае выражается при холостом ходе, а именно: входные сопротивления четырехполюсника слева и справа при разомкнутых противоположных выводах
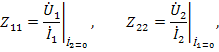
и передаточные сопротивления
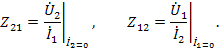
В обратимых цепях 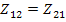 и, если
и, если 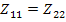 , то четырехполюсник симметричный. Из сравнения формул видно, что матрица параметров сопротивлений (
, то четырехполюсник симметричный. Из сравнения формул видно, что матрица параметров сопротивлений ( 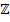 ) является дуальной матрице параметров проводимостей (
) является дуальной матрице параметров проводимостей ( 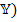 , причем (
, причем ( 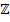 )* (
)* ( 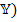 =1.
=1.
Выразим напряжение и ток на входе через напряжение и ток на выходе. Из уравнений получаем:
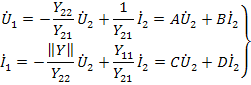
Здесь 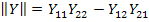 - есть детерминант матрицы проводимостей
- есть детерминант матрицы проводимостей 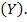
Физический смысл введенных параметров 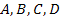 можно установить из рассмотрения режимов холостого хода на выходе
можно установить из рассмотрения режимов холостого хода на выходе
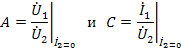
и короткого замыкания на выходе
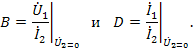
Для линейного пассивного четырехполюсника определитель
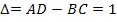 ,
,
а для симметричного 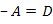 .
.
Сигнальный граф четырехполюсника в форме 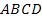 показан на рис. 24 в. Изменяя знаки токов на противоположные (рис.23 б) и решая систему относительно выходных величин, получаем
показан на рис. 24 в. Изменяя знаки токов на противоположные (рис.23 б) и решая систему относительно выходных величин, получаем
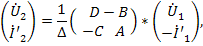
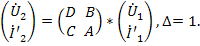
Этой системе соответствует граф, показанный на рис.24 г.
Оставшиеся две системы уравнений выражают через смешанные (гибридные) переменные по размерности и индексу:
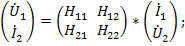
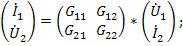
В данных уравнениях выполняются соотношения:
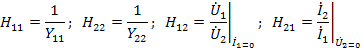
а также
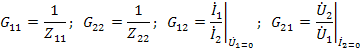
Для обратимых цепей в 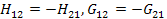 ; в симметричных четырехполюсниках
; в симметричных четырехполюсниках 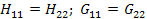 .
.
Каждая система параметров может оказаться более удобной при определенном типе задач. Все рассмотренные параметры связаны друг с другом и могут быть выражены одни через другие.
Для определения параметров четырехполюсников проводят два опыта: холостого хода при
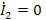 (выходные зажимы разомкнуты) и короткого замыкания при
(выходные зажимы разомкнуты) и короткого замыкания при
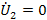 (выходные зажимы закорочены). В опыте холостого хода
(выходные зажимы закорочены). В опыте холостого хода
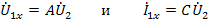 ,
,
откуда 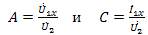
и входное сопротивление со стороны первичных зажимов
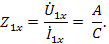
В опыте короткого замыкания
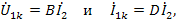
откуда
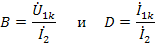
и входное сопротивление со стороны первичных зажимов 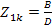
Аналогичные опыты при питании со стороны вторичных зажимов приводят к формулам:
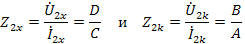
Совместное решение уравнений дает
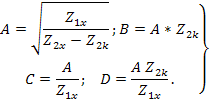
Сопоставляя сигнальные графы, представляющие рассмотренные системы, между собой, можно отметить, что независимые переменные в каждом графе образуют вершине – истоки, а зависимые – стоки.
Соединение четырехполюсников можно отобразить соединением их графов, которое осуществляется либо наложением, либо составлением вершин двух смежных графов. Если некоторая переменная цепи является независимой одновременно для нескольких обьеденяемых четырехполюсников, то вершины – источники отдельных графов должны быть обьеденены (наложены ) в одну общую вершину-источник полного графа. Напротив, если первичная переменная одного четырехполюсника оказывается зависимой для другого, то при соединении их графов вершина – источник и вершина – сток образуют (составлением) внутреннюю вершину, соответствующую этой переменной.
Таким образом, правило соединения графов гласит: «Все налагаемые друг на друга вершины должны быть одного типа, а составленные – различных типов.»
Принципы возможного соединения четырехполюсников и соответствующие им графы показаны на рис. 25. Структуры результирующих графов получаются из соединения соответствующих графов рис. 24 и проилюстрированны на примере параллельного соединения (рис. 25 а): входные и выходные переменные 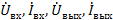 связаны между собой через ветви с единичной передачей и графов четырехполюсников I и II. Из анализа полного графа видно, что он описывается матричным уравнением.
связаны между собой через ветви с единичной передачей и графов четырехполюсников I и II. Из анализа полного графа видно, что он описывается матричным уравнением.
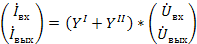
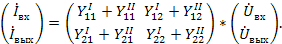
Аналогично суммированием соответствующих матриц находиться результирующие параметры для последовательно-паралельного соединения (рис 25. б) и параллельно-последовательного соединения (рис.25 в). Для каскадного соединения (рис.25 д) результирующая матрица, как это следует из графа, находиться произведением матриц
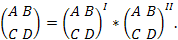
Приведенные правила могут быть распространены на случаи соединения большого числа четырехполюсников. Все указанные виды соединений широко используются в цепях электроники и электроавтоматики, а в последнее время на функциональном уровне проектирования систем.
Введем характеристические параметры четырехполюсника: характеристическое сопротивление и характеристический коэффициент передачи, которые широко используются в теории электрических фильтров.
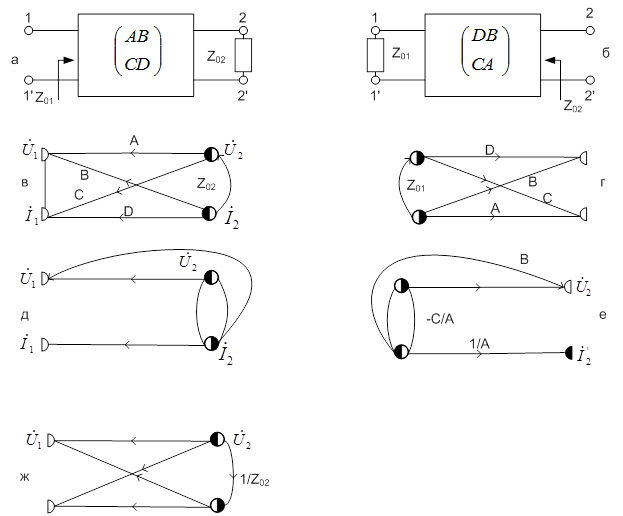
Характеристическим (повторным) сопротивлением симметричного четырехполюсника называют такое сопротивление 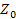 , которое, будучи присоединенным к выходным (входным) зажимам, приводит к тому, что его входное (выходное) сопротивление также будет равно
, которое, будучи присоединенным к выходным (входным) зажимам, приводит к тому, что его входное (выходное) сопротивление также будет равно 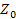 . Для несимметричного четырехполюсника существует два характеристических сопротивления
. Для несимметричного четырехполюсника существует два характеристических сопротивления 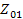 и
и 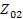 , такие, что при включении
, такие, что при включении 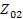 к зажимам 2, 2’ (рис 26. а) характеристическое сопротивление со стороны зажимов 1, 1’ равно
к зажимам 2, 2’ (рис 26. а) характеристическое сопротивление со стороны зажимов 1, 1’ равно 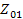 и наоборот, при включении к зажимам 1, 1’ (рис.26 б) сопротивления
и наоборот, при включении к зажимам 1, 1’ (рис.26 б) сопротивления 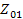 , сопротивление на зажимах 2, 2’ равно
, сопротивление на зажимах 2, 2’ равно 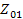 .
.
По определению:
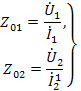
Рассмотрим сигнальный граф прямой и обратной передач четырехполюсника, когда он нагружен на соответствующее характеристическое сопротивление (рис.26 в,г). Для определения 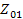 из графа на рис.26 в по формуле и необходимо найти передачу от
из графа на рис.26 в по формуле и необходимо найти передачу от 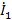 к
к 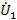 , при етом узел
, при етом узел 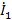 , должен быть истоком, а ветвь
, должен быть истоком, а ветвь 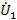 – стоком. Узел
– стоком. Узел 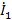 можно превратить в исток, инвертируя ветвь D, т.е. направив ее в
можно превратить в исток, инвертируя ветвь D, т.е. направив ее в 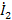 . После инверсии ее передача станет равной 1/D, кроме того, ветвь С, входящая в этот узел, теперь должна быть направлена также в узел
. После инверсии ее передача станет равной 1/D, кроме того, ветвь С, входящая в этот узел, теперь должна быть направлена также в узел 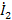 , а ее передача будет равно –C/D (рис.26 д)
, а ее передача будет равно –C/D (рис.26 д)
По формуле Мэзона из графа, показанного на рис.26 д, получим
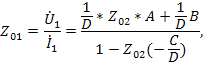
откуда 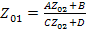
Аналогично, преобразуя граф обратной передачи (рис.26 г), получаем граф, показанный на рис. 26 е, из которого
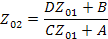
Решая систему из двух последних уравнений, получаем
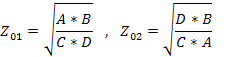
Используя взаимосвязь параметров четырехполюсника, можно выразить характеристические сопротивления через параметры холостого хода и короткого замыкания, откуда
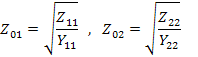
Для симметричного четырехполюсника 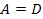 ,
, 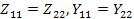 так, что
так, что
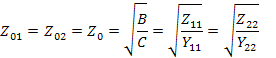
Из уравнений найдем
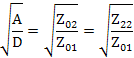
Характеристические сопротивления не описывают полностью поведение четырехполюсника, так как каждое из них относиться лишь к одной паре зажимов. Вторым основным характеристическим параметром является характеристическая передача. Вычислим коэффициенты передач четырехполюсника по току и напряжению. Из графа на рис. 26 находим