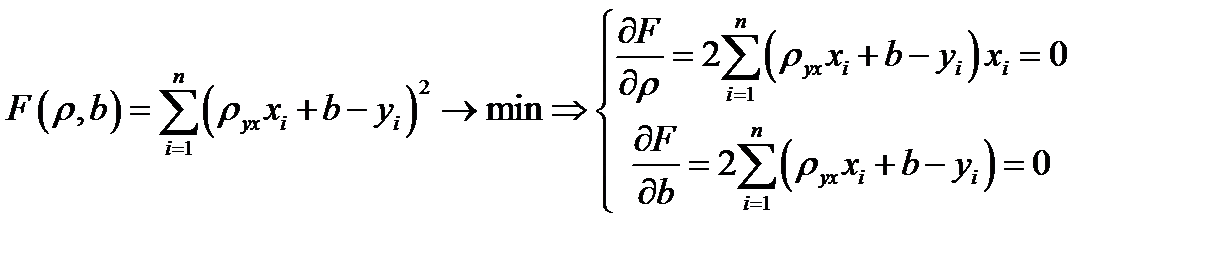Генеральная и выборочная совокупность.
Оп. 1.В математической статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном наборе условий. Понятие генеральной совокупности, в определенном смысле, аналогично понятию случайной величины.
Оп. 2.Часть наблюдаемых значений с. в., на основании которых делают вывод о ее свойствах, называется выборкой.Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (выборке) выносится суждение о ее свойствах в целом.
Оп. 3.Выборка называется репрезентативной (представительной), если она достаточно хорошо воспроизводит генеральную совокупность.
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. Случайность отбора элементов в выборку достигается соблюдением принципа равной возможности всем элементам генеральной совокупности быть отобранными в выборку.
Математическая теория выборочного метода основывается на анализе собственно-случайной выборки, образованной случайным выбором элементов по одному без расчленения генеральной совокупности на части или группы.
Используют два способа образования выборки:
• повторный отбор (по схеме возвращенного шара), когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран;
• бесповторный отбор (по схеме невозвращенного шара), когда отобранный элемент не возвращается в общую совокупность.
Вариационные ряды, их характеристики и графическое изображение.
Оп. 4.Различные значения с. в. 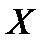 (признака) в выборке называются вариантами (обозначаем их через
(признака) в выборке называются вариантами (обозначаем их через  ). В случае
). В случае  испытаний с. в.
испытаний с. в. 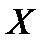 символически запишем ряд значений:
символически запишем ряд значений: 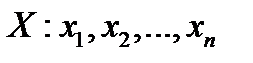 .
.
Оп. 5.Расположение вариантов в порядке возрастания (убывания) называется ранжированием ряда:  .
.
Оп. 6.Разбивка ранжированного ряда значений с. в. 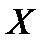 на частичные интервалы называется группировкой.
на частичные интервалы называется группировкой.
Согласно формуле Стерджеса, рекомендуемое число интервалов 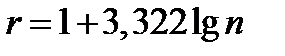 , а длина частичного интервала (шаг)
, а длина частичного интервала (шаг) 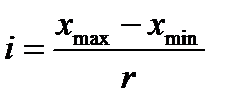 .
.
Оп. 7.Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами  , а отношение их к общему числу наблюдений — частостями или относительными частотами
, а отношение их к общему числу наблюдений — частостями или относительными частотами 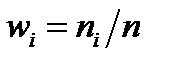 . Частоты и частости называются весами.
. Частоты и частости называются весами.
Оп. 8. Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами. Различают дискретные и непрерывные вариационные ряды. Варианты дискретного ряда являются значениями ДСВ, а непрерывного – НСВ.
Дискретный вариационный ряд, с относительными частотами в качестве весов, служит оценкой закона распределения ДСВ по данным выборки.
Оп. 9. Накопленная частота 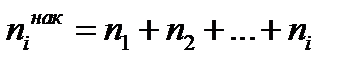 показывает, сколько наблюдалось вариантов со значением признака, меньшим
показывает, сколько наблюдалось вариантов со значением признака, меньшим  . Отношение накопленной частоты
. Отношение накопленной частоты 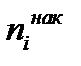 к общему числу наблюдений
к общему числу наблюдений 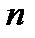 назовем накопленной частостью
назовем накопленной частостью 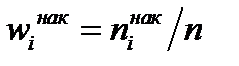 .
.
Оп. 10. Полигон – ломаная линия, в которой концы отрезков прямой имеют координаты 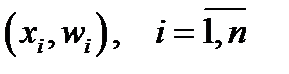 .
.
Полигон служит для графического изображения вариационного ряда ДСВ. По теореме Бернулли относительные частоты оценивают по статистическим данным вероятности того, что ДСВ Х в результате испытания примет значение 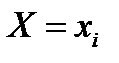 . Т. о. полигон дает графическую оценку закона распределения ДСВ по данным выборки.
. Т. о. полигон дает графическую оценку закона распределения ДСВ по данным выборки.
Оп. 11. Гистограмма - ступенчатая фигура из прямоугольников с основаниями, равными длинам интервалов  и высотами равными плотностям частостей
и высотами равными плотностям частостей 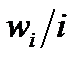 интервалов.
интервалов.
Гистограмма служит для графического изображения вариационных рядов НСВ. По теореме Бернулли, плотность относительной частоты может служить оценкой плотности распределения вероятности НСВ Х по данным выборки, а относительная частота 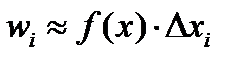 служит оценкой вероятности того, что значение Х попадет внутрь интервала
служит оценкой вероятности того, что значение Х попадет внутрь интервала  . Площадь гистограммы равна единице – таким свойством обладает кривая плотности распределения НСВ. Т. о. гистограмма служит графической оценкой плотности распределения вероятностей НСВ по выборочным данным.
. Площадь гистограммы равна единице – таким свойством обладает кривая плотности распределения НСВ. Т. о. гистограмма служит графической оценкой плотности распределения вероятностей НСВ по выборочным данным.
Оп. 12. Кумулятивная кривая(кумулята) – кривая накопленных частостей. Для дискретного ряда – ломанная линия  . Для интервального ряда ломанная линия начинается в точке
. Для интервального ряда ломанная линия начинается в точке 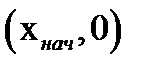 , а другие ее точки соответствуют концам интервалов.
, а другие ее точки соответствуют концам интервалов.
Накопленные частости  оценивают по выборочным данным вероятности
оценивают по выборочным данным вероятности  . Кумулята служит графической оценкой интегральной функции распределения
. Кумулята служит графической оценкой интегральной функции распределения 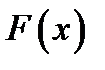 по выборочным данным.
по выборочным данным.
Пример 1. Получены данные по показателям суточного водопотребления жилого массива города, 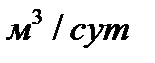 :
:
174 166 174 146 173 165 188 161 150 158
173 164 150 156 142 171 154 175 189 140
157 164 168 171 170 158 186 165 185 172
168 170 163 176 160 172 163 162 178 155
180 162 156 148 160 156 148 150 167 166
154 166 165 181 177 152 145 167 177 185
Провести графическую оценку плотности распределения и интегральной функции НСВ суточного водопотребления по данным выборки.
Составим вариационный ряд.

| Интервалы | Частоты  | Частости  | Плотность частости 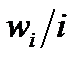 | Накопленные частости  |
 | 0.067 | 0.0095 | 0.067 | |
 | 0.133 | 0.019 | 0.2 | |
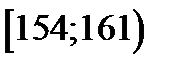 | 0.167 | 0.024 | 0.367 | |
 | 0.267 | 0.038 | 0.633 | |
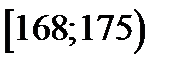 | 0.183 | 0.026 | 0.817 | |
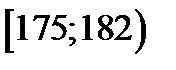 | 0.1 | 0.014 | 0.917 | |
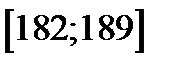 | 0.083 | 0.012 | ||
 | 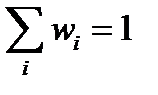 |
По данным таблицы составим гистограмму плотностей частостей (рис. 1) и кумулятивную кривую (рис. 2).
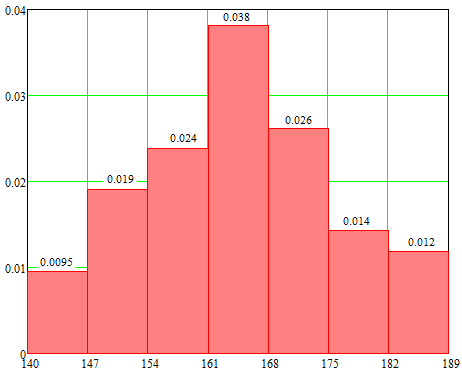

Рис. 1. Гистограмма Рис. 2. Кумулята.
Лекция №3. Точечные и интервальные оценки параметров генеральной совокупности.
Характеристики генеральной и выборочной совокупности.
Средняя арифметическая и ее свойства. Медиана, мода, показатели вариации. Дисперсия, ее свойства. Моменты вариационного ряда. Показатели асимметрии.
Доверительные интервалы. Необходимая численность выборки.
Точечные характеристики генеральной и выборочной совокупности.
Оп. 1.Числа объектов (наблюдений) в генеральной  или выборочной
или выборочной  совокупности называются их объемами.
совокупности называются их объемами.
Генеральная совокупность может иметь как конечный, так и бесконечный объем.
Пусть  и
и  соответственно число элементов генеральной и выборочной совокупностей, обладающих значением признака
соответственно число элементов генеральной и выборочной совокупностей, обладающих значением признака 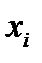 . Тогда можно рассмотреть основные точечные характеристики:
. Тогда можно рассмотреть основные точечные характеристики:
| Характеристика | Генеральная совокупность | Выборка |
| Средняя |  | 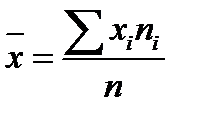 |
| Дисперсия | 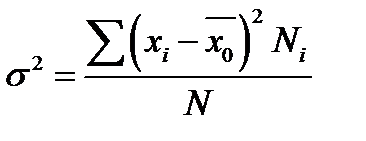 | 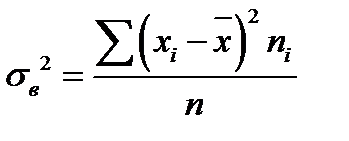 |
| Доля (относительная частота) |  | 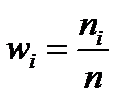 |
Замечание 1. В случае бесконечной генеральной совокупности 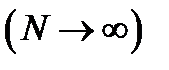 , в соответствии с теоремой Бернулли, под генеральными средней и дисперсией понимается соответственно математическое ожидание
, в соответствии с теоремой Бернулли, под генеральными средней и дисперсией понимается соответственно математическое ожидание  и дисперсия
и дисперсия 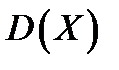 распределения признака X, а под генеральной долей
распределения признака X, а под генеральной долей 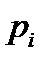 — вероятность данного события.
— вероятность данного события.
Оп. 2.Оценкой  параметра
параметра  называют всякую функцию результатов наблюдений над случайной величиной X, с помощью которой судят о значении параметра
называют всякую функцию результатов наблюдений над случайной величиной X, с помощью которой судят о значении параметра  :
: 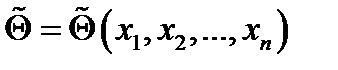 .
.
Замечание 2. Так как 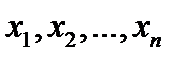 - значения с. в. Х и могут изменяться от выборки к выборке, то
- значения с. в. Х и могут изменяться от выборки к выборке, то  - сама по себе является случайной величиной,в отличие от оцениваемого параметра
- сама по себе является случайной величиной,в отличие от оцениваемого параметра  . Поэтому, о качестве оценки следует судить не по индивидуальным ее значениям, а лишь по распределению ее значений в большой серии испытаний.
. Поэтому, о качестве оценки следует судить не по индивидуальным ее значениям, а лишь по распределению ее значений в большой серии испытаний.
В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.
Оп. 3.Оценка  параметра
параметра  называется несмещенной, если ее математическое ожидание равно оцениваемому параметру:
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: 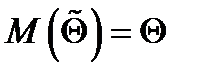 .
.
Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оп. 4.Оценка  параметра
параметра  называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру: 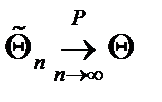 .
.
В случае использования состоятельных оценок, при достаточно больших объемах выборки, становятся маловероятными значительные ошибки при оценивании.
Оп. 5.Несмещенная оценка  параметра
параметра  называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок, вычисленных по выборкам одного и того же объема
называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок, вычисленных по выборкам одного и того же объема  .
.
Если рассматривать в качестве оценок генеральной средней и доли соответствующие точечные характеристики выборки, то из теорем Чебышева и Бернулли сразу следует их состоятельность.
Для того, чтобы смоделировать получение выборки значений с. в. Х объема  , рассмотрим
, рассмотрим  одинаковых с. в.
одинаковых с. в.  с равными математическими ожиданиями. Тогда:
с равными математическими ожиданиями. Тогда:
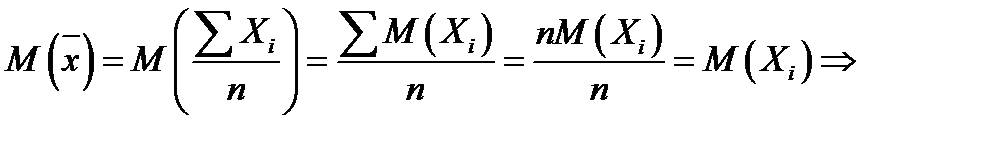 оценка генеральной средней в виде выборочной средней является несмещенной. Для повторной выборки
оценка генеральной средней в виде выборочной средней является несмещенной. Для повторной выборки  - оценка эффективная.
- оценка эффективная.
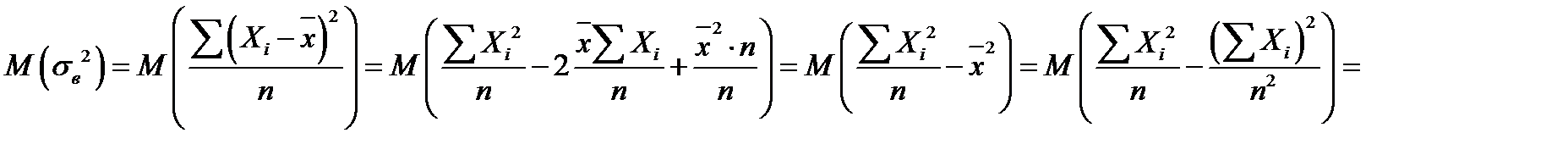
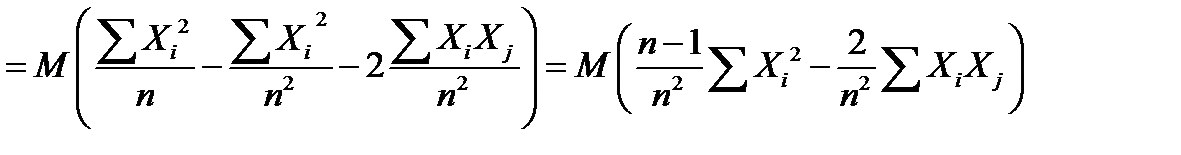 .
.
Выборочная дисперсия, как мера разброса, не зависит от расположения координатных осей. Перенесем начало СК в точку с координатой 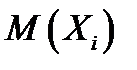 . Тогда новые значения случайных величин
. Тогда новые значения случайных величин 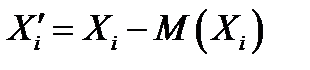 . Выражение для
. Выражение для 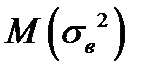 в новой СК можно записать:
в новой СК можно записать:

Последнее равенство справедливо для случая повторнойвыборки, так как при этом с. в. 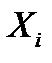 и
и  являются взаимно-независимыми. Из последнего равенства следует, что
являются взаимно-независимыми. Из последнего равенства следует, что 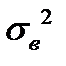 является смещенной оценкой дисперсии генеральной совокупности. В качестве несмещенной оценки дисперсии используется величина
является смещенной оценкой дисперсии генеральной совокупности. В качестве несмещенной оценки дисперсии используется величина 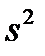 :
:
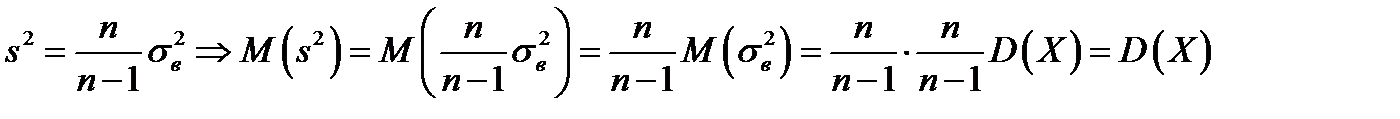
Замечание 3. Аналогичный результат для оценки дисперсии можно получить и для бесповторной выборки.
Замечание 4. При достаточно большом объеме выборки 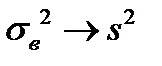 .
.
Рассмотрим вопрос о несмещенности оценки доли генеральной совокупности. Для случая повторной выборки рассмотрим  одинаковых с. в.
одинаковых с. в.  каждая из которых – с. в. числа проявления интересующего значения в
каждая из которых – с. в. числа проявления интересующего значения в  -м испытании. С. в.
-м испытании. С. в.  может принимать значения
может принимать значения  и распределена по закону Бернулли. В теории вероятностей показано, что
и распределена по закону Бернулли. В теории вероятностей показано, что 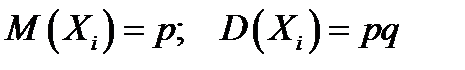 , где
, где 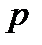 - вероятность проявления значения интересующего значения в однократном испытании.
- вероятность проявления значения интересующего значения в однократном испытании.
 - оценка несмещенная.
- оценка несмещенная.
Замечание 5. Полученные выводы применимы и для бесповторной выборки, если ее объем значительно меньше объема генеральной совокупности. Это положение часто используется на практике.
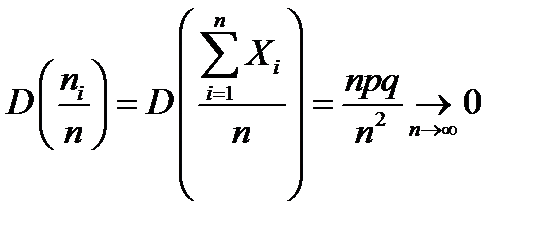 - оценка эффективная.
- оценка эффективная.
Т. о. для оценки значения средней генеральной совокупности по данным выборки используется выборочная средняя:
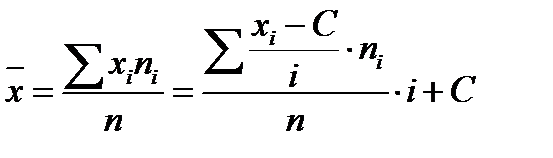 ,
,
где С –варианта с набольшей частотой, 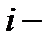 шаг интервала.
шаг интервала.
Для оценки дисперсии генеральной совокупности используется исправленная выборочная дисперсия:
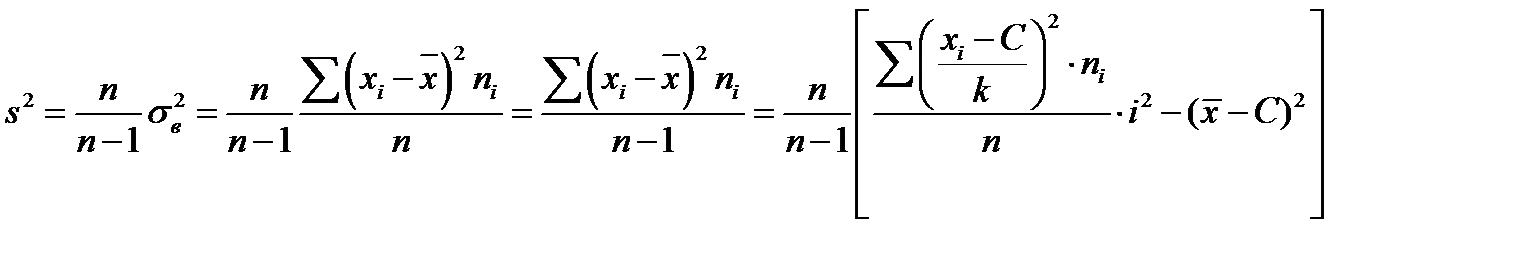
При анализе интервального ряда в качестве вариант рассматриваются середины интервалов.
Пример 2. По данным примера 1 определить выборочную среднюю и дисперсию, коэффициент вариации, медиану и моду распределения с. в. водопотребления.
| Середины | Частоты | 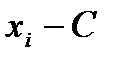 С=164,5 С=164,5 | 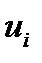 | 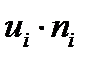 | 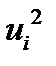 |  |
| 143,5 | -21 | -3 | -12 | |||
| 150,5 | -14 | -2 | -16 | |||
| 157,5 | -7 | -1 | -10 | |||
| 164,5 | ||||||
| 171,5 | ||||||
| 178,5 | ||||||
| 185,5 | ||||||
 | - | - | - |
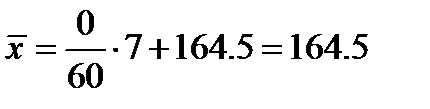 ;
; 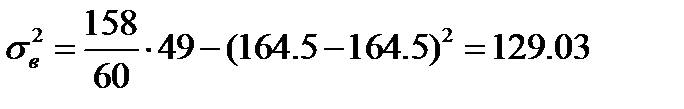 ;
; 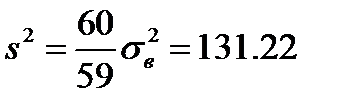 .
.
Определим коэффициент вариации выборки: 
Вводя обозначения 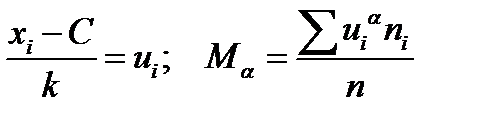 , запишем формулы для оценки величины асимметрии
, запишем формулы для оценки величины асимметрии 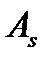 и эксцесса
и эксцесса 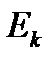 :
:

| Середины | Частоты |  |  | 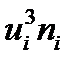 | 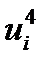 | 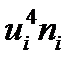 |
| 143,5 | -3 | -27 | -108 | |||
| 150,5 | -2 | -8 | -64 | |||
| 157,5 | -1 | -1 | -10 | |||
| 164,5 | ||||||
| 171,5 | ||||||
| 178,5 | ||||||
| 185,5 | ||||||
 | - | - | - |
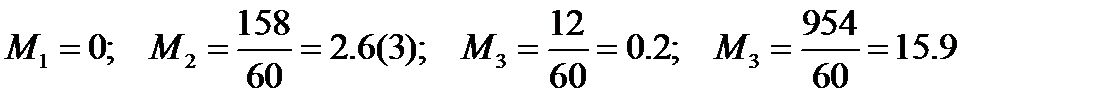
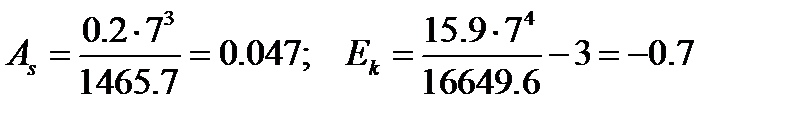
Определение моды и медианы можно, в первом приближении, провести графическими методами. Графически получим:

Для вычисления моды 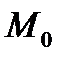 и медианы
и медианы 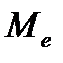 из интервальных рядов прибегают к интерполяционным формулам:
из интервальных рядов прибегают к интерполяционным формулам:

 ,
, 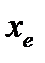 - нижние границы модального и медианного интервалов соответственно;
- нижние границы модального и медианного интервалов соответственно; 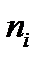 ,
,  и
и 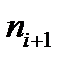 - частоты модальных (медианных), пред- и после модальных (медианных) интервалов соответственно. Выписанные формулы являются аналитическим выражением для х координаты точки пересечения прямых на рисунке, т. е. являются линейной интерполяцией изменения частот (накопленных частот) на модальном (медианном) интервале.
- частоты модальных (медианных), пред- и после модальных (медианных) интервалов соответственно. Выписанные формулы являются аналитическим выражением для х координаты точки пересечения прямых на рисунке, т. е. являются линейной интерполяцией изменения частот (накопленных частот) на модальном (медианном) интервале.
Модальный интервал находят как интервал, на котором гистограмма, являющаяся оценкой кривой плотности распределения по данным выборки, принимает максимальное значение. Т. е. модальный интервал соответствует интервалу с наибольшей плотностью относительной частоты.
Медианный интервал должен содержать оценку квантиля 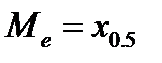 . Т. е. в этом интервале относительная накопленная частота должна достичь значения
. Т. е. в этом интервале относительная накопленная частота должна достичь значения 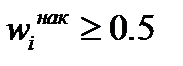 .
.
По данным расчетной таблицы предшествующей лекции модальный и медианный интервалы совпадают:
 ;
; 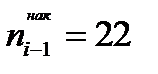 ;
;  ;
;  ;
; 
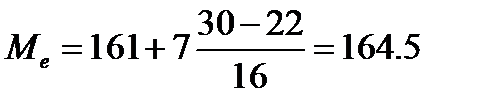
По данным вычислений 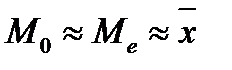 .
.
Интервальные оценки.
Точечная оценка  параметра
параметра  является некоторым приближением к истинному значению. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку.
является некоторым приближением к истинному значению. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку.
Оп. 6. Интервальной оценкойпараметра  называют числовой интервал
называют числовой интервал  , который с заданной вероятностью
, который с заданной вероятностью 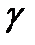 накрывает неизвестное значение параметра
накрывает неизвестное значение параметра  .
.
Числа 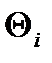 находятся по выборочным данным и являются случайными величинами. Величина доверительного интервала уменьшается при
находятся по выборочным данным и являются случайными величинами. Величина доверительного интервала уменьшается при 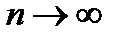 и возрастает при
и возрастает при 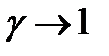 .
.
Доверительный интервал для генеральной средней.
В случае повторной выборки  , где
, где 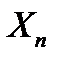 - независимые, одинаково распределенные с. в. с конечными математическими ожиданиями и дисперсиями. Следовательно, по теореме Ляпунова, при
- независимые, одинаково распределенные с. в. с конечными математическими ожиданиями и дисперсиями. Следовательно, по теореме Ляпунова, при  распределение
распределение 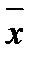 приближается к нормальному
приближается к нормальному  . Для бесповторной выборки
. Для бесповторной выборки 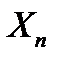 - зависимые с. в. Но и в этом случае можно показать, что закон распределение как угодно близок к нормальному.
- зависимые с. в. Но и в этом случае можно показать, что закон распределение как угодно близок к нормальному.
1. Случай больших выборок.
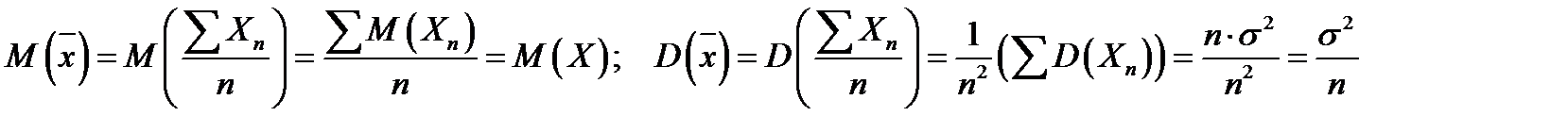

В последнем выражении  - среднее квадратичное отклонение генеральной совокупности. Если
- среднее квадратичное отклонение генеральной совокупности. Если  неизвестно, то по законам больших чисел, при больших объемах выборки ее можно заменить оценкой
неизвестно, то по законам больших чисел, при больших объемах выборки ее можно заменить оценкой 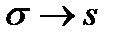 .
.
Из последнего равенства найдем  . Выбирая
. Выбирая  достаточно близким к единице, можно считать, что с заданной степенью надежности неравенство
достаточно близким к единице, можно считать, что с заданной степенью надежности неравенство 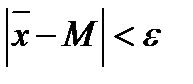 выполняются. Откуда следует, что:
выполняются. Откуда следует, что:

Дисперсия 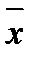 была найдена для случая повторной выборки
была найдена для случая повторной выборки  . Для бесповторной выборки показано, что
. Для бесповторной выборки показано, что 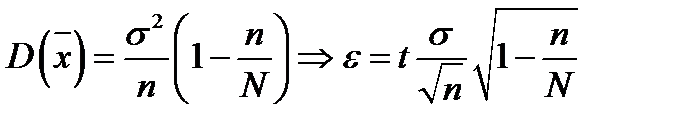 . Из полученных формул следует, что необходимый объем повторной выборки для получения оценки математического ожидания с надежностью
. Из полученных формул следует, что необходимый объем повторной выборки для получения оценки математического ожидания с надежностью 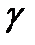 и ошибкой, не превышающей
и ошибкой, не превышающей  :
:

Для бесповторной выборки аналогичная формула выглядит  .
.
2. Случай малых выборок.
Задача построения доверительного интервала для генеральной средней может быть решена, если признак генеральной совокупности имеет нормальное распределение. Тогда распределение  также будет нормальным для любого числа слагаемых.
также будет нормальным для любого числа слагаемых.
Случайная величина 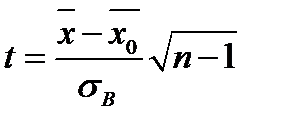 распределена по закону Стьюдента.
распределена по закону Стьюдента.  -распределение симметрично относительно оси ординат, но более пологое по сравнению с нормальным. При
-распределение симметрично относительно оси ординат, но более пологое по сравнению с нормальным. При 
 -распределение неограниченно приближается к нормальному. При
-распределение неограниченно приближается к нормальному. При 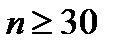 можно считать распределение нормальным.
можно считать распределение нормальным.
Плотность распределения  является функцией только объема выборки. В соответствии со свойствами непрерывных случайных величин, величина вероятности
является функцией только объема выборки. В соответствии со свойствами непрерывных случайных величин, величина вероятности
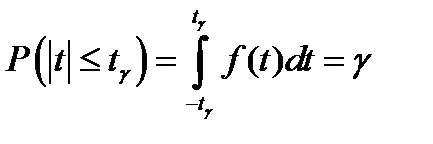
Вычисляя значение интеграла при различных  составляют таблицы
составляют таблицы 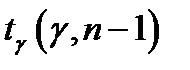 .Интервальная оценка генеральной средней:
.Интервальная оценка генеральной средней:
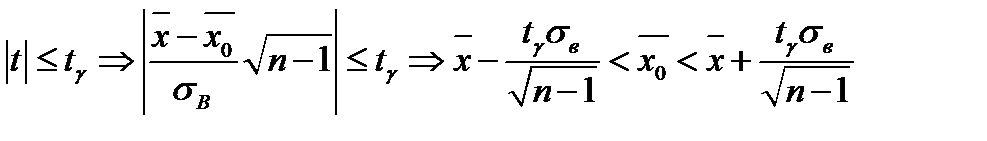
Величина 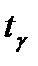 находится из статистических таблиц
находится из статистических таблиц  .
.
Доверительный интервал для генеральной доли.
1. Случай больших выборок.
Несмещенной и эффективной оценкой генеральной доли  служит относительная частота выборочной совокупности
служит относительная частота выборочной совокупности 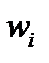 . С. в.
. С. в. 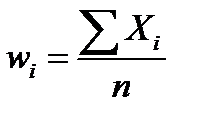 , где
, где  - с. в. числа проявлений события A в i-м испытании. Каждая с. в.
- с. в. числа проявлений события A в i-м испытании. Каждая с. в.  распределена по биномиальному закону. Но если выборка повторная (
распределена по биномиальному закону. Но если выборка повторная (  - взаимно независимы), то сумма их достаточно большого количества распределена нормально (ЦПТ теорема Ляпунова). Ранее показано, что
- взаимно независимы), то сумма их достаточно большого количества распределена нормально (ЦПТ теорема Ляпунова). Ранее показано, что  . Тогда, по аналогии с интервальной оценкой математического ожидания:
. Тогда, по аналогии с интервальной оценкой математического ожидания:
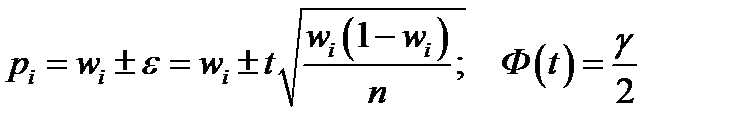
Необходимый объем выборки  . В случае бесповторной выборки максимальная ошибка
. В случае бесповторной выборки максимальная ошибка  .
.
2. Случай умеренно больших выборок.
Объем выборки не настолько велик, чтобы вместо доли генеральной совокупности использовать относительную частоту выборки, но распределение с. в. 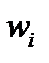 можно считать близким к нормальному. Тогда
можно считать близким к нормальному. Тогда 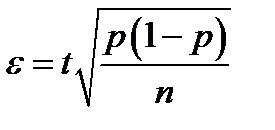 , и для нахождения интервальной оценки необходимо решить неравенство:
, и для нахождения интервальной оценки необходимо решить неравенство:

Пример 3. По данным предыдущих задач составить интервальные оценки генеральной средней и генеральной доли суточного водопотребления объемом 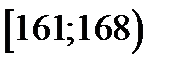
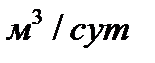 при доверительной вероятности
при доверительной вероятности  .
.


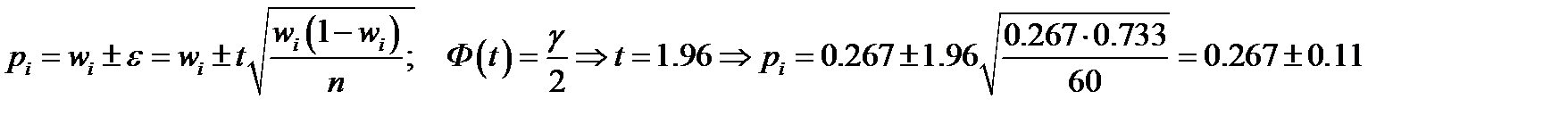
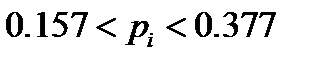
Лекция №4. Статистические гипотезы.
Проверка статистических гипотез. Критерий Пирсона.
Оп. 1. Статистическойназывают гипотезу о виде неизвестного закона распределения или о параметрах известных законов распределений.
Выдвинутую гипотезу называют нулевой  . Наряду с нулевой гипотезой рассматривают и альтернативную (противоположную) ей гипотезу
. Наряду с нулевой гипотезой рассматривают и альтернативную (противоположную) ей гипотезу  . Если в процессе анализа ситуации нулевая гипотеза отвергается, то автоматически принимается альтернативная гипотеза.
. Если в процессе анализа ситуации нулевая гипотеза отвергается, то автоматически принимается альтернативная гипотеза.
Нулевая гипотеза может быть, как правильной, так и нет. Возникает необходимость ее проверки. Проверку проводят статистическими методами, следовательно, есть некоторая вероятность того, что будет принято неправильное решение. Могут быть допущены ошибки:
1. Ошибка первого рода – отвергнута правильная гипотеза. Вероятность этой ошибки обозначим 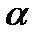 , ее называют уровнем значимости.
, ее называют уровнем значимости.
2. Ошибка второго рода – принята неправильная гипотеза. Вероятность этой ошибки обозначим 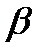 .
.
Оп. 2. Статистическим критерием называют случайную величину 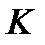 , точное или приближенное распределение которой известно, служащую для проверки нулевой гипотезы.
, точное или приближенное распределение которой известно, служащую для проверки нулевой гипотезы.
Оп. 3. Наблюдаемым значением  называют значение критерия, вычисленное по данным выборки, в предположении справедливости гипотезы
называют значение критерия, вычисленное по данным выборки, в предположении справедливости гипотезы 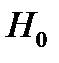 .
.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая—при которых она принимается.
Оп. 4. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области—гипотезу 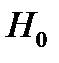 отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы - гипотезу
отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы - гипотезу 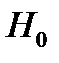 принимают.
принимают.
Оп. 5. Критическими точками 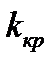 называют точки, отделяющие критическую область от области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
называют точки, отделяющие критическую область от области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Оп. 6. Правосторонней называют критическую область, определяемую как 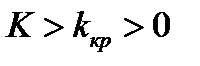 . Левосторонней называют критическую область
. Левосторонней называют критическую область 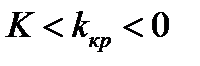 . Двусторонней называют критическую область, определяемую неравенствами
. Двусторонней называют критическую область, определяемую неравенствами  .
.
Замечание 1. Наблюдаемое значение критерия может оказаться выходящим за границы области принятия гипотезы не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки
равна уровню значимости  .
.
Замечание 2. Пусть нулевая гипотеза принята; ошибочно думать, что тем самым она доказана. Действительно, известно, что один пример, подтверждающий справедливость некоторого общего утверждения, еще не доказывает его. Поэтому – более правильно говорить «данные наблюдений согласуются с кулевой гипотезой и, следовательно, не дают оснований ее отвергнуть».
На практике для большей уверенности принятия гипотезы ее проверяют другими способами или повторяют эксперимент, увеличив объем выборки.
Отвергают гипотезу более категорично, чем принимают. Действительно, известно, что достаточно привести один пример, противоречащий некоторому общему утверждению, чтобы это утверждение отвергнуть. Если оказалось, что наблюдаемое значение критерия принадлежит критической области, то этот факт и служит примером, противоречащим нулевой гипотезе, что позволяет ее отклонить.
Процедуру проверки статистической гипотезы поясним на примере проверки гипотезы о значении параметра распределения.
Пример 4. Сухую строительную смесь упаковывают в пакеты с номинальным весом 1 кг. Упаковочная машина работает со средним квадратичным отклонением 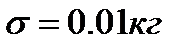 . Случайная выборка объемом
. Случайная выборка объемом  пакетов готовой продукции выявила средний вес
пакетов готовой продукции выявила средний вес  . Имеется ли какое-либо основание предполагать, что фасовочная машина работает без нарушений в настройке?
. Имеется ли какое-либо основание предполагать, что фасовочная машина работает без нарушений в настройке?
Если фасовочная машина работает без нарушений в настройке, то ошибки в заявленном весе пакета носят случайный характер и математическое ожидание с. в. 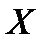 - веса отдельно взятого пакета будет равно 1 кг.
- веса отдельно взятого пакета будет равно 1 кг.
В качестве нулевой гипотезы, выдвинем предположение -  , а альтернативную гипотезу сформулируем как
, а альтернативную гипотезу сформулируем как 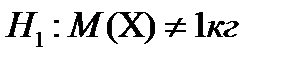 . Предположим, что с. в.
. Предположим, что с. в. 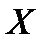 распределена по нормальному закону, тогда распределение ее выборочной средней
распределена по нормальному закону, тогда распределение ее выборочной средней 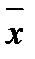 также будет нормальным.
также будет нормальным.
В качестве статистического критерия выберем с. в. 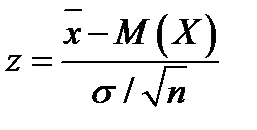 , которая при вышеназванных условиях имеет нормальное распределение. Найдем число
, которая при вышеназванных условиях имеет нормальное распределение. Найдем число 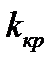 , для которого справедливо равенство:
, для которого справедливо равенство:

Таким образом, с вероятностью  мы можем ожидать, что значения с. в. z будут попадать в интервал
мы можем ожидать, что значения с. в. z будут попадать в интервал  .
.
Предполагая справедливость гипотезы 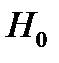 , вычислим значение
, вычислим значение 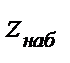 по данным выборки.
по данным выборки.
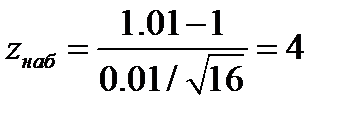
Наблюдаемое значение статистического критерия выходит за интервал принятия гипотезы. Нулевую гипотезу отвергаем. Статистические данные свидетельствуют о том, что фасовочная машина работает с нарушениями в настройке и математическое ожидание веса отдельного пакета отлично от заявленного.
Используя идеи, изложенные в примере 4, можно построить формальную процедуру сравнения выборочной средней с гипотетической генеральной средней нормальной совокупности. Для того чтобы при заданном уровне значимости 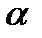 проверить нулевую гипотезу
проверить нулевую гипотезу  о равенстве генеральной средней
о равенстве генеральной средней  нормальной совокупности с известной дисперсией
нормальной совокупности с известной дисперсией  гипотетическому значению
гипотетическому значению  при конкурирующей гипотезе
при конкурирующей гипотезе 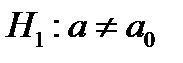 , надо вычислить наблюдаемое значение критерия:
, надо вычислить наблюдаемое значение критерия:

и по таблице функции Лапласа найти критическую точку двусторонней критической области 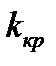 по равенству
по равенству

Если  — нет оснований отвергнуть нулевую гипотезу. Если
— нет оснований отвергнуть нулевую гипотезу. Если 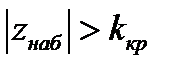 — нулевую гипотезу отвергают.
— нулевую гипотезу отвергают.
Если дисперсия генеральной совокупности неизвестна, то в качестве критерия проверки нулевой гипотезы принимают случайную величину:
 ,
,
которая имеет распределение Стьюдента с  степенями свободы. При конкурирующей гипотезе
степенями свободы. При конкурирующей гипотезе 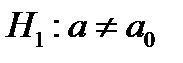 надо вычислить наблюдаемое значение критерия:
надо вычислить наблюдаемое значение критерия:
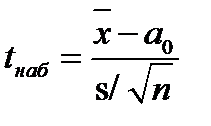
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости  , помещенному в верхней строке таблицы, и числу степеней свободы k найти критическую точку
, помещенному в верхней строке таблицы, и числу степеней свободы k найти критическую точку 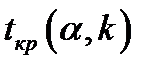 . Если
. Если  — нет оснований отвергнуть нулевую гипотезу. Если
— нет оснований отвергнуть нулевую гипотезу. Если  — нулевую гипотезу отвергают.
— нулевую гипотезу отвергают.
Пример 5. Используя статистические данные примеров 1 и 2 оценить диапазон возможных значений генеральной средней с. в. суточного водопотребления, обеспечивающих принятие двусторонней нулевой гипотезы при уровне значимости  .
.

Результат соответствует полученной ранее интервальной оценке математического ожидания.
Гипотеза о виде закона распределения. Критерий Пирсона.
Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид А, то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.
При использовании критерия Пирсона сравнивают эмпирические  (наблюдаемые) и теоретические
(наблюдаемые) и теоретические 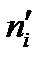 (вычисленные в предположении заданного распределения) частоты. В качестве статистического критерия проверки нулевой гипотезы примем случайную величину
(вычисленные в предположении заданного распределения) частоты. В качестве статистического критерия проверки нулевой гипотезы примем случайную величину  :
:
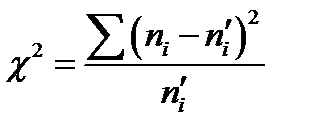
Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия  , и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
, и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
Доказано, что при 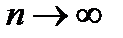 закон распределения случайной величины
закон распределения случайной величины  независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения  с
с 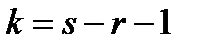 степенями свободы (
степенями свободы ( 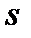 - число частичных интервалов выборки;
- число частичных интервалов выборки; 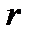 - число параметров распределения, которые оцениваются по данным выборки). В частности, если предполагаемое распределение нормальное, то оценивают два параметра – математическое ожидание и среднее квадратическое отклонение и
- число параметров распределения, которые оцениваются по данным выборки). В частности, если предполагаемое распределение нормальное, то оценивают два параметра – математическое ожидание и среднее квадратическое отклонение и  .
.
В критерии Пирсона используется правосторонняя критическая область  и область принятия гипотезы
и область принятия гипотезы  .
.
Для того чтобы при заданном уровне значимости проверить нулевую гипотезу о нормальном распределении генеральной совокупности, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
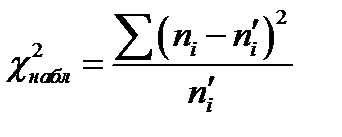
и по таблице критических точек распределения  по заданному уровню значимости
по заданному уровню значимости  и числу степеней свободы k = s — 3 найти критическую точку
и числу степеней свободы k = s — 3 найти критическую точку  .
.
Если  —нет оснований отвергнуть нулевую гипотезу.
—нет оснований отвергнуть нулевую гипотезу.
Если  —нулевую гипотезу отвергают.
—нулевую гипотезу отвергают.
Замечание 3. Объем выборки должен быть достаточно велик, во всяком случае, не менее 50 вариант. Каждая группа должна содержать не менее 5—8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.
Пример 6. По данным задач 1-3 выдвинуть и проверить гипотезу о нормальном законе распределения генеральной совокупности по методу Пирсона. По выборочным данным установить закон распределения с. в. суточного водопотребления и построить его график.
По результатам статистического анализа (задачи 1-3) можно выдвинуть статистическую гипотезу о нормальном виде распределения с. в. суточного водопотребления. Эта гипотеза подтверждается следующими соображениями.
1. Вид гистограммы плотностей относительных частот и кумулятивной кривой (задача 1). Эти графики служат оценкой по данным выборки кривых плотности распределения вероятностей и интегральной функции распределения соответственно. Для гистограммы плотностей относительных частот характерно наличие одного экстремума, симметричная относительно прямой, параллельной оси ОY, колоколообразная форма с убыванием ординат кривой при удалении от начала СК. Все это характерно для кривой плотности нормального распределения. Для кумулятивной кривой характерно наличие точки перегиба посредине области изменения возможных значений с. в. Левее точки перегиба кумулятивная кривая выпукла, правее – вогнута, что характерно для интегральной кривой нормального распределения.
2. Выполнение приближенного равенства 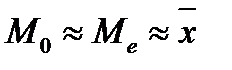 (задача 2), которое выполняется точно для нормального распределения.
(задача 2), которое выполняется точно для нормального распределения.
3. Величины асимметрии 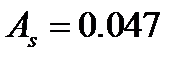 и эксцесса
и эксцесса 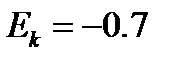 (задача 2). Известно, что абсолютные величины асимметрии и эксцесса показывают степень близости эмпирического распределения к нормальному.
(задача 2). Известно, что абсолютные величины асимметрии и эксцесса показывают степень близости эмпирического распределения к нормальному.

4. По правилу 3-х сигм. Теоретически, для нормального распределения:
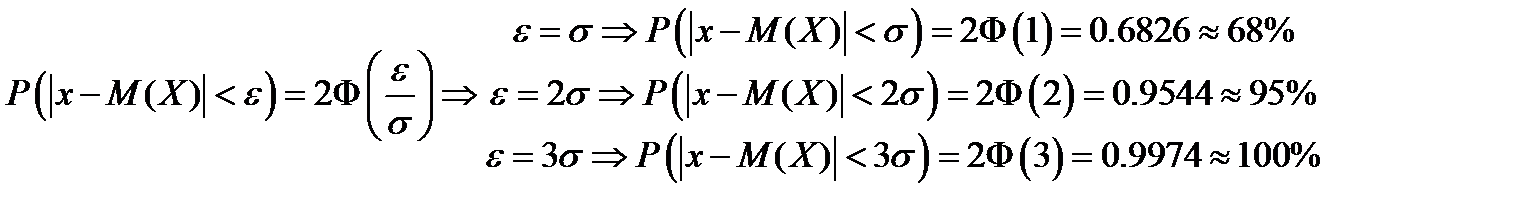
Данные выборки: в интервал 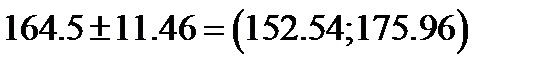 попадает
попадает  вариант;
вариант;
в интервал  попадает
попадает 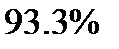 вариант; все варианты сосредоточены в интервале
вариант; все варианты сосредоточены в интервале 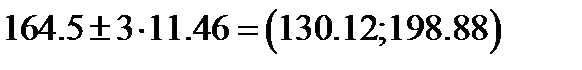 .
.
Для проверки гипотезы, 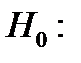 признак генеральной совокупности распределен по нормальному закону, надо найти теоретические частоты. Составим расчетную таблицу.
признак генеральной совокупности распределен по нормальному закону, надо найти теоретические частоты. Составим расчетную таблицу.
| Интервалы | Частоты  |  |  | 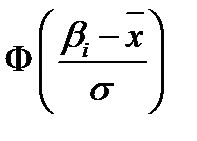 | 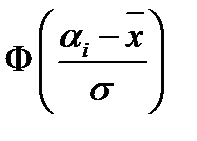 | 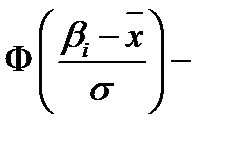 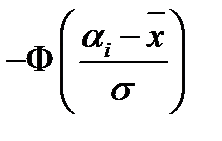 | 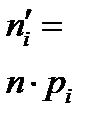 |
 | -1.5401 | -2.1567 | -0.4382 | -0.4886 | 0.0504 | ||
 | -0.9243 | -1.5401 | -0.3212 | -0.4382 | 0.117 | ||
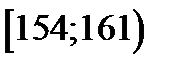 | -0.3081 | -0.9243 | -0.1217 | -0.3212 | 0.1995 | ||
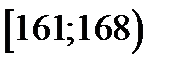 | 0.3081 | -0.3081 | 0.1217 | -0.1217 | 0.2434 | ||
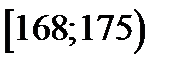 | 0.9243 | 0.3081 | 0.3212 | 0.1217 | 0.1995 | ||
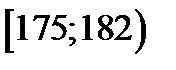 | 1.5401 | 0.9243 | 0.4382 | 0.3212 | 0.117 | ||
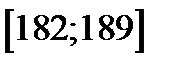 | 2.1567 | 1.5401 | 0.4846 | 0.4382 | 0.0504 | ||
| - | - | - | - | - |
 с. в. объема суточного водопотребления распределена по нормальному закону.
с. в. объема суточного водопотребления распределена по нормальному закону.
Аналитический вид функции плотности распределения вероятностей с. в. суточного водопотребления дается формулой:

Построим график теоретических вероятностей совместно с гистограммой плотностей относительных частот.

Лекция №5. Регрессионный анализ.
Уравнение регрессии. Коэффициент регрессии. Коэффициент корреляции и его свойства.
Две с. в. могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Оп. 1. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то этом случае статистическую зависимость называют корреляционной.
Пусть изучается система количественных признаков (X, Y). В результате  независимых опытов получены
независимых опытов получены  пар чисел
пар чисел 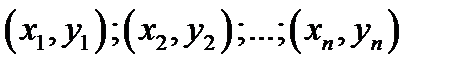 , причем значения признаков наблюдались по одному разу. Найдем по данным наблюдений выборочное уравнение прямой линии регрессии Y на X. Уравнение будем искать в виде
, причем значения признаков наблюдались по одному разу. Найдем по данным наблюдений выборочное уравнение прямой линии регрессии Y на X. Уравнение будем искать в виде 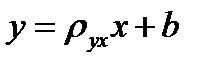 . Угловой коэффициент линии
. Угловой коэффициент линии  называют выборочным коэффициентом регрессии Y на X.
называют выборочным коэффициентом регрессии Y на X.
Подберем параметры  и
и 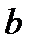 так, чтобы точки
так, чтобы точки 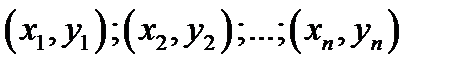 , построенные по данным наблюдений, на плоскости ХОY лежали как можно ближе к искомой прямой. этого требования. Назовем отклонением разность
, построенные по данным наблюдений, на плоскости ХОY лежали как можно ближе к искомой прямой. этого требования. Назовем отклонением разность 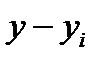 , где
, где 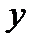 - вычислено по уравнению регрессии, а
- вычислено по уравнению регрессии, а 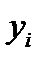 - наблюдаемая ордината. Подберем параметры
- наблюдаемая ордината. Подберем параметры  и
и 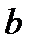 так, чтобы сумма квадратов отклонений была минимальной.
так, чтобы сумма квадратов отклонений была минимальной.