Мора кернеуінің диаграммасы 2 страница

Жоғарыдағы жағдайда сияқты (7.3) қатнасын өзара бір қатарлы және үздіксіз, яғни барлық аргументтері бойынша үздіксіз жеке туындылары бар деп санайтын боламыз.

Сірә, (7.1) және (7.3) формулары өзара кері функциялардың жалғыз жұбы түрінде ұсынылған және де, тұтас ортаны толтырған аймақтың әрбір нүктесіндегі мынандай функциональды анықтауш (якобион): 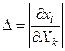(7.9)

нөльден айырмашылықта болады.

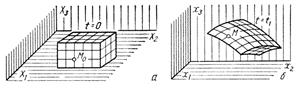
Бейнелеу. Көлемнің өзгеруі. Еркін бекітілген уақыт 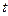-ның мәні үшін (7.1) және (7.2) функциялар жүйесі екі түрлі көзқараспен қаралуы мүмкін. Жоғарыда баяндалған біреуі бойынша олар байқаушының қозғалмайтын декарттық координат жүйесінде тұтас ортаның қозғалысын (деформациясын) бейнелейді.

Екінші көзқарас бойынша айтылған жүйелердің бірінші (7.1) жүйесі 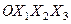декорттық координат жүйесімен жабдықталған үш өлшемді евклидов кеңістігінің кейбір D аймағын (7.3 сурет) 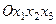декорттық координат жүйесімен жабдықталған екінші үш өлшемді евилидов кеңістігінің Е аймағына тегіс бейнелеуді анықтайды. Уақыттың әр түрлі мезгілінде 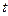дененің сырт пішінін анықтайтын бейнелеудің осындай тізбегі, тұтас ортаның қозғалысын және осы қозғалыспен байланысты деформацияны суреттейді. Бейнелеудің якобионы (7.9), осы бейнелеудің өте маңызды сипаттамасы болып саналады. Бейнелеу якобионының модулі қаралатын нүктедегі бейнелеудің бұрмалану коэффициенті болады. Осы коэффициент, шексіз кішкентай мөлшердің жоғарғы ретке дейінгі дәлдігімен, көрсетілген нүкте кіретін шексіз кішкентай аймақтың көлемі, оны бейнеленген кезде қанша рет өзгеретіндігін көрсетеді. (7.9) якобионы нөльге айналмайтындығы осыдан шығады. Тағыда айтатын нәрсе, ол бейнелеу уақытпен үздіксіз байланысты және бастапқы уақытта ( 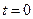) тепе-теңдікті бейнелеудің якобионы бірге тең болғандықтан, ол ылғида оң болады.

Ағымдағы көлемі 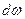және бастапқы көлемі 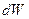болатын көлемдердің элементтері үшін мынандай қатнас орынды болады: 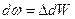. (7.10)

Қысылмау шартын мынандай түрде жазуға болады: 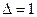. (7.11)

Осыған ұқсас 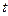бекітілген болған кезде (7.3) функциялар жүйесі Е аймағын D аймағына бейнелеуді анықтайды. Сонда мынаны жазуға болады: 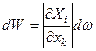. (7.12)

7.3 – сурет. Бейнелеу сияқты тұтас ортаның қозғалысы

Аффиндік бейнелеу. Сызықтық бейнелеудің мынандай түрін:

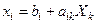(7.13)

аффиндік деп атайды. Аффиндік бейнелеу бүкіл 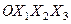кеңістігінде анықталған. Бейнелеудің якобионы, яғни 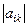анықтаушысы, кеңістіктің әрбір нүктесінде тұрақты мәнді сақтайды.

Аффиндік бейнелеу кез-келген сфераны эллепсоид етіп, ал жазықтық пен түзуді жазықтық және түзу етіп бейнелеумен жақсы.

Аффиндік бейнелеумен жазылатын деформацияланатын күй біркелке деп аталады.

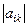тензорын диагональдық түрге келтірген кезде, бейнелеу жаңа координаттық осьтің бойымен біркелкі созуға (қысуға) келтірілетіндігі оқулық [1] жазылған (1.1 леммасы). Сонда (7.13) теңдеуі мынандай қарапайым түрді қабылдайды:

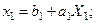
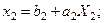
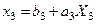. (7.14)

Әрбір дифференциалданатын бейнелеу жергілікті аффинді болып саналады. Сондықтан шексіз кішкентай аймақтағы аффиндік бейнелеу, барлық кеңістіктегі аффиндік бейнелеу ие болатын қасиетті иемденеді.

Сонымен, қозғалыс әрқашанда кейбір есеп беру жүйесіне, яғни координат жүйесіне қатысты анықталады. 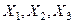коордианттары тікбұрышты декарттық координаттар жүйесінің координаттары болсын. Материальдық бөлшек Р-нің қозғалысын қарайық (7.1 сурет). Бастапқы кезде ( 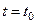уақтысында) осы бөлшек Р₀ 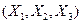орнын алады, 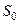бетімен шектелген бастапқы (деформацияға дейінгі) 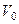көлемде орналасады. Ең ақырғы (деформацияланған) күйде осы бөлшек 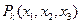жайын алады және 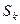бетімен шектелген 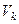деформацияланған көлемінде орналасады. Материалды бөлшек Р қозғалғанда, оның маңызды күйіне 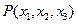бөлшегі сәйкес келеді және маңызды күй түсінігін барлық деформациялау процесінің нәтижесі де (түпкі күйі де) кіреді. Сөйтіп 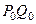, 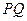және 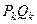дегеніміз бастапқы, маңызды және түпкі (нәтижелі) күйлердегі шексіз кішкентай бір материалды талшық. Егер бөлшек таңдалған координат жүйесіне қатысты қозғалса, онда оның 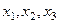координаттары 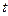уақытысы бойынша төмендегідей өзгереді: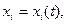

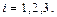
Қозғалатын материалды бөлшек уақыттың әр түрлі мезгілінде кеңістіктің әр түрлі нүктесіне келеді. Егер 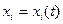функциясы белгілі болса онда материалды бөлшектің қозғалыс заңы белгілі болады.

Егер барлық материалды бөлшектің қозғалысы жазылған болса, онда тұтас ортаның ағатын немесе деформацияланатын қозғалыс заңы берілген болар еді. Ол үшін әрбір материалды бөлшекті жекеленген деп есептеу керек, яғни әрбір материалды бөлшекті бастапқы уақыт мезгілінде 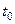нөмірлермен немесе бастапқы күй координаталары 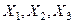–пен белгілеп қою керек. Онда тұтас ортаның қозғалысы, төрт айнымалы шамалар кіретін (7.1) формуласымен жазылады.

Егер (7.1) формуласында 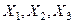координаттары бекітілген болса, онда тұтас ортаның барлық қозғалысынан жалғыз материалды бөлшектің қозғалысын ғана бөліп қарайтын боламыз. Егер 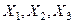координаттары әр түрлі болса, онда (7.1) функциясы бекітілген 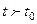уақыт мезгілінде материалды бөлшектердің кеңістікте таралуын анықтауға мүмкіндік береді. Осындай жағдайға материалды бөлшектер арасындағы ара қашықтықтың өзгеруі тіркелген болар еді. Сөйтіп (7.1) функциясы белгілі болса, онда тұтас ортаның деформация заңы берілген болады. Жоғарыда айтылған жағдайда деформация термині бастапқы және маңызды, соның ішінде түпкі (немесе нәтижелі) күйлерді салыстыруға қолданылады. Бірақта уақыт бойынша деформацияланудың тарихы қаралмайды. (7.1) теңдеуіндегі 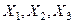координаттары және уақыт 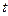Лагранж айнымалылары деп аталатындығын жоғарыда айттық. Тұтас ортадағы материалды бөлшектердің орын ауысуын төмендегі формуламен анықтайды: ағыс үшін 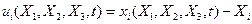; (7.15)

деформация үшін 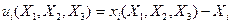(7.16)

Деформациаланатын қатты дене механикасындағы нақтылы есептерді шығарған кезде, іздейтін мөлшерлер болатын және континуумның қозғалыс заңына кіретін функциялар (7.1) үздіксіз және өзінің барлық аргументтері бойынша үздісіз жеке туындылары бар деп әдетте пайымдайды. Әрбір бекітілген уақыт мезгілінде (7.1) функциялары өзара бір қатарлы байланаста болуы керектігі физикалық түсініктен шығады. Себебі, олай болмайтын болса екі материалды бөлшек кеңістіктің бір нүктесіне бірдей баруы мүмкін. Сондықтан (7.1) теңдеулер жүйесінің жалғыз ғана шешімі бар болады. Осы шешім бойынша 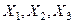координаттарын 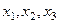координаттары және уақыт 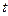функциясы ретінде (7.3) формуласымен анықтайды.

Деформацияға дейінгі жазықтықтар мен түзулер деформациядан кейін де жазықтар мен түзулер болып қалатын өте кішкентай кесіндіні, ауданды, көлемді деформацияланатын ортадан таңдап алуға болады. Осылай деформацияланатын ортада сфера эллипске айналатындығы бұрын айтылды. Осындай басқа түрге айналу сызықтық немесе аффиндік деп аталады. Аффиндік басқа түрге айналумен жазылатын деформациялық күй біркелкі деп аталады, ал (7.1) байланыстылығы (7.13) формуласымен жазылатын түрді алады.

Түрлендірудің якобионы (сызықтық немесе аффиндік түрлендірудің), яғни 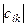аңықтаушысы нөльге тең болмайды және (7.13) теңдеулер жүйесіне сәйкесті, кеңістіктің әбден белгілі 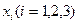нүктесіне ие болатың 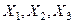координатасы бар әрбір жеке материалды бөлшек үшін тұрақты мәнді сақтайды. Демек, бекітілген уақыт мезгілі 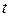және 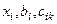белгілі мәндері үшін (7.13) теңдеулер жүйесін 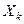белгісіздеріне қатысты шешіп мынандай функциональдық байланысты анықтауға болады: 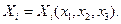(7.17)

Осыдан кейін ретті 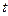-ның әр түрлі мәндері үшін ағу заңдарын (7.3) формуласы бойынша табуға болады.

(7.3) және (7.17) формуласындағы 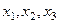координаталары және уақыт 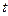Эйлер айнымалысы деп аталатындығы жоғарыда айтылды. Тұтас ортаның материалдық бөлшектерінің орын ауысуы мынандай формула бойынша жазылады: ағыс үшін

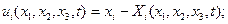(7.18)

деформация үшін 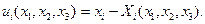(7.19)

Сонымен Лангранждық және Эйлерлік айнымалы шамалар бір ғана декорттық координаттар жүйесіне қатысты болады. Тұтас ортаның ағысын (7.15), (7.18) және деформациясын (7.16), (7.19) Лагранждық және Эйлерлік айнымалы шамалармен бейнелеудің арасындағы айырмашылық келесіден тұрады.

Тұтас ортаның ағысын және деформациясын (7.15) және (7.16) түрінде Лагранждық бейнелегенде, бастапқы уақыт 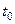мезгіленде координатасы 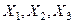болатын әрбір материалды бөлшектің қозғалысын бақылап отырады, яғни мұнда 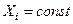. Әр түрлі уақыт 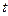мезгілінде тұтас ортаның деформациясын бейнелеу, әрбір материалды бөлшектің орын ауыстыру векторының теңдеуімен беріледі, және де .

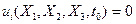Тұтас ортаның қозғалысын (7.18) және (7.19) түрінде Эйлерлік бейнелегенде кеңістіктің әрбір белгіленген нүктесінде болатынды бақылайды, яғни мұнда 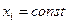. Деформациялау процесінде кеңістіктің белгіленген нүктесі арқылы әр түрлі материалды бөлшектер өтеді, яғни 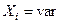. Сондықтан орын ауыстырудың шамасы уақыт бойынша өзгереді, бірақта .

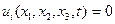Уақыт 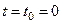мезгілінд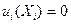е және 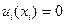теңдіктерінің бар болуы бастапқы уақыт t_о мезгілінде тұтас ортаның деформацияланбағынын, бастапқы орын ауыстырудың және кернеудің жоқтығын дәлелдейді.

Сонымен, Лагранждың көзқарасы бойынша зерттеушіні тұтас ортадан берілген жеке материалды бөлшектің жылдамдығының, үдеуінің, температурасының, кернеуінің, деформациясының және басқа мөлшерлерінің уақыт бойынша өзгеру заңдылықтары зауықтандырады. Ал Эйлердің көзқарасы бойынша зерттеушіні кеңістіктің нүктесінде (немесе нүктелерінде) жылдамдықтың, үдеудің, температураның, кернеудің және басқа мөлшерлердің уақыт бойынша өзгеру заңдылықтары зауықтандырады.

Негізгі әдебиеттер: [1] (тарау 2, бет 49 – 77). [4]: (тарау 3, бет 111 – 134).

Қосымша әдебиеттер: [6] (тарау 3, бет 38 – 58).

Бақылау сұрақтары:

1. Материальды бөлшектің лагранждық координатасы уақытпен өзгере ме?

2. Ілеспелі координат жүйесі дегеніміз не?

3. Кеңістік нүктесінің эйлерлік координатасы уақыт бойынша өзгере ме?

4. Лагранждық тәсілден Эйлерлік тәсіл немен айырмашылықта болады?

№8 дәріс. Түпкі деформацияның тензоры.

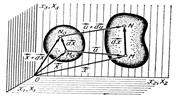
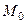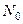Тұтас ортаның деформациясын бейнелеу мақсатымен екі жақын материалды бөлшектің орын ауыстыруын қарайық. Бастапқы мезгілде олар және нүктелерінде орын алсын (8.1 сурет), ал соңғы уақыт мезгілінд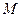е және 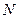нүктелеріне орын ауыстырсын.

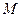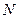және нүктелердің арасындағы шексіз кішкентай ара қашықтықтың еке есе дәрежесі мынаған тең: .

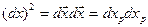Қозғалысты Лагранжша жазуды негіз етіп алайық. Оқулық [1] келтірілген формула бойынша мынаны жазуға болады: 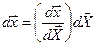немесе скалярлық түрде жазсақ мынаны аламыз: 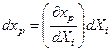. Нәтижесінде элемент ұзындығының екі есе дәрежесі мынаған тең болады: 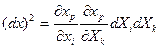(8.1)

Бастапқы уақыт мезгілендегі материалды бөлшектер арасындағы ара қашықтықтың еке есе дәрежесі мынаған тең болсын: 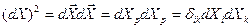, мұндағы 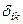– кронекер символы.

Бөлшектердің айналасындағы деформацияның өлшемі ретінде мынандай айырымды алайық:

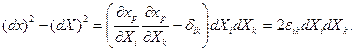(8.2)

Егер дененің барлық нүктелерінді мынандай шарт орындалса: 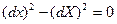, онда мұндай дененің қозғалысы мүлде қатты қозғалыс деп аталады. Егер дененің М нүктесіндегі инвариантқа мынандай шарт орындалса 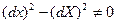, онда бұл нүктеде дене деформацияланған күйде деп айтылады.

8.1 – сурет. Көлем элементінің түпкі деформациясы

(8.2) теңдеуіндегі мынандай екінші рангілі тензорды: 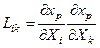(8.3)

Лангранждық түсініктегі Коши деформациясының тензоры деп атайды. Осы тензордың алты сыңарларының кейбіреуінің жайылған түрі мынандай болады:

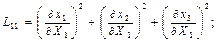
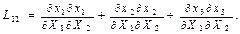
Екінші валентті симметриялық тензор мынандай сыңарларымен:

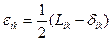(8.4)

немесе 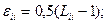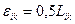түпкі деформацияның лагранждық тензоры (Грин тензоры) деп аталады.

Осы тензорды орын ауыстыру шамалары кіретін сыңарлары бар тензор түрінде көрсету ыңғайлы. Орын ауыстыру анықталатын мынандай формула жазайық: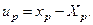

Жоғарыда жазылған формуладан мынаны табамыз: 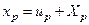. Алынған теңдеуді дифференциалдағаннан кейін мынаны аламыз:

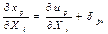және .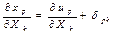

Екі соңғы формуларды (8.1) теңдеуіне қойып деформацияланған талшықтың (MN) модулінің екі есе дәрежесі мен орын ауыстырудың мынандай байланысын табамыз:

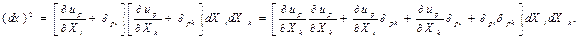
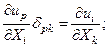
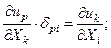
Мынандай теңдіктер орындылатын болғандықтан: 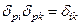төмендегі формуланы аламыз:

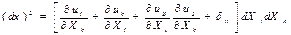. (8.5)

(8.2) және (8.5) формуларын салыстару мынаны жазуға мүмкіндік береді:

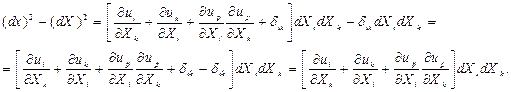(8.6)

Сонда, лангранждық түсініктегі Коши деформациясының тензорын орын ауыстыру арқылы мынандай түрде жазуға болады:

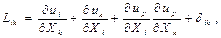(8.7)

ал Грин тензорының сыңарларын орын ауыстыру тензорының функциясы түрінде келесі қатнастар бойынша анықтайды:

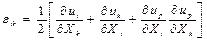. (8.8)

(8.8) формуласы түрінде жазылған Грин тензорының алты сыңарларының кейбіреуінің жайылған түрі мынандай болады:

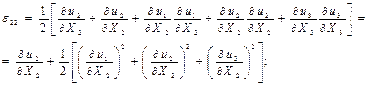
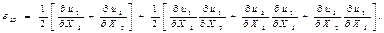
Қозғалысты эйлерлік түрде бейнелеуді негіз етіп алып деформация тензорлары сыңарларын анықтайтын формулаларды шығаруды қайталайық.

Оқулық [1] келтірілген формула бойынша мынаны жазуға болады: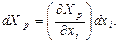

Нәтижесінде элемент ұзындығының екі есе дәрежесі мынаған тең болады:

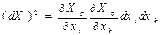. (8.9)

Ақырғы уақыт мезгіліндегі материалды бөлшектер арасындағы ара қашықтық еке есе дәрежесі мынаған тең: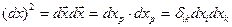

Бөлшектердің айналасындағы деформацияның өлшемі ретінде мынандай айырымды алайық:

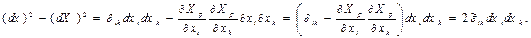(8.10)

Соңғы теңдеудегі мынандай екінші рангілі тензорды: 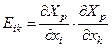(8.11)

Эйлерлік түсініктегі Коши деформациясының тензоры деп атайды. Сірә, 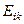–нің алты сыңарлары 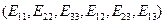жаңа симметриялық тензор құрайды және кейбіреуін мынандай формуламен анықтауға болады:

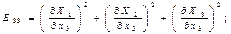
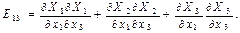
Мынандай сыңарлары бар екінші валентті симметриялық тензорды:

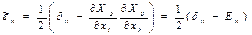(8.12)

немесе 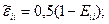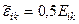түпкі деформацияның эйлерлік тензоры (Альмансы тензоры) деп атайды.

Жоғарыда жазылған әдістемені қолданып Альмансы тензорының сыңарларын орын ауыстыру арқылы анықтайтын болсақ мынаны аламыз:

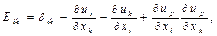(8.13)

ал Альманси тензорының сыңарларын орын ауыстыру тензорының функциясы ретінде келесі байланыстар бойынша анықтауға болады:

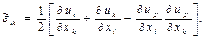(8.14)

Логарифмдік деформация. Әрбір 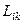және 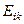симметриялық тензорлары үшін координат жүйесін бұрып (8.1) және (8.9) тензорлық эллипсоид теңдеулерін диагональды емес сыңарлары нөльге айналатын каноникалық түрге келтіруге болады. 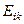және 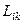тензорының мынандай диагональды түрге келтірілген 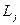және 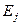сыңарлары: