Векторларға қолданылатын сызықтық амалдар

Сызықтық амалдар деп, векторларды қосу және алу, векторды санға көбейту амалдарын айтады.

Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.

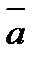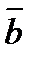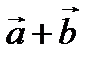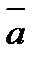Параллелограмм әдісі. және векторларының қосындысы деп, және 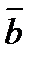векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.

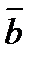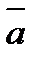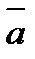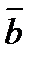Үшбұрыштар әдісі.Егер векторының басы векторының ұшына орналасса, онда және векторларының қосындысы 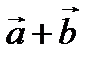деп, 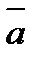векторының басы мен 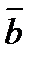векторының ұшын қосатын векторды айтады.

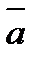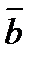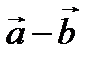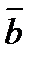Бір нүктеден шығатын және векторларының айырымы деп векторының ұшын 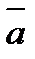векторының ұшымен қосатын векторды айтады.

№9

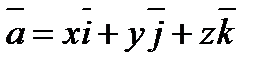вектордың координат өстерінің орттары арқылы жіктелген түрі деп аталады немесе қысқаша 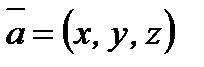деп жазады.

Екінші жағынан 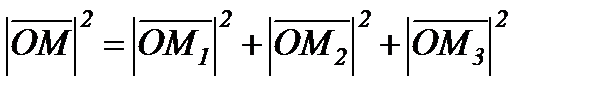= 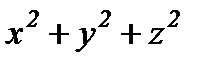, Осыдан 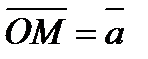болғандықтан 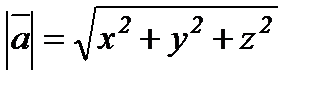- вектордың модулі (ұзындығы).

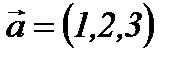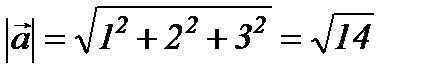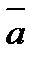, онда Егер векторы Ох, Оу, Oz өстерімен сәйкесінше 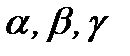бұрыштарын құрса, онда

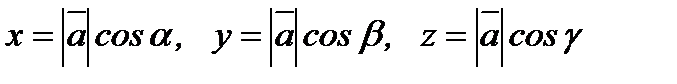, осыдан 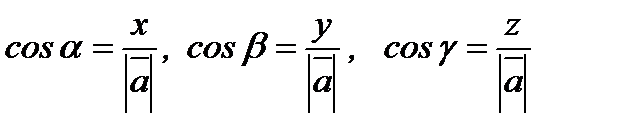болады. Мұндағы 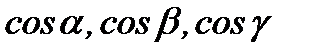сандары 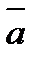векторының бағыттаушы косинустары деп аталады.

№10

Координаттарымен берілген векторларға амалдар қолдану

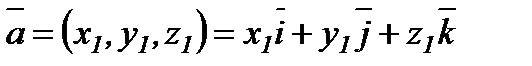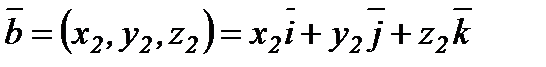, болса,

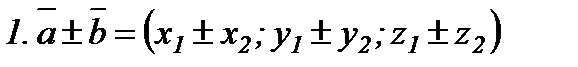
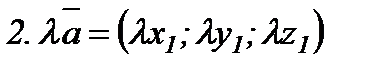
№11

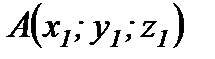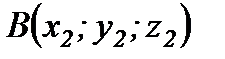Кесіндіні берілген қатынаста бөлу. және нүктелері арқылы өтетін кесінді берілсін. Осы кесіндіні 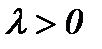қатынасындай етіп бөлетін 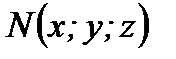нүктесінің координаттары: 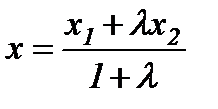, , 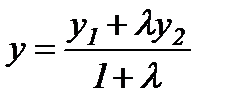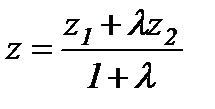- кесіндіні берілген қатынаста бөлу формулаларымен анықталады. Егер 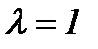болса, яғни 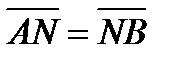онда

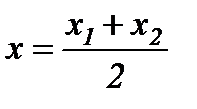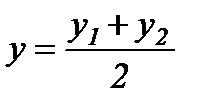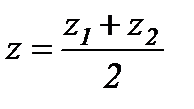, , - кесіндінің ортасын табу формуласы.

№12

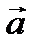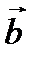Екі және векторларының скалярлық көбейтіндісі деп 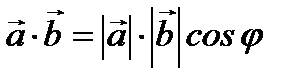санын айтады. Скаляр көбейтінді 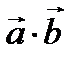, , 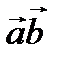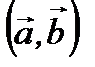символдармен белгіленеді.

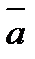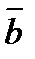және векторларының векторлық көбейтіндісі деп, келесі үш шартты қанағаттандыратын 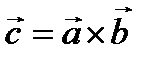векторын айтады:

1) ;

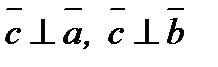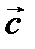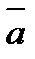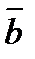2) векторының ұзындығы және векторларына тұрғызылған параллелограммның ауданына тең, яғни 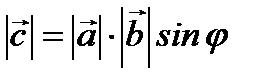, мұндағы ;

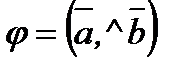3) 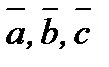векторлары оң үштік құрайды.

Векторлық көбейтінді 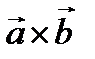немесе 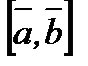деп белгіленеді.

Векторлық көбейтіндінің анықтамасынан 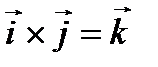, , 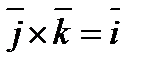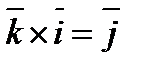болады

№13

Түзудің жалпы теңдеуі

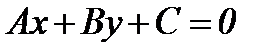
Түзудің бұрыштық коэффициент арқылы берілген теңдеуі.

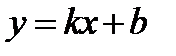
Екі нүкте арқылы өтетін түзудің теңдеуі.

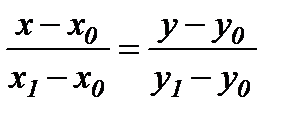
Түзудің кесінділік теңдеуі

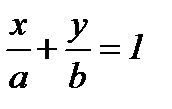
Берілген нүктеден өтетін түзудің теңдеуі

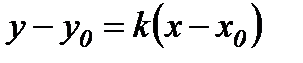
Екі түзудің арасындағы бұрыш.

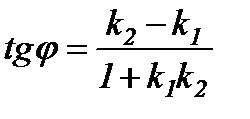
Нүктеден түзуге дейінгі қашықтық.

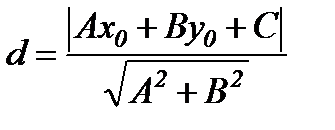
№14

Екі түзудің арасындағы бұрыш.

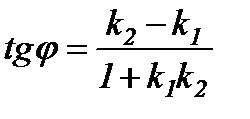
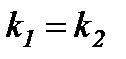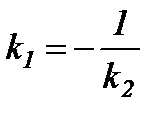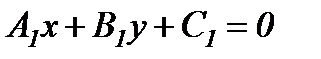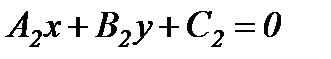Осыдан егер түзулер параллель болса, онда , ал түзулер перпендикуляр болса, онда болады. Түзулер және теңдеулерімен берілсе, онда 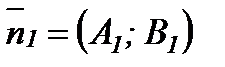, 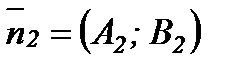болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:

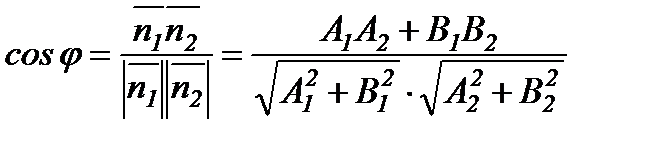(4.8)

Осыдан егер түзулер параллель болса, онда 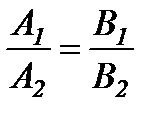, ал перпендикуляр болса, онда 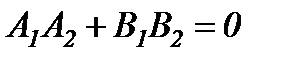болады.

№15

Ш нүкте арқылы өтетін жазықтықтың теңдеуі

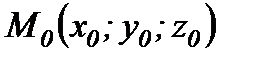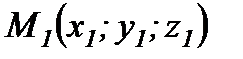, және 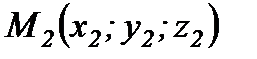нүктелері арқылы өтетін жазықтықтың теңдеуі:

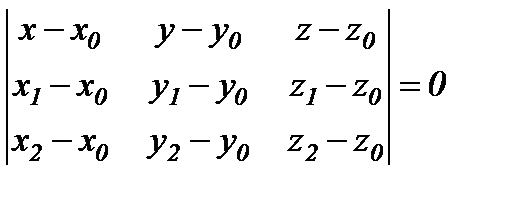
№16

Жазықтықтың жалпы теңдеуі

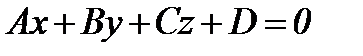
. Үш нүкте арқылы өтетін жазықтықтың теңдеуі. 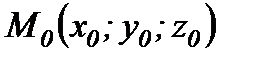, 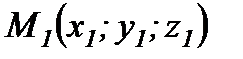және 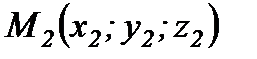нүктелері арқылы өтетін жазықтықтың теңдеуі:

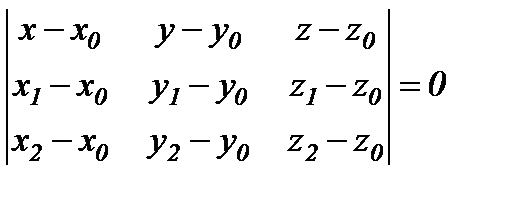
Жазықтықтың кесінділік теңдеуі

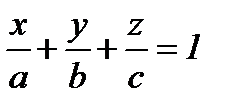
№17

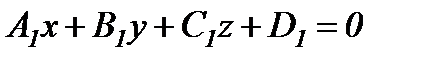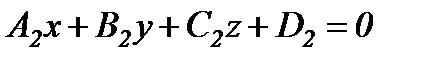Екі жазықтықтың арасындағы бұрыш. Жазықтықтар және теңдеулерімен берілсе, онда 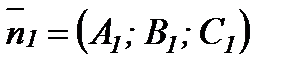, 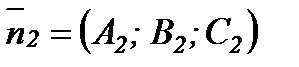болғандықтан жазықтықтардың арасындағы бұрыш осы екі нормальдің арасындағы бұ 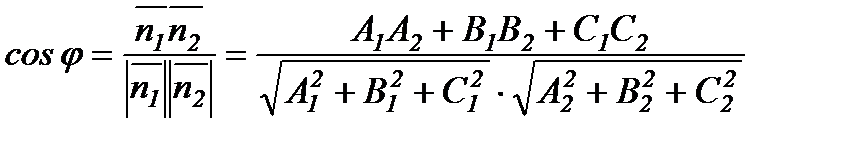(5.5)

Осыдан егер жазықтықтар параллель болса, онда 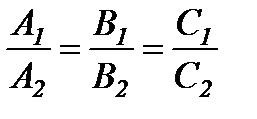, ал перпендикуляр болса, онда 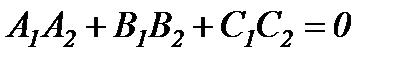болады.

№18

Нүктеден түзуге дейінгі қашықтық

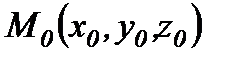нүктесінен 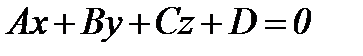түзуіне дейінгі қашықтықтың формуласы:

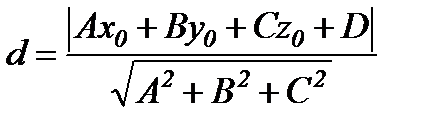
№19