Расчет статически определимого бруса.

КРУЧЕНИЕ.

Кручение, возникает при действии на стержень внешних сил, образующих момент, относительно оси стержня.

Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. При кручении в поперечном сечении возникает только один внутренний силовой фактор – крутящий момент Мкр.

Рассмотрим брус, нагруженный несколькими моментами.

Крутящий момент в произвольном сечении бруса численно равен алгебраической сумме внешних моментов, действующих по одну сторону от рассматриваемого сечения.

Дано: М1=1кНм, М2=3 кНм , М3=5кНм , М4=2 кНм , М5 =7 кНм

Mz Iучасток = М1=1кНм

Mz IIучасток = М1+M2=1+3=4кНм

Mz IIIучасток = М1+M2+M3=1+3+5=9кНм

Mz IVучасток = М1+M2+M3+M4=1+3+5-2=7кНм

Величину крутящего момента на различных участках бруса можно изобразить графически, построив так называемую эпюру крутящих моментов. Для этого под рисунком бруса располагаем ось абсцисс и от нее откладываем ординаты, изображающие величину крутящего момента.

Построив эпюру крутящих моментов можно найти величину крутящего момента в любом сечении.

Для определения напряжений можно воспользоваться методом сечений. Характер распределения напряжений по сечению выясним, рассмотрев геометрическую картину деформации вала при кручении.

При скручивании бруса круглого сечения происходит следующее:

Все образующие поворачиваются на один и тот же угол γ, а квадраты, нанесенные на поверхность бруса , перекашиваются , обращаясь в ромбы, т.е. подвергаются деформации сдвига. Каждое поперечное сечение поворачивается вокруг оси бруса на некоторый угол, называемый углом закручивания. Величина угла пропорциональна величине крутящего момента и расстоянию между сечениями.

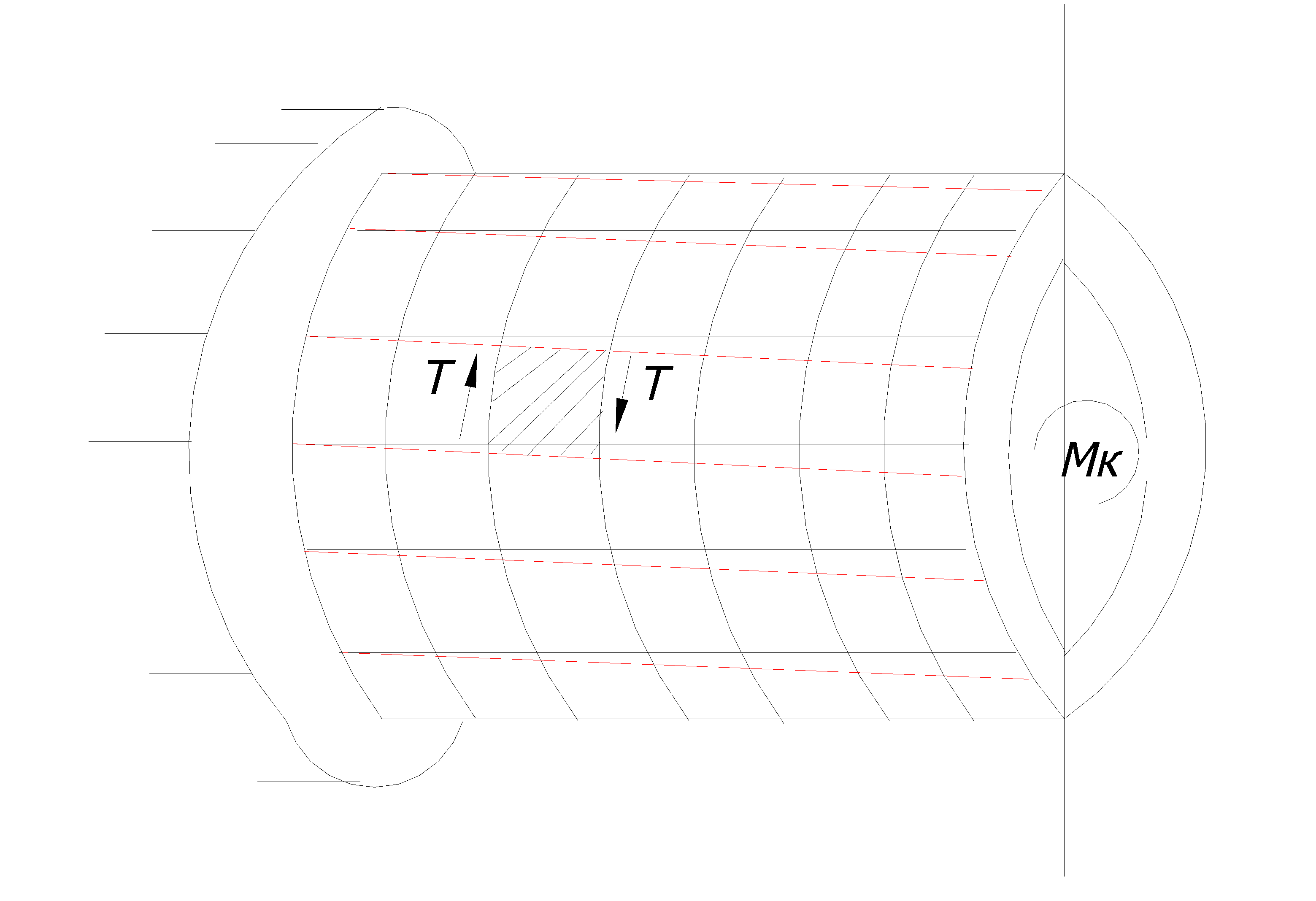
Расстояния между сечениями практически не меняются:

т.е. сечения поворачиваясь, относительно друг друга на угол Δφ, сохраняют расстояние между собой Δх.

Допущения.

1.Все поперечные сечения остаются плоскими.

2.Радиусы, проведенные в них, остаются прямыми (не искривляются).

3.Расстояния между сечениями не изменяются.

Рассмотрим статическую сторону задачи.

Т.к. Мкр – единственный внутренний силовой фактор в поперечном сечении , можно предположить, что здесь действуют только касательные напряжения. Интегральная зависимость:

τ - касательное напряжение, действующее на элементарной площадке dF, расположенной на расстоянии ρ от центра сечения.

Рассмотрим некоторый участок вала длиной dx . Вал подвержен действию крутящего момента Мк, вызывающего в поперечных сечениях внутренние крутящие моменты Мкр. Рассмотрим элемент авсd искажение формы элемента – случай деформации сдвига. Угол между образующими ав и ав' соответственно до и после деформации стержня называется относительным углом сдвига

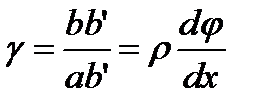
dφ /dx– относительный угол закручивания , имеет размерность см^-1, и обозначается Θ

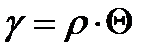
Угол сдвига прямо пропорционален расстоянию волокна от оси вала.

Рассмотрим связь между деформацией и напряжениями.

При кручении имеем деформацию сдвига, и по закону Гука при сдвиге

Подставляя это выражение в интегральную зависимость, получим:

Формула для определения относительного угла закручивания круглого стержня:

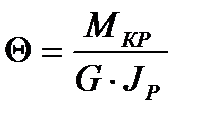
G∙J_P – жесткость сечения стержня на кручение, размерность кг∙см²

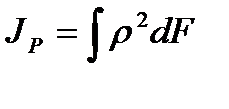
J_P– полярный момент инерции круглого стержня.

Полный угол закручивания стержня постоянного сечения длиной l

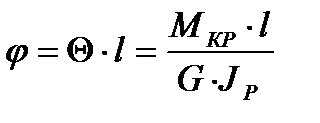
эта формула устанавливает связь между силовым фактором при кручении Мкр и соответствующей деформацией кручения (углом φ), представляет собой закон Гука при кручении.

Касательное напряжение в произвольной точке сечения определяется по формуле.

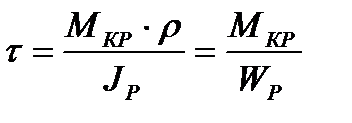
W_P – полярный момент сопротивления.

Для сплошного сечения круглого стержня:

Для трубчатого сечения круглого стержня:

;

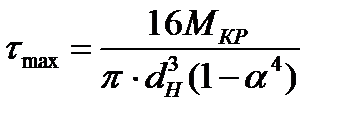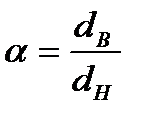
Максимальное касательное напряжение в скручиваемом круглом стержне пропорционально крутящему моменту Мкр и обратно пропорционально кубу наружного диаметра стержня.

Уравнение прочности при кручении

;

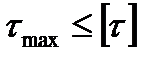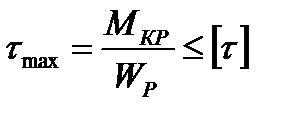
При проектировочном расчете:

Для круга

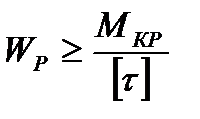
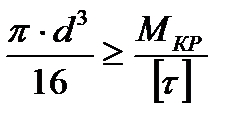
Для кольца

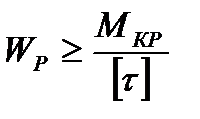
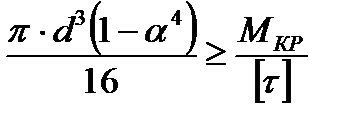
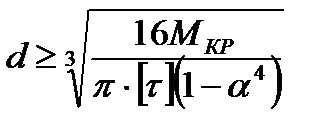
Вал, рассчитанный из условия прочности при проверке, может не удовлетворять условию жесткости

т.е. относительный угол Θ не должен быть больше допускаемого [Θ]

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОГО БРУСА.

Дано: М1=230кг∙м, М2=120 кг∙м, М3=550кг∙м

а = 0,4м, в = 0,15м, с = 0,3м , G =80000 МПа.

Для заданного стального бруса требуется:

1) Построить эпюру крутящих моментов М_КР

2) Определить из расчета на прочность диаметр каждого из участков бруса, принимая [τ]=60МПа

3) Построить эпюру наибольших касательных напряжений τ_МАХ

4) При принятых значениях диаметров построить эпюру углов поворота сечений

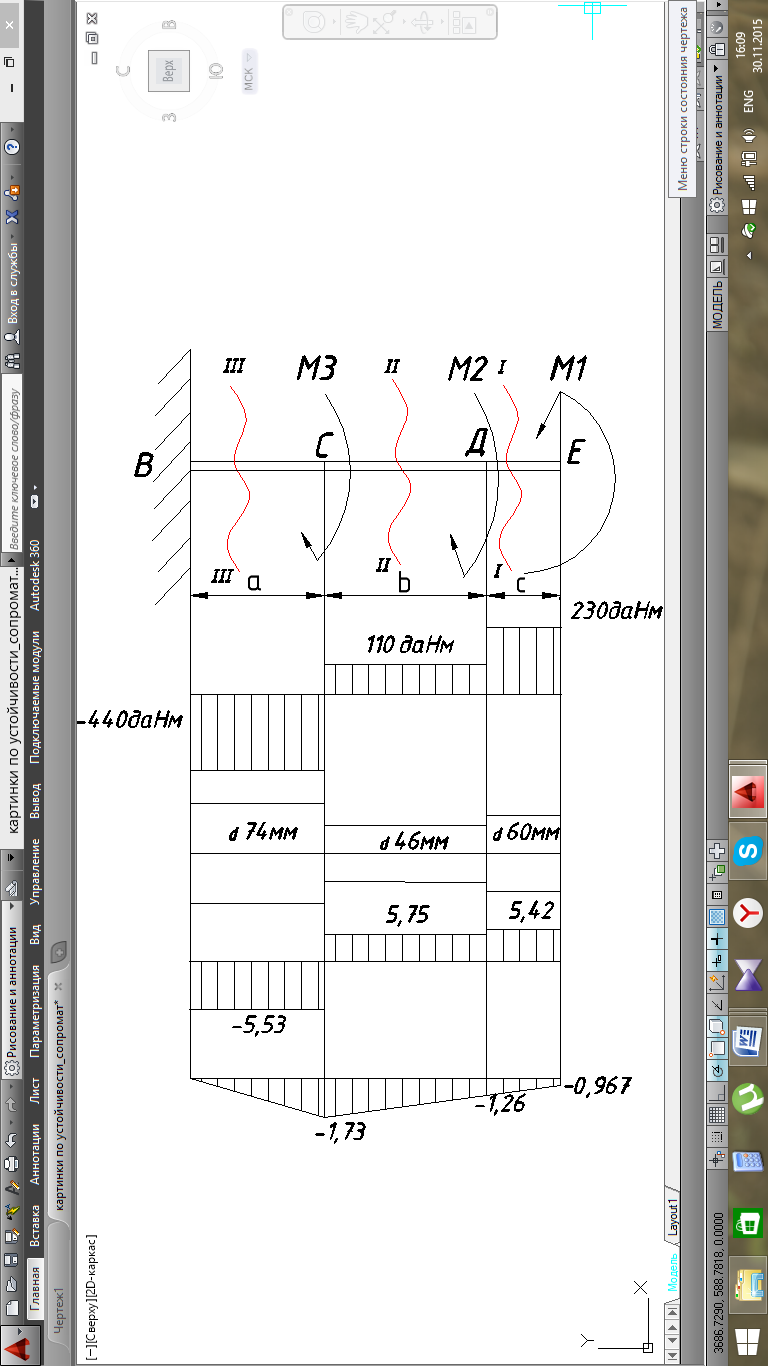
Эпюра крутящих моментов

Эпюра касательных напряжений

Эпюра углов поворота сечений

1.Определим значения крутящих моментов на участках бруса и построим эпюру Мкр= Мz :

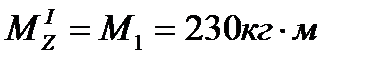
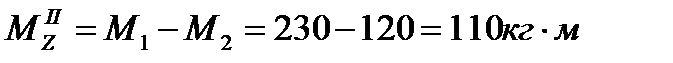
2. Определим диаметры каждого из участков бруса по формуле:

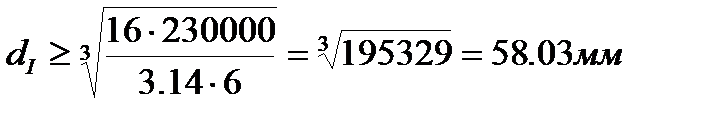
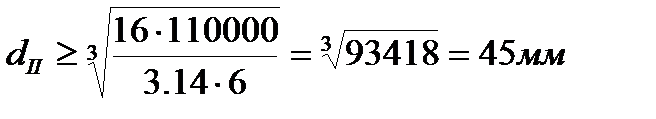
Принимаем d_I = 60мм

d_II = 46мм

d_III = 74мм

3. Определим значения наибольших касательных напряжений на участках бруса

и построим эпюру τ_МАХ

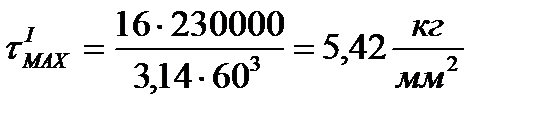
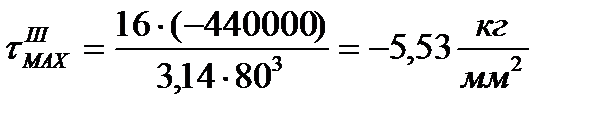
4. Определим значения углов поворота характерных сечений В, С, Д, Е

и построим эпюру φ

φВ = 0 ; φС = φВ + φВС=

φД = φС + φСД=

=

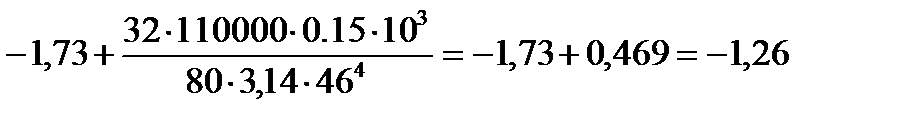
φЕ = φД + φДЕ=

=

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОГО БРУСА.

Для заданного бруса построить эпюры крутящих моментов и углов поворота поперечных сечений φ, если М1=М, М2=2,5М

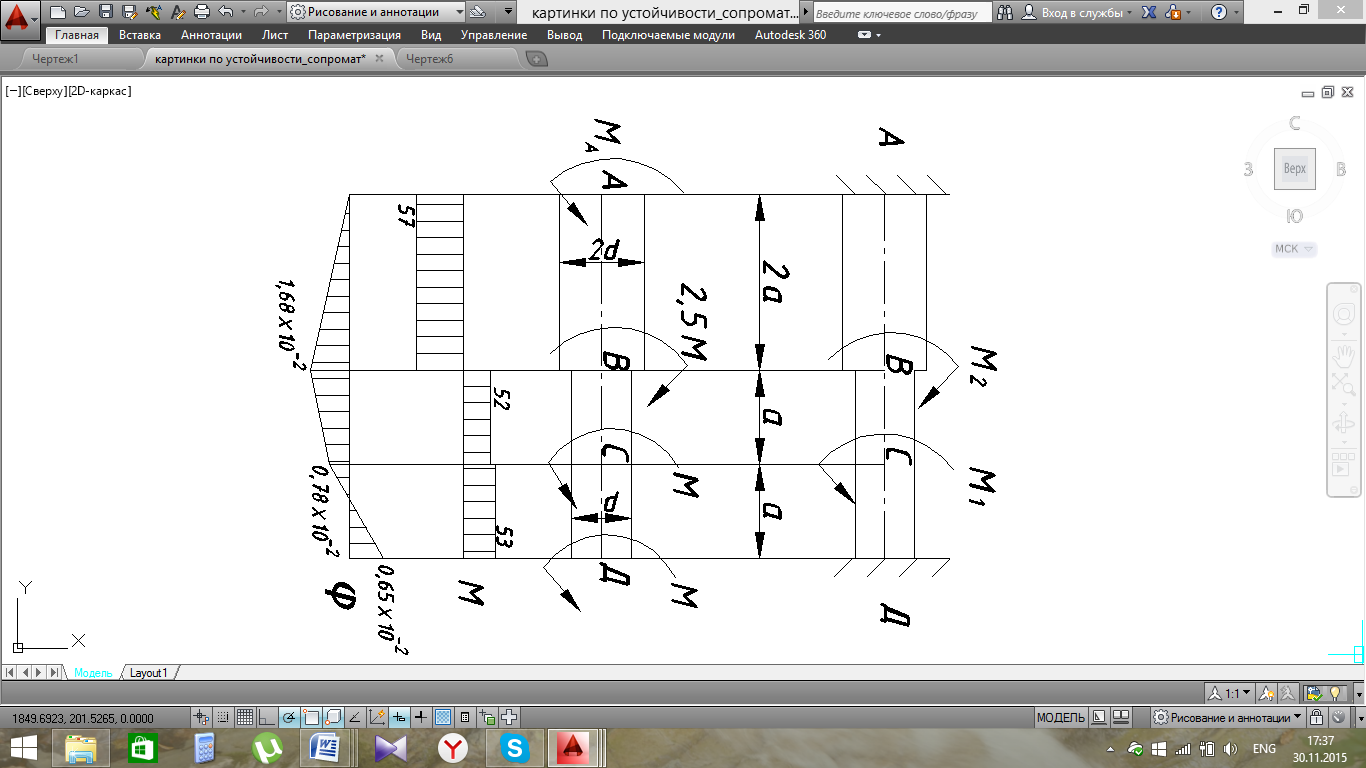
1.Отбросим связи, жестко защемленных опоры А и опоры Д. и заменим их реактивными моментами М_А и М_Д .

2.Для полученной системы внешних моментов статика дает 1 уравнение равновесия.

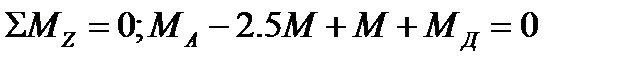
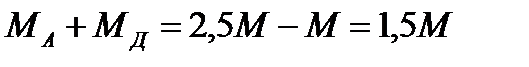(1)

Система 1 раз статически неопределима.

3.Составим уравнение совместности деформаций из условия отсутствия угла взаимного поворота концевых сечений.

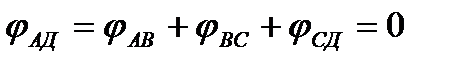(2)

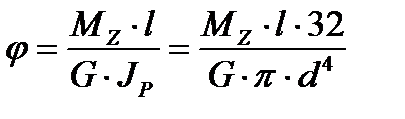
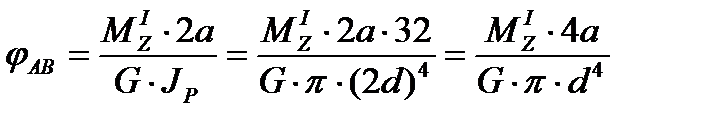(3)

(3)

(3)

4. Выражения (3) подставим в уравнение(2)

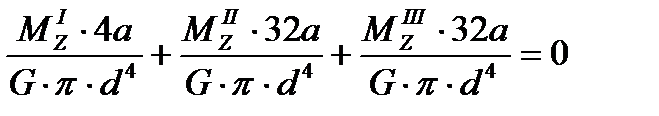
или

или

(4)

5. Определим крутящий момент.

(5)

(5)

(5)

6. Выражения (5) подставим в уравнение (4)

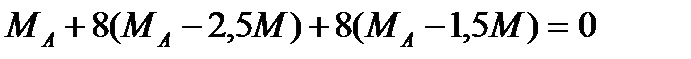
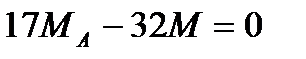
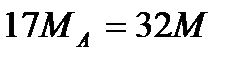
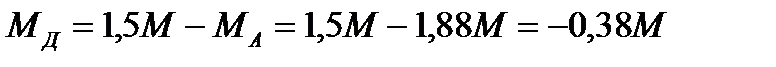
7. При известных М_А и М_Д определим крутящие моменты на участках бруса , учитывая выражения (5)

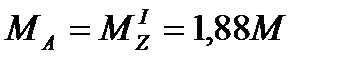
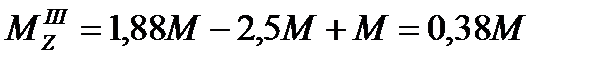
8. Определим значения углов поворота характерных сечений А, В, С, Д и построим эпюру φ

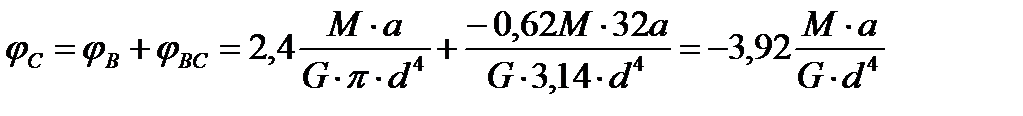
Проверка.