Неравенства Маркова и Чебышева

Неравенство Маркова. Если все значения случайной величины X неотрицательны, то вероятность того, что она примет значение, превосходящее заданное число Q > 0, удовлетворяет неравенству Маркова:

Определение 33. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Определение 34. Областью принятия гипотезы называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Определение 35. Критическими точками (границами) К_кр называют точки, определяющие критическую область от области принятия гипотезы.

Определение 36. Правосторонней (левосторонней) называют критическую область, определяемую неравенством К > К_кр, где К_кр > 0 (К < К_кр, К_кр < 0).

Определение 37. Двусторонней называют критическую область, определяемую неравенствами K < К₁, K > К₂, где K₂ > K₁. В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенствами (причем K_kp > 0):

К < – К_кр, , K > К_кр, то есть |K| > К_кр.

Для отыскания критической области задаются уровнем значимости 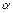и ищут критические точки, исходя из следующих соотношений:

а) для правосторонней критической области

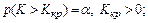
б) для левосторонней критической области

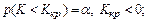
в) для двусторонней симметричной области

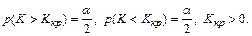
Определение 38. Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза (то есть нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза).

Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями (зависимые выборки).

Пусть 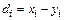- разности вариант с одинаковыми номерами.

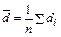- средняя разностей вариант с одинаковыми номерами.

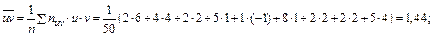и, следовательно, выборочный коэффициент корреляции

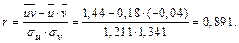
6. Находим выборочный коэффициент регрессии и параметр b:

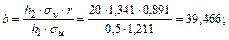
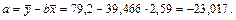
7. На основе полученных результатов запишем выборочное уравнение регрессии Y на X

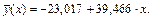
8. Поскольку выборочный коэффициент корреляции с точностью до сотых r = 0,89, то между X и Y линейная корреляционная связь очень тесная.

Статистические гипотезы

Определение 26. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Определение 27. Нулевой (основной) называют выдвинутую гипотезу H₀.

Определение 28. Конкурирующей (альтернативной) называют гипотезу H₁, которая противоречит нулевой.

Различают гипотезы, которые содержат одно и более одного предположений.

Определение 29. Простой называют гипотезу, содержащую только одно предположение.

Определение 30. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

В итоге проверки гипотезы могут быть допущены ошибки 2-х родов.

Ошибка 1-го рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки 1-го рода называется уровнем значимости a.

Ошибка 2-го рода состоит в том, что будет принята неправильная нулевая гипотеза и обозначается через b.

Определение 31. Статистическим критерием (просто критерием) называют случайную величину K, которая служит для проверки гипотезы.

Определение 32. Наблюдаемым значением К_набл. называют то значение критерия, которое вычислено по выборкам.

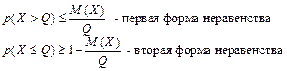(16)

Неравенство Маркова используется при решении задач, если известно или может быть рассчитано математическое ожидание. При наличии или возможности получения информации о дисперсии следует также рассмотреть неравенства:

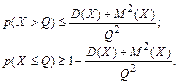(17)

После сравнения результатов (16) и (17) в ответ следует записать более значимый из них.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине превзойдет заданное положительное число e, удовлетворяет неравенству:

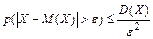- первая форма неравенства;

(18)

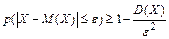- вторая форма неравенства.

Неравенство Чебышева используется при решении задач, если известна или может быть рассчитана дисперсия и искомый интервал значений случайной величины Х или возможный интервал вне искомого имеет границы симметричные относительно математического ожидания.