Диференціальні та різницеві рівняння

1) Що таке диференціальне рівняння? Як визначається його порядок?

2) Який загальний вигляд ДР 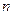–го порядку? Його канонічний (нормальний) вигляд?

3) Що називається розв’язком ДР?

4) Що таке інтегральна крива ДР?

5) Що називається загальним розв'язком ДР? Частинним роз­в’язком? Який їх геометричний зміст?

6) Що таке початкові та крайові умови? Як ставиться початкова задача (задача Коші)? Крайова задача?

7) Що таке особливий розв'язок ДР?

8) Як для ДР першого порядку формулюється теорема Коші (існування та єдиності розв'язку)? У чому її геометричний зміст?

9) Яке ДР 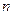-го порядку називається лінійним однорідним? Лінійним неоднорідним?

10) Яка система функцій 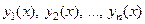називається лінійно залежною? Лінійно незалежною?

11) Сформулюйте ознаку лінійної залежності чи незалежності системи 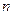частинних роз­в’яз­ків 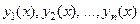одного ЛОДР 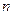-го порядку.

12) Яка структура загального розв’язку ЛОДР другого порядку?

13) Що таке характеристичне рівняння для ЛОДР другого порядку зі сталими коефіцієнтами?

14) За якими формулами будується загальний розв’язок ЛОДР другого порядку зі сталими коефіцієнтами в залежності від виду коренів характеристичного рівняння?

15) Яка структура загального розв’язку ЛНДР другого порядку?

16) У чому полягає принцип суперпозиції розв’язків ЛНДР?

17) Як будується розв'язок ЛНДР другого порядку методом варіації довільних сталих?

18) Для ЛНДР що таке права частина спеціального вигляду?

19) Як методом невизначених коефіцієнтів будується частинний розв'язок ЛНДР другого порядку зі сталими коефіцієнтами, що відповідає правій частині спеціального вигляду?

Лінійна та векторна алгебра. Аналітична геометрія в просторі.

Функції багатьох змінних

1) Що називається визначником?

2) Що таке мінор і алгебраїчне доповнення елемента визнач­ника?

3) За яким правилом обчислюється значення визначника 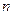-го порядку?

4) Сформулюйте правила “хреста” і “трикутників” для обчис­лення відповідно визначників другого і третього порядку.

5) Сформулюйте основні властивості визначника.

6) Як знаходиться значення визначника трикутного вигляду?

7) Що називається матрицею?

8) Яка матриця називається невиродженою?

9) Як здійснюються операції додавання (віднімання) матриць і множення матриці на число? Чим відрізняється множення матриці на число від множення визначника на число?

10) Як здійснюється операція множення матриць? Які власти­вості цієї операції?

11) Що таке обернена матриця та як вона обчислюється?

12) Що називається рангом матриці?

13) Як знаходиться ранг матриці методом обвідних мінорів?

14) Які операції називаються елементарними перетвореннями матриці?

15) Які матриці називаються еквівалентними?

16) Як знаходиться ранг матриці методом елементарних пере­творень?

17) Який вигляд має система 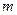лінійних алгебраїчних рівнянь (СЛАР) з 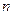невідомими?

18) Яка система називається сумісною? Визначеною?

19) Сформулюйте теорему Кронекера – Капеллі для лінійних систем.

20) Як знаходиться розв’язок квадратної СЛАР за допомогою оберненої матриці?

21) Як розв’язується квадратна СЛАР методом Крамера?

22) Як розв’язується довільна СЛАР методом Гаусса?

23) Сформулюйте умову наявності в квадратної СЛАР нену­льових розв’язків.

24) Як використовуються блочні матриці для розвязування СЛАР і знаходження оберненої матриці?

25) Як задається прямокутна система координат у просторі? Як утворюється координатна сітка цієї системи координат?

26) Що таке скалярні та векторні величини?

27) Які вектори називаються колінеарними? Компланарними? Рівними?

28) Як знаходяться сума, різниця двох векторів і добуток век­тора на число?

29) Як знаходяться проекція вектора на ненульовий вектор?

30) Що таке координати вектора? Як здійснюються лінійні опе­рації над векторами в координатній формі?

31) Як знаходяться модуль і напрямні косинуси вектора, зада­ного в координатній формі?

32) Як формулюється умова колінеарності двох векторів?

33) Як знаходяться координати точки, що ділить відрізок у да­ному відношенні?

34) Що називається скалярним добутком двох векторів? Як він обчислюється в координатній формі?

35) У чому полягає умова ортогональності двох векторів?

36) Що називається векторним добутком двох векторів? Як він обчислюється в координатній формі?

37) У чому полягає геометричний зміст векторного добутку?

38) Що називається мішаним добутком трьох векторів? Як він обчислюється в координатній формі?

39) У чому полягає геометричний зміст мішаного добутку?

40) У чому полягає умова компланарності трьох векторів?

41) Яка трійка векторів утворює базис? Як знайти координати вектора в даному базисі?

42) Що називається 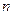-вимірним векторним простором? Який простір є лінійним?

43) Яка система векторів називається лінійно незалежною?

44) Що таке базис 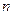-вимірного векторного простору?

45) Що називається лінійним відображенням? Що таке матриця лінійного відображення?

46) Як задаються паралельне перенесення і поворот прямокутної системи координат на площині?

47) Що таке власні числа і власні вектори квадратної матриці?

48) Як знаходяться власні числа і власні вектори?

49) Сформулюйте властивості власних чисел і власних векторів.

50) Що таке матричний многочлен?

51) Сформулюйте теорему Келі – Гамільтона про характерис­тичний многочлен.

52) Як розв’язується СЛАР методом простих ітерацій?

53) Наведіть основні типи рівняння площини.

54) Як обчислюється кут між площинами?

55) Сформулюйте умови паралельності та перпендикулярності двох площин.

56) Як обчислюється відстань від точки до площини?

57) Наведіть основні типи рівняння прямої у просторі.

58) Як обчислюється кут між прямими у просторі?

59) Сформулюйте умови паралельності та перпендикулярності двох прямих у просторі.

60) Як обчислюється кут між прямою і площиною?

61) Сформулюйте умови паралельності та перпендикулярності прямої та площини.

62) Як знаходиться відстань між непаралельними прямими?

63) Як знаходиться відстань від точки до прямої у просторі?

64) Яка поверхня називається сферою? Наведіть канонічне рівняння сфери та рівняння сфери зі зміщеним центром.

65) Запишіть загальне рівняння поверхні другого порядку.

66) Яка поверхня називається циліндричною? Запишіть канонічні рівняння еліптичного, гіперболічного, параболічного циліндрів.

67) Яка поверхня називається конічною? Наведіть канонічне рівняння конуса другого порядку.

68) Як утворюється поверхня обертання? Як знайти рівняння по­верхні, утвореної обертанням заданої кривої, що лежить у коор­динатній площині, навколо однієї з координатних осей цієї ж площини?

69) Запишіть канонічні рівняння еліпсоїда, однопорожнинного і двопорожнинного гіперболоїдів, еліптичного та гіперболічного параболоїдів. Які з цих поверхонь є лінійчатими?

70) Наведіть означення функції 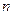змінних та її області визначення.

71) Як знайти природну область визначення (область допустимих значень) функції багатьох змінних?

72) Дайте означення функції двох змінних та її області визначення. Який геометричний зміст цих понять? Наведіть приклади графіків функцій двох змінних.

73) Що називається лінією рівня функції двох змінних? Поверхнею рівня функції трьох змінних? Наведіть приклади ліній та по­верхонь рівня.

74) Дайте означення границі та неперервності функції 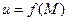в точці.

75) Запишіть вирази для повного та частинних приростів функції 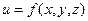в точці .

76) Наведіть означення частинних похідних функції багатьох змінних. У чому полягає геометричний зміст частинних по­хідних функції двох змінних?

77) Як за правилами диференціювання функції однієї змінної знаходяться частинні похідні функції багатьох змінних?

78) Що таке частинні та повний диференціали функції 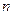змінних?

79) Сформулюйте необхідні та достатні умови диференційовності функції двох змінних.

80) У чому полягає інваріантність форми повного диференціала?

81) Як застосовується повний диференціал у наближених обчисленнях?

82) За якими формулами проводиться диференціювання складених функцій багатьох змінних? Запишіть формулу повної похідної.

83) За якими формулами проводиться диференціювання неявно заданих функцій однієї і двох змінних?

84) Дайте означення похідних і диференціалів вищих порядків.

85) Сформулюйте умови незалежності мішаної частинної похідної від порядку диференціювання.

86) Наведіть означення дотичної площини і нормальної прямої до поверхні.

87) Запишіть загальне рівняння дотичної площини і канонічні рівняння нормальної прямої до поверхні, що задана явно. Який вигляд набувають ці рівняння у випадку неявного задання поверхні?

88) У чому полягає геометричний зміст повного диференціала функції двох змінних?

89) Дайте означення похідної за напрямом і градієнта функції трьох змінних.

90) Запишіть формули для обчислення похідної за напрямом і градієнта у прямокутних координатах.

91) Як зв’язані похідна за напрямом і градієнт, градієнт і вектор нормалі до поверхні рівня?

92) Наведіть означення точки локального мінімуму (максимуму) функції багатьох змінних.

93) Сформулюйте необхідні умови локального екстремуму.

94) Яка точка називається стаціонарною?

95) Сформулюйте достатні умови локального екстремуму функції двох змінних.

96) Як ставиться задача на умовний екстремум для функції двох змінних?

97) У чому полягає метод множників Лагранжа для знаходження умовного екстремуму функції двох змінних?

98) Як знаходяться найменше та найбільше значення функції двох змінних у замкненій області?