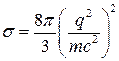Рассеяние света на свободных зарядах. Формула Томсона. Пусть свободный заряд находится в поле плоской монохроматической волны

Пусть свободный заряд находится в поле плоской монохроматической волны 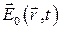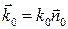. Под действием поля заряд придет в неравномерное прямолинейное движение 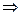будет излучать вторичные волны рассеивание первичной волны.

Поток энергии через векторную площадку 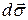, стягивающую телесный угол 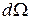, т.е.

.

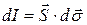Если волна имеет плотность потока энергии

,

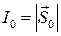а поток энергии вторичной волной в направлении 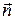в телесный угол :

,

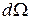где 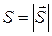, то величину 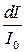- дифференциальное эффективное сечение рассеяния, 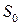- вектор пойтинга волны .

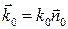Реально измеряются лишь энергетические величины усреднённые по промежуткам времени чем период. Поэтому эффективное дифференциальное сечение определяет отношение таких средних

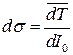, где 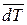- усреднение по времени

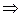т.к. , .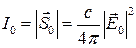

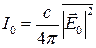В рассеянной волне будем учитывать лишь электрическую дипольную часть

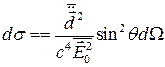
Установим связь между ,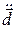

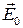
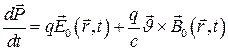
Учитывая, что в дипольном приближении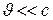

Соответственно:

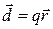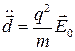, , откуда

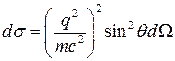
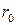, - классический радиус электрона.

Здесь 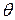- угол между направлением рассеяния 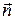и направлением поляризации .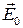

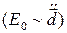Пусть волна распространяется вдоль оси 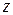. Рассеяние происходит вдоль плоскости

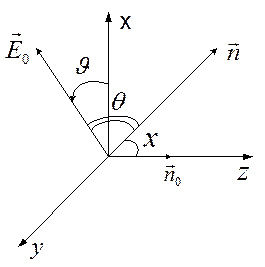
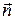- направление рассеяния волны.

Направление поляризации, лежащее в плоскости отклонено от 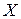на . Если обозначить через 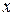угол рассеяния, то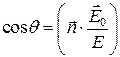

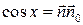
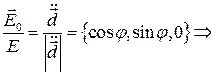
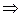
Эффективное дифференциальное рассеяние.

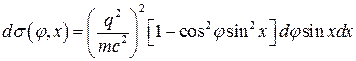
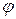задаёт ориентация поляризации плоско-поляризованной волны.

Свет от естественных источников редко обладает определённой поляризацией. Он обладает плоскополяризованной волной, направленной по разному не когерентных между собой. Складываются энергии, а не поля 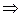усреднить по всем .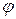

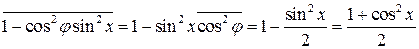
Поэтому для неполяризованной волны:

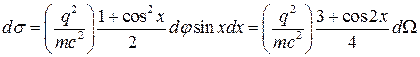
Полное эффктивное сечение рассеяния на свободном заряде получается интегрированием по углам и приводит к формуле Томсона: