Теоретический материал. Пусть известна вероятность появления события А в одном испытании:
Пусть известна вероятность появления события А в одном испытании:
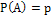, причем 
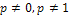, тогда 
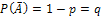- вероятность непоявления события А.
Испытание повторяются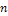 
раз. Какова вероятность того, что событие А наступит при этом 
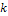раз?
Эта вероятность находится по формуле Бернулли:
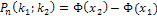, где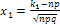 
, 
.
,
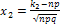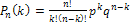где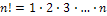 
например 
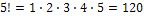. Запомните, что 
, как и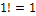 
.
Формулу Бернулли удобно применять, если число повторных испытаний невелико (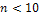 
).
Если число испытаний велико (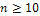 
), то вместо формулы Бернулли используется так называемая локальная формула Лапласа, которая является приближенной:
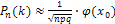, где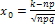 
.
Значение функции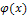 
берется из таблицы, (см. приложение 1).
Если число испытаний велико ( 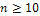) и нужно найти вероятность наступления события А в каждом из 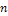независимых испытаний постоянна и отлична от 0 и 1, то применяют интегральную формулу Лапласа, которая также является приближенной:
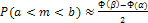, где 
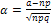и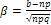 
.
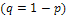Значения функции Лапласа Ф берутся по таблице. (см. приложение 2).
В 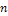повторных испытаниях событие А может наступить: 0; 1; 2;...; 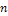раз (то есть 
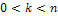). Дня каждого из этих чисел можно найти соответствующую ему вероятность по формуле Бернулли или Лапласа. То из чисел, которому соответствует самое большое значение вероятности, называется НАИВЕРОЯТНЕЙШИМ числом появления события А. Наивероятнейшее число 
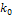находится как целое число из промежутка:
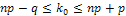
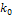может принимать либо одно значение, либо два соседних целых значения, когда вероятность их одинаковы.
Вероятность появления события хотя бы один раз в 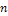испытаниях находится с помощью противоположного события
.
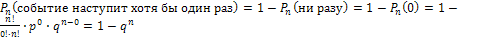