Iнтерполяцiйна формула Лагранжа

Інтерполяційні методи наближення функцій однієї та двох змінних.

Метою вивчення цього роздiлу є ознайомлення з основними найбiльш вживаними методами iнтерполяцiї функцiй однiєї та двох змiнних.

Постановка задачi iнтерполяцiї функцiй однiєї змiнної

В обчислювальнiй практицi часто доводиться мати справу з функцiями , заданими таблицями їх значень для деякої скiнченної множини значень аргумента : , , , . В процесi ж розв'язування задачi необхiднi промiжнi значення функцiї, яких немає в таблицi. В цьому випадку будують функцiю , досить просту для обчислень, яка в заданих точках приймає тi ж значення, що i функцiя , а в iнших точках розглядуваного iнтервалу iз областi визначення функцiї дає наближення функцiї з певною точнiстю, i при розв'язуваннi задачi замiсть функцiї оперують з функцiєю .

Задача побудови такої функцiї ,яка задовольняє умови називається задачею iнтерполяцiї (вiд inter --- мiж i pol --- полюс, точка). Функцiя називається iнтерпольованою функцiєю, а iнтерполюючою функцiєю або iнтерполянтом.

Точки називаються вузлами iнтерполяцiї.

Геометрично задача iнтерполяцiї полягає в побудовi кривої певного типу, яка проходить через задану систему точок , .

Частiше всього iнтерполюючу функцiю шукають у виглядi алгебраїчного многочлена.

Iнтерполяцiйна формула Лагранжа

Нехай функцiя задана таблицею значень , . Треба побудувати многочлен степеня не вище , який приймає в вузлах iнтерполяцiї тi ж значення, що i , тобто многочлен, для якого виконуються рiвностi , .

Розв'язком цiєї задачi є iнтерполяцiйний полiном Лагранжа:

(1)

Iнтерполяцiйна формула в цьому випадку має вигляд:

(2)

i називається iнтерполяцiйною формулою Лагранжа.

В точках значення многочлена i функцiї збігаються. При iнших значеннях рiзниця в загальному випадку вiдмiнна вiд нуля i є iстинною похибкою методу.

називається залишковим членом iнтерполяцiї.

Якщо функцiя в промiжку має неперервнi похiднi до -го порядку, то залишковий член можна подати в виглядi

(3)

де

(4)

--- залежить вiд i лежить усерединi вiдрiзка .

Позначивши через

(5)

одержимо таку оцiнку для абсолютної похибки iнтерполяцiйної формули Лагранжа:

(6)

Приклад 2.1. Знайти наближене значення функцiї в точцi за даними таблицi 2.1 за допомогою iнтерполяцiйної формули Лагранжа.

Табл. 2.1
	-0,6	-0,1	0,4
	2,18	2,38	2,55

Розв'язування.Iнтерполяцiйна формула Лагранжа має вигляд

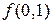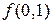Порiвняємо знайдене наближене значення з точним, знаючи, що таблицею задана функцiя . Точне значення дорiвнює

Отже, абсолютна похибка наближення дорiвнює

Таким чином, знайдено наближене значення функціїї з похибкою

Iнтерполяцiя сплайнами

На практицi ми можемо впливати вибором вузлiв на величину i не можемо впливати на властивостi функцiї, якi пов'язанi з її похiдними. Якщо з ростом величина зростає дуже швидко, то зростання степеня iнтерполяцiйного полiнома може привести до погiршення наближення функцiї. Iз ростом степеня при обчисленнях полiнома вiдбувається також швидке накопичування похибок округлення. Наприклад, при обчисленнях полiнома 100-го степеня в точцi старшi члени будуть машинними нулями. Тому на практицi полiноми вище 5-го степеня, як правило, не використовуються. Розбиття заданого вiдрiзка на кiлька частин разом iз побудовою на будь-якiй частинi свого iнтерполяцiйного многочлена незручне тим, що на стиках буде терпiти розрив перша похiдна двох сусiднiх iнтерполяцiйних полiномiв. Тому на практицi, щоб досить добре наблизити функцiю, замiсть iнтерполяцiйних полiномiв високих степенiв використовують iнтерполяцiйнi сплайни невисоких степенiв.

Слово "сплайн" походить вiд англiйського spline (рейка, стержень) --- назва пристосування, яке креслярi використовували для проведення гладких кривих через заданi точки. На практицi широко вживаються сплайни третього степеня, якi мають неперервну першу або першу і другу похiдну.