Глава 8. Кристаллическое состояние

Отличительные черты кристаллического состояния

Подавляющее большинство твердых тел в природе имеет кристаллическое строение. Характерная черта кристаллического состояния, отличающее его от жидкого и газообразного состояний, заключается в наличии анизотропии, т.е. зависимости ряда физических свойств (механических, тепловых, оптических, электрических) от направления. Причиной анизотропии кристаллов является упорядоченное расположение частиц (атомов, молекул), из которых они построены. Упорядоченное расположение частиц проявляется в правильной внешней огранке кристаллов. Кристаллы ограничены плоскими гранями, пересекающимися под некоторыми углами. Правильность геометрической формы и анизотропия кристаллов обычно не проявляются по той причине, что кристаллические тела встречаются, как правило, в виде поликристаллов, т.е. конгломератов множества сросшихся между собой беспорядочно ориентированных мелких кристалликов. В поликристаллах анизотропия наблюдается только в пределах каждого отдельно взятого кристаллика, тело же вследствие беспорядочной ориентации кристалликов анизотропии не обнаруживает.

Упорядоченность расположения атомов кристалла заключается в том, что атомы размещаются в узлах геометрически правильной пространственной решетки. Весь кристалл может быть получен путем многократного повторения в трех различных направлениях одного и того же структурного элемента, называемого элементарной кристаллической ячейкой (рис.1).

Длины ребер кристаллической ячейки называются периодами идентичности кристалла. Кристаллическая ячейка представляет собой параллелепипед, построенный на трех векторах 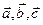, модули которых равны периодам идентичности. Этот параллелепипед, кроме ребер характеризуется так же углами и 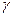между ребрами. Величины 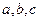и и 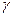однозначно определяют элементарную ячейку и называются ее параметрами. Элементарную ячейку можно выбрать различными способами. Кристаллическая ячейка, включающая наименьшее число атомов, характеризующих химический состав кристаллического вещества (например, один атом кислорода и два атома водорода для кристаллов льда) называется примитивной ячейкой. Однако обычно вместо примитивной выбирают элементарную ячейку с большим числом атомов, но обладающую такой же симметрией, как и весь кристалл в целом.

Классификация кристаллов

Кристаллическая решетка может обладать различными видами симметрии. Под симметрией кристаллической решетки понимается свойство решетки

совпадать с самой собой при некоторых пространственных перемещениях. Всякая решетка, прежде всего, обладает трансляционной симметрией, т.е. совпадает сама собой при перемещении (трансляции) на величину периода идентичности. Из других видов симметрии отметим симметрию по отношению к поворотам вокруг некоторых осей, а также к зеркальному отражению относительно определенных плоскостей. Если решетка совпадает само собой при повороте вокруг некоторой оси на угол , т.е. за один поворот вокруг оси решетка совпадает сама с собой 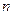раз, то эта ось называется осью симметрии 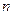-го порядка. Примеры структур, обладающих такими осями симметрии, показаны на рисунке 2 (белыми кружками, черными кружками и крестиками обозначены атомы разных сортов).

Плоскости, при зеркальном отражении от которых решетка совпадает само с собой, называется плоскостями симметрии.

Различные виды симметрии называются элементами симметрии кристаллической решетки.

Кристаллическая решетка, как правило, обладает одновременно несколькими видами симметрии. Однако не всякое сочетание элементов симметрии оказывается возможным. Как показал выдающийся русский ученый Е.С.Федоров, возможны 230 комбинаций элементов, получивших название пространственных групп. Эти 230 пространственные группы разбиваются по признакам симметрии на 32 класса. Наконец, по форме элементарной ячейки все кристаллы делятся на семь кристаллографических систем (или сингоний), каждая из которых включает в себя несколько классов симметрии. В порядке возрастающей симметрии кристаллографические системы располагаются следующим образом:

1. Триклинная система. Для нее характерно, что 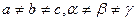. Элементарная ячейка имеет форму косоугольного параллелепипеда.

2. Моноклинная система. Два угла - прямые, третий (в качестве которого принято выбирать угол 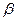), отличен от нуля. Элементарная ячейка имеет форму прямой призмы, в основании которой лежит параллелограмм (т.е. форму прямого параллелепипеда).

3. Ромбическая система. Все углы прямые, все ребра разные: 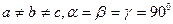. Элементарная ячейка имеет форму прямоугольного параллелепипеда.

4. Тетрогональная система. Все углы прямые, два ребра одинаковые: . Элементарная ячейка имеет форму прямой призмы с квадратным основанием.

5. Ромбоэдрическая (или тригональная) система. Все ребра одинаковые, все углы также одинаковые и отличные от прямого . Элементарная ячейка имеет форму куба, деформированного сжатием или растяжением вдоль диагонали.

6. Гексогональная система. Ребра и углы между ними удовлетворяют условиям: .

7. Кубическая система. Все ребра одинаковые, все углы прямые 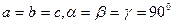. Элементарная ячейка имеет форму куба.