Оцениваем прочность стержня

Сопоставляем наибольшее (по модулю) нормальное напряжение 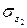, которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением 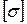. Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения 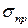, то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: 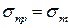. Тогда

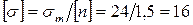кН/см2.

Условие прочности имеет вид 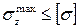. В нашем случае

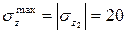кН/см2 > 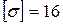кН/см2,

следовательно, прочность стержня на втором участке не обеспечена.

Таким образом, площадь поперечного сечения стержня на втором участке, равную 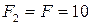см2, нам необходимо увеличить.

Несложный анализ показывает, что на других участках стержня условие прочности выполняется.

Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:

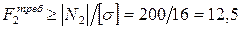см2.

Принимаем на втором участке 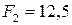см2.

Вычисляем удлинение всего стержня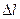

При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле

,

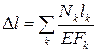где E – модуль Юнга, а 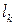– длина соответствующего участка стержня.

Тогда

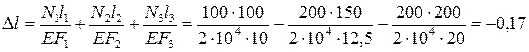см.

Таким образом, длина стержня уменьшается на 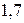мм.

ЗАДАЧА ПО СОПРОМАТУ НА РАСТЯЖЕНИЕ И СЖАТИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Условие задачи на растяжение и сжатие

Стальной стержень (модуль Юнга 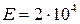кН/см2) находится под действием внешних осевых сил 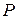и 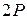(рис. 3.1). Построить эпюры продольных сил 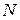и нормальных напряжений 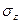. Оценить прочность стержня, если предельное напряжение (предел текучести) 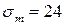кН/см2, а допускаемый коэффициент запаса 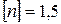. Найти удлинение стержня .

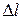СХЕМЫ ДЛЯ ЗАДАЧИ НА РАСТЯЖЕНИЕ И СЖАТИЕ

Исходные данные к задаче на растяжение и сжатие

Номер схемы	F, см2	a, м	b, м	c, м	P, кН
	2,0	1,2	1,4	1,6
	2,2	1,4	1,6	1,4
	2,4	1,8	1,6	1,2
	2,6	1,6	2,0	1,0
	2,8	2,0	1,8	1,2
	3,0	2,2	1,6	1,4
	3,2	2,4	1,4	1,6
	3,4	2,6	1,2	1,8
	3,6	2,8	1,0	1,4
	3,8	2,4	1,6	1,2

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ НА КРУЧЕНИЕ СТЕРЖНЯ КРУГЛОГО СЕЧЕНИЯ

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ "ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ" №1

Условие примера задачи на прямой поперечный изгиб

Для консольной балки, нагруженной распределенной нагрузкой интенсивностью 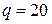кН/м и сосредоточенным моментом 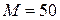кН·м (рис. 3.12), требуется: построить эпюры перерезывающих сил и изгибающих моментов 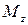, подобрать балку круглого поперечного сечения при допускаемом нормальном напряжении 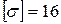кН/см2 и проверить прочность балки по касательным напряжениям при допускаемом касательном напряжении 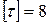кН/см2. 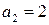Размеры балки м; 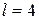м; м.

Расчетная схема для задачи на прямой поперечный изгиб

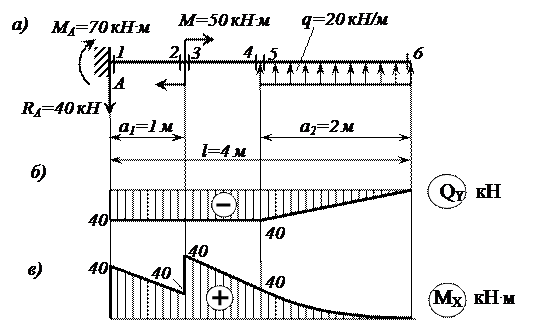Рис. 3.12

Решение задачи "прямой поперечный изгиб"