Пример. Получилась функция, аналитическая в полосе (мероморфная во всей плоскости, с полюсами на границах полосы)
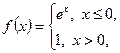
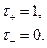
Получилась функция, аналитическая в полосе 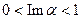 (мероморфная во всей плоскости, с полюсами на границах полосы). Отметим, что первый интеграл сходится только при
(мероморфная во всей плоскости, с полюсами на границах полосы). Отметим, что первый интеграл сходится только при 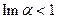 , а второй – при
, а второй – при 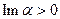 .
.
Обращением предыдущей теоремы является следующая
Теорема [6].Пусть функция 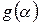 ,
, 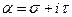 , голоморфна в полосе
, голоморфна в полосе 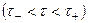 и пусть
и пусть 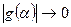 равномерно, когда
равномерно, когда 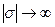 в полосе
в полосе 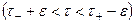 , где
, где 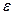 – произвольное положительное число. Тогда для функции
– произвольное положительное число. Тогда для функции
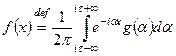 ,
,
где 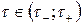 , а
, а 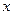 – вещественно, имеет место соотношение
– вещественно, имеет место соотношение
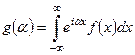 .
.
Кроме того, 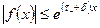 при
при 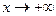 и
и 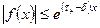 при
при 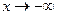 , где
, где 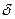 –произвольное, сколь угодно малое положительное число.
–произвольное, сколь угодно малое положительное число.
Функцию 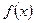 , определенную в утверждении теоремы можно считать решением интегрального уравнения
, определенную в утверждении теоремы можно считать решением интегрального уравнения
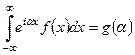 .
.
Доказательство.Проверим непосредственно последнее равенство:
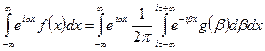 .
.
Пусть 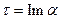 в этом равенстве. Выберем
в этом равенстве. Выберем 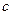 и
и 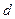 так, что
так, что 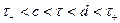 и перейдем во внутреннем интеграле на параллельную прямую
и перейдем во внутреннем интеграле на параллельную прямую 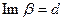 для
для 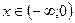 , а для
, а для 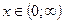 – на прямую
– на прямую 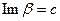 :
:
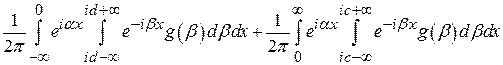 .
.
Сдвиги сделаны для того, чтобы можно было поменять порядок интегрирования. До сдвигов мы имели 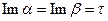 , а после сдвигов в первом интеграле
, а после сдвигов в первом интеграле 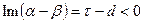 и
и 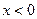 , а во втором
, а во втором 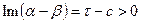 и
и 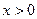 . Эти неравенства гарантируют экспоненциальное убывание модуля подынтегральной функции при
. Эти неравенства гарантируют экспоненциальное убывание модуля подынтегральной функции при  (с учетом
(с учетом 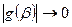 при
при 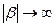 ). Отметим здесь, что абсолютная сходимость полученных повторных интегралов влечет в силу теоремы Фубини сходимость при почти всех
). Отметим здесь, что абсолютная сходимость полученных повторных интегралов влечет в силу теоремы Фубини сходимость при почти всех 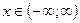 и независимость от
и независимость от 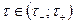 интеграла, определяющего функцию f(x).
интеграла, определяющего функцию f(x).
После перемены порядка интегрирования и вычисления внутренних интегралов будем иметь
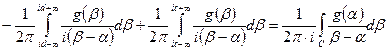 , где
, где 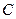 – замкнутый контур, получающийся в пределе из прямоугольника
– замкнутый контур, получающийся в пределе из прямоугольника 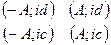 при
при 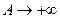 , причем этот прямоугольник обходится в положительном направлении (против часовой стрелки). Так как по условию
, причем этот прямоугольник обходится в положительном направлении (против часовой стрелки). Так как по условию 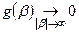 равномерно в полосе
равномерно в полосе 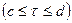 , то интегралы по вертикальным сторонам прямоугольника в пределе обращаются в нуль.
, то интегралы по вертикальным сторонам прямоугольника в пределе обращаются в нуль.
По теореме Коши о вычетах (интегральная формула Коши) имеем 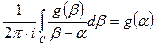 .
.
Далее, если 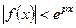 при
при 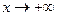 и
и 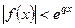 при
при 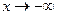 , то из формулы
, то из формулы 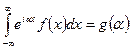 следует, что
следует, что 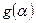 голоморфна в полосе
голоморфна в полосе 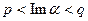 . Однако, по условию
. Однако, по условию 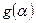 голоморфна при
голоморфна при 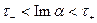 . Следовательно, можно положить
. Следовательно, можно положить 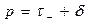 ,
, 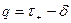 , где
, где 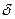 – произвольно малое положительное число.
– произвольно малое положительное число.
Теорема доказана.
