Построение эпюр поперечных, продольных сил и изгибающих моментов
В нашем примере рама имеет четыре участка, как показано на рис.16.Выражения для внутренних усилий и их эпюры определяются для каждого участка рамы в отдельности. Для горизонтальных участков остаются верны те же знаки внутренних силовых факторов, что и для балок, а вертикальные участки сводим к горизонтальным поворотом рамы по ходу часовой стрелке.
Проводим сечение на I участке (рис.16). Поскольку участок занимает вертикальное положение, развернем раму по ходу часовой стрелке и рассмотрим левую от сечения часть.
 I участок
I участок 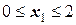 (начало отсчета на левом конце);
(начало отсчета на левом конце);
Q(x1) = HB – q1 x1= 3,33кН– 3кН/м·x1;
Q(0) = 3,33кН– 3кН/м·0= 3,33кН (значение на левой границе участка);
Q(2м) = 3,33кН– 3кН/м·2м = – 2,67кН (значение на правой границе участка);
Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:
Q(x0) = 3,33кН – 3кН/м·x0=0; x0= 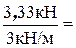 1,11м.
1,11м.
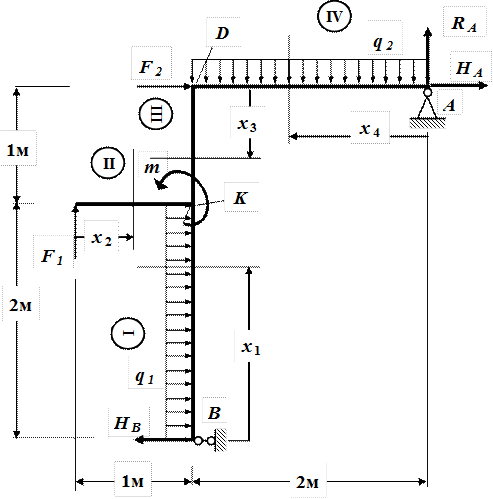
Рис.16.
Изгибающий момент на этом участке
 M(x1) = HBx1 –
M(x1) = HBx1 – 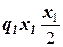 = 3,33кН ·x1– 3
= 3,33кН ·x1– 3 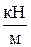 ·
· 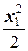 = 3,33кН ·x1– 1,5кН/м·
= 3,33кН ·x1– 1,5кН/м· 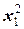 ;
;
Слева от сечения моменты всех сил берем относительно центра тяжести поперечного сечения (рис.16).
Изгибающий момент (M) является квадратичной функцией координаты x1.
Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке.
M (0) = 3,33кН ·0– 1,5кН/м· 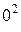 =0 (значение на левой границе участка);
=0 (значение на левой границе участка);
M (1,11м) = 3,33кН ·1,11м– 1,5кН/м·(1,11м )2 = 1,84815кНм=1,85 кНм;
M (2м) = 3,33кН·2м– 1,5кН/м·(2м)2 = 0,66кНм (значение на правой границе уч-ка).
N(x1) =0 (слева от сечения отсутствуют силы, действующие параллельно оси участка).
Проводим сечение на II участке и рассматриваем левую от сечения часть рамы (рис.16).
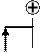 II участок
II участок 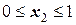 (начало отсчета на левой границе участка).
(начало отсчета на левой границе участка).
Q(x2) = F1= 6кН;
 |
M (x2) = F1 x1 = 6кН ·x1;
M (0) = 6кНм·0 = 0 (значение на левой границе участка);
M (1м) = 6кН·1м= 6 кНм (значение на правой границе участка).
N (x2) =0 (слева от сечения отсутствуют силы, действующие параллельно оси участка).
Проводим сечение на III участке. Поскольку участок занимает вертикальное положение, развернем раму по ходу часовой стрелке. Будем рассматривать правую от сечения часть рамы (частьIII-го участка иIV участок).
III участок 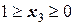 (начало отсчета на правой границе участка);
(начало отсчета на правой границе участка);
 |
 Q(x3) = F2 +HA =5кН – 7,67кН= –2,67кН.
Q(x3) = F2 +HA =5кН – 7,67кН= –2,67кН.
M (x3) = – F2 x3 – Rq2 · 1м + RA·2м – HA · x3 =
= –5кН ·x3 – 8кН ·1м +2кН·2м –(–7,67кН)· x3 = 2,67кН· x3 – 4кНм.
M (0) = 2,67кН ·0– 4кНм = – 4кНм (значение на правой границе участка);
M (1м) = 2,67кН ·1м– 4кНм = – 1,33кНм (значение на левой границе участка).
 N(x3) = RA – Rq2 = 2кН– 8кН= – 6кН.
N(x3) = RA – Rq2 = 2кН– 8кН= – 6кН.
Продольная сила является постоянной, графиком такой функции служит прямая линия, параллельная оси участка.
Проводим сечение на IV участке. Будем рассматривать правую от сечения часть рамы (рис.16).
IV участок 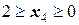 (начало отсчета на правой границе участка).
(начало отсчета на правой границе участка).
 |
Q(x4) = – RA + q2 x4= – 2кН + 4кН/м·x4;
Q(0) = – 2кН + 4кН/м·0= – 2кН;
Q(2м) = – 2кН + 4кН/м·2м = 6кН.
Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:
Q(x0) = – 2кН + 4кН/м ·x0=0; x0= 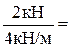 0,5м.
0,5м.
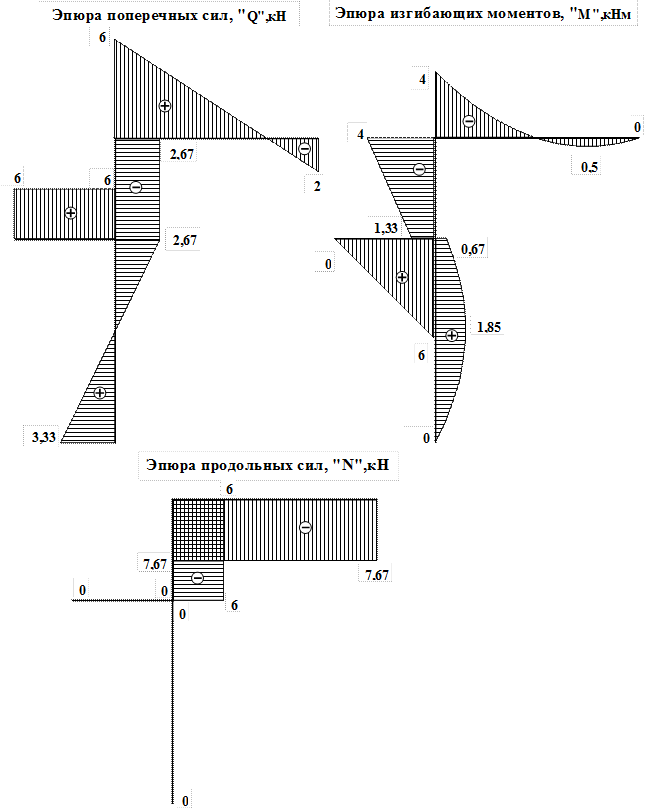
Рис.17
 Изгибающий момент на этом участке
Изгибающий момент на этом участке
M(x4) = RAx4 – 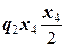 = 2кН·x4 – 4
= 2кН·x4 – 4 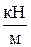 ·
· 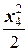 = 2кН ·x4– 2кН/м·
= 2кН ·x4– 2кН/м· 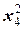 ;
;
Справа от сечения моменты всех сил берем относительно центра тяжести поперечного сечения (рис.16).
Изгибающий момент (M) является квадратичной функцией координаты x4.
Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке.
M (0) = 2кН ·0– 2кН/м·0=0 (значение на правой границе участка);
M (0,5м) = 2кН·0,5м– 2кН/м·(0,5м )2=0,5кНм;
M (2м) = 2кН·2м– 2кН/м·(2м )2 = –4кНм(значение на левой границе участка).
 N(x4) = HA = – 7,67кН.
N(x4) = HA = – 7,67кН.
Эпюры поперечных сил, изгибающих моментов и продольных сил показаны на рис.17.
Проверка равновесия узлов
Построенные эпюры поперечных сил и изгибающих моментов проверяются по правилам контроля и построения эпюр для прямолинейных балок. Кроме этого необходимо проверить равновесие узлов. Узлом в раме называется точка соединения вертикальных и горизонтальных участков. В нашем примере это узел D и узел K (рис. 16).
Положительные направления внутренних силовых факторов для узла в виде креста показаны на рис.18.
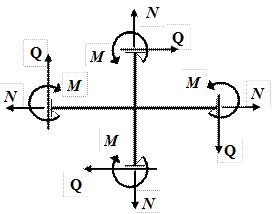 |
Рис. 18
Вырежем узел D и проверим его равновесие. В узле D сходятся IIIиIVучастки, приложена горизонтальная сила F2 = 5 кН (рис.19).
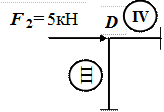
Рис.19
Используя рис.17, приведем фрагменты эпюр поперечных, продольных сил и изгибающих моментов в окрестности узла D(рис. 20).
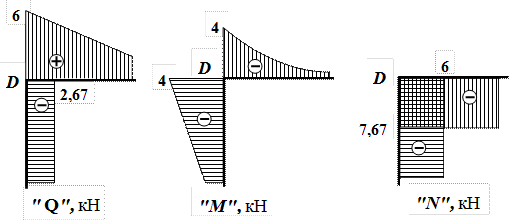 |
Рис.20
В узле D внутренние силовые факторы принимают следующие значения:
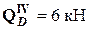 (при подходе к узлу справа);
(при подходе к узлу справа);
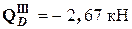 (при подходе к узлу снизу);
(при подходе к узлу снизу);
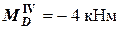 (при подходе к узлу справа);
(при подходе к узлу справа);
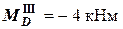 (при подходе к узлу снизу);
(при подходе к узлу снизу);
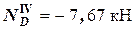 (при подходе к узлу справа);
(при подходе к узлу справа);
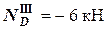 (при подходе к узлу снизу).
(при подходе к узлу снизу).
С учетом правила знаков (рис.18), показываем истинные направления внутренних усилий приложенных в окрестности узла D (рис.21).
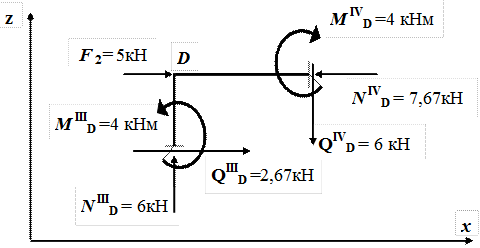 |
Рис.21
Составляем три уравнения статики:
S Fx =0: 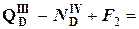 2, 67 кН –7,67кН +5 кН = 7, 67кН –7, 67кН=0;
2, 67 кН –7,67кН +5 кН = 7, 67кН –7, 67кН=0;
S Fz=0: 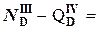 6 кН –6кН =0;
6 кН –6кН =0;
S MD =0: 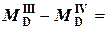 4 кНм –4кНм =0.
4 кНм –4кНм =0.
УзелD находится в равновесии.
Вырежем узел K и проверим его равновесие. В узле K сходятся I,IIи IIIучастки, приложен сосредоточенный момент m = 8 кНм (рис.22).
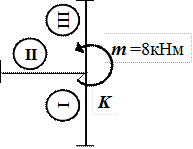 |
Рис.22
Используя рис.17, приведем фрагменты эпюр поперечных, продольных сил и изгибающих моментов в окрестности узла K (рис. 23).
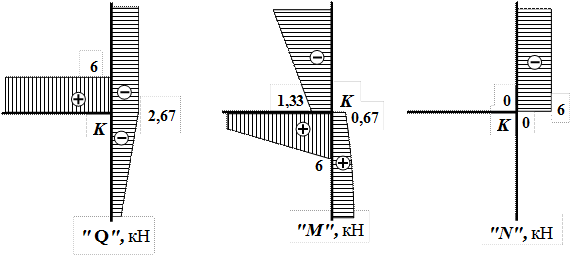 |
Рис. 23
В узле K внутренние силовые факторы принимают следующие значения:
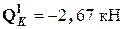 (при подходе к узлу снизу);
(при подходе к узлу снизу);
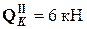 (при подходе к узлу слева);
(при подходе к узлу слева);
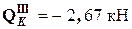 (при подходе к узлу сверху);
(при подходе к узлу сверху);
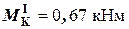 (при подходе к узлу снизу);
(при подходе к узлу снизу);
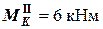 (при подходе к узлу слева);
(при подходе к узлу слева);
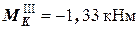 (при подходе к узлу сверху);
(при подходе к узлу сверху);
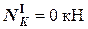 (при подходе к узлу снизу);
(при подходе к узлу снизу);
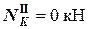 (при подходе к узлу слева);
(при подходе к узлу слева);
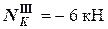 (при подходе к узлу сверху).
(при подходе к узлу сверху).
С учетом правила знаков (рис.18), показываем истинные направления внутренних усилий приложенных в окрестности узла K (рис.24).
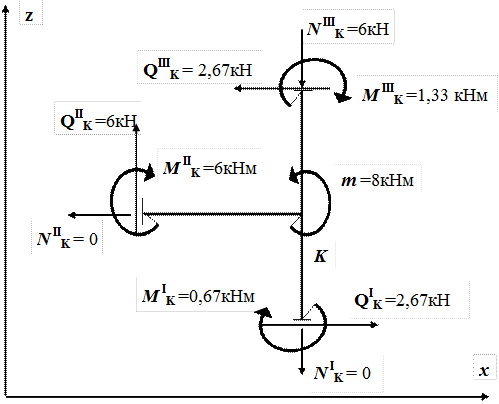
Рис.24
Составляем три уравнения статики:
S Fx =0: 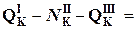 2, 67 кН – 0 – 2, 67кН=0;
2, 67 кН – 0 – 2, 67кН=0;
S Fz=0: 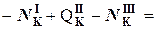 0+ 6 кН –6кН =0;
0+ 6 кН –6кН =0;
S MK=0: 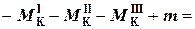 –0.67кНм –6кНм –1.33кНм +8кНм =
–0.67кНм –6кНм –1.33кНм +8кНм =
= –8кНм +8кНм =0.
УзелK находится в равновесии.
Эпюры продольных сил, поперечных сил и изгибающих моментов построены правильно.
