Закон био − савара − лапласа
Согласно закону Био − Савара − Лапласа элемент проводника dl с током I создает в некоторой точке А индукцию поля, равную:
| I | |||||||||
| dB =μμ | dl | ×r | , | (1.2.1) | |||||
| 4πr3 | |||||||||
| где r − радиус-вектор, проведенный из элемента dl проводника в точ- | |||||||||
| ку А. Направление dB | перпендикулярно dl | и r | и совпадает с каса- | ||||||
| тельной к линии магнитной индукции (рис.1.2.1). | |||||||||
| dl | |||||||||
| r | |||||||||
| I | dB |
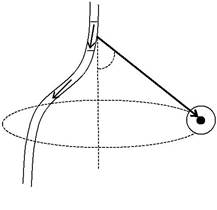
Рис. 1.2.1
| Модуль вектора dB определяется выражением | |||||||||||
| dB =μμ | I | dl sinα, | (1.2.2) | ||||||||
| 0 4πr2 | |||||||||||
| где α − угол между векторами dl | и r. | ||||||||||
| Для напряженности магнитного поля закона Био − Савара − Лап- | |||||||||||
| ласа будет иметь вид: | |||||||||||
| I | I | ||||||||||
| dH | = | dl ×r | и dH = | dl sinα. | (1.2.3) | ||||||
| 4 πr3 | 4πr2 | ||||||||||
Закон Био − Савара − Лапласа совместно с принципом суперпози-ции магнитных полей позволяет найти индукцию магнитного поля, создаваемого проводником любой конфигурации. В этом случае прин-
| цип суперпозиции магнитных полей будет иметь вид | |
| B =∫dB или H =∫dH. | (1.2.4) |
Расчет магнитных полей прямого проводника с током бесконечной и конечной длины.
Пусть прямолинейный проводник MN конечной длины с током I лежит в плоскости чертежа (рис. 1.3.1). Согласно закону Био – Сава-
ра – Лапласа (1.2.2), вектор магнитной индукции dB перпендикулярен плоскости чертежа и направлен «к нам». Численное значение индук-ции магнитного поля dB, создаваемого в точке А элементом dl про-водника с током I равно:
| dB = μμ0 Idl sinα , | (1.3.1) | |||
| 4πr2 | ||||
| где ϕ – угол между векторами dl | и r. | |||
| M | ||||
| αD1 | dα | |||
| dl C | α | r | ||
| I | r0 | B | ||
| N | α2 | |||
| Рис. 1.3.1 |
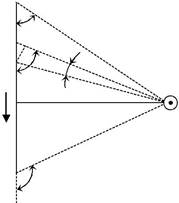
Вектора dB от каждого элемента dl имеют одинаковое направ-
| ление, так как проводник прямолинейный, | и поэтому суммарная маг- | |||||
| нитная индукция равна | ||||||
| B =∫ dB = | μμ 0 I | ∫dl sin2 | α. | (1.3.2) | ||
| 4π | l | r |
Преобразуем выражение (1.3.2) таким образом, чтобы магнитная ин-дукция стала функцией одной переменной α. Из рис. 1.3.1 следует, что
r =sinr0ϕ,а dl =sinCDϕ=sinrdαϕ.



Тогда
dl =sinr0d2αα.

Подставив полученные значения r и dl получим:
B = μμ0 I α∫2 sin αd α,
4πr0 α1
в соотношение (1.3.2),
(1.3.3)
где α1 и α2 – значения угла α для крайних точек проводника MN. Проинтегрировав равенство (1.3.3), получим формулу для расчета
магнитной индукции прямого проводника с током конечной длины
| B = | μμ0 I (cos α1 − cos α2 ). | (1.3.4) |
| 4πr0 |
Если проводник MN бесконечно длинный, то α1 = 0, а α2 = π. То-гда из (1.3.4) магнитная индукция прямого проводника с током беско-нечной длины в любой точке поля вне проводника равна:
| B = | μμ0I | . | (1.3.5) | |
| 4πr | ||||
Напряженность магнитного поля вычисляется по формуле H = μμB0

и для прямолинейного проводника с током конечной длины равна:
| H = | I | (cos α − cos α | ), | (1.3.6) | |||||
| 4πr0 | |||||||||
| а для бесконечно длинного проводника: | |||||||||
| H = | I | . | (1.3.7) | ||||||
| 4πr | |||||||||
Лекция № 2
1.4. Магнитное поле движущейся заряженной частицы.
1.5. Циркуляция вектора магнитной индукции.
1.6. Магнитное поле тороида и соленоида.
1.7. Магнитный поток. Теорема Гаусса для магнитного поля в ин-тегральной и дифференциальной формах.
