Алгебраический момент силы относительно точки

Введение

Современная механика – это отрасль знаний, которая поставляет и исследует механические модели для описания изменений положения и формы материальных объектов.

Теоретическая механика – это раздел общей механики, в которой развиваются математические методы исследования механического движения и механического взаимодействия материальных точек, механических систем и абсолютно твердых тел. Теоретическая механика как наука о движении представляет собой научную базу многих отраслей современной техники и машиностроения. Теоретическая механика содержит разделы, которые называются статика, кинематика, динамика и аналитическая механика.

Статика – раздел теоретической механики, в котором рассматривают свойства сил, приложенных к точкам твердого тела, и условия их равновесия.

В кинематике изучают чисто геометрические формы механических движений материальных объектов без учета условий и причин, вызывающих и изменяющих эти движения.

В динамике изучаются механические движения материальных объектов в зависимости от сил, т.е. от действия на рассматриваемые объекты других материальных объектов.

В аналитической механике изучаются равновесие и движение механических систем в терминах возможного перемещения точки и системы при применении обобщенных координат и обобщенных сил.

Целью преподавания теоретической механики студентам технических специальностей, является обеспечение их знаниями, необходимыми для решения вопросов механики в производственно-технологических проектах, конструкторских и исследовательских задачах.

Для изучения курса необходимо иметь соответствующую математическую подготовку. Перечень разделов других дисциплин, знание которых необходимо при изучении теоретической механики:

– Дисциплина «Математика». Разделы:

«Векторная алгебра» (операции над векторами, скалярное, векторное и смешанное произведение; определители, матрицы, методы решения алгебраических систем);

«Дифференциальное и интегральное исчисление» (понятие дифференциала и производной; вычисление и геометрический смысл производных; производные сложных функций; функции многих переменных, частные производные; неопределенный интеграл; криволинейные, двойные, тройные интегралы, примеры вычисления площадей и объемов, центров тяжести фигур);

«Дифференциальные уравнения» (обыкновенные дифференциальные уравнения первого и второго порядков, общие и частные решения; примеры интегрирования дифференциальных уравнений, методы разделения переменных, вариации переменных и др.; однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, подстановки Эйлера, приемы отыскания частных решений);

«Элементы вариационного исчисления» (понятие функционала и вариации, принцип наименьшего действия).

– Дисциплина «Физика». Разделы:

«Физические основы классической механики» (элементы кинематики точки; динамика материальной точки; законы сохранения; потенциальная и кинетическая энергии системы; осевые моменты инерции твердого тела; элементы кинематики твердого тела);

«Колебания и волны» (гармонические колебания и их характеристики; дифференциальные уравнения гармонических колебаний).

В результате изучения данной дисциплины студенты должны иметь представление о свойствах механического движения объектов в пространстве с течением времени, знать и уметь использовать методы, понятия, модели и законы теоретической механики, иметь навыки исследования механического взаимодействия материальных объектов.

При изучении материала сначала следует прочитать весь материал темы, особенно не задерживаясь на том, что представляется не совсем понятным. Часто первоначально не ясные положения становятся понятны при дальнейшем изложении материала. Затем следует вернуться к местам, вызвавшим затруднения и внимательно разобраться в том, что было неясно. Особое внимание при повторном чтении следует обратить на формулировки основных понятий, определений, теорем и т.п. В точных формулировках существенно каждое слово и очень полезно понять, почему данное положение сформулировано именно так.

Закончив изучение темы, полезно составить краткий конспект. При составлении конспекта следует указывать страницы учебника, на которых излагается соответствующий раздел, и заносить возникающие вопросы. При составлении конспекта следует использовать и материалы обзорной лекции, приводимой на установочных занятиях.

Статика

Основные понятия статики

В статике твердого тела рассматриваются свойства сил, приложенных к твердому телу. В частности, изучается приведение сложных систем сил к более простому виду и устанавливаются условия равновесия различных систем сил, действующих на твердое тело или материальную точку.

Материальная точка – простейшая модель материального тела любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу.

Механической системой называется любая совокупность материальных точек, положение и движение которых между собой связаны.

Абсолютно твердым телом (или неизменяемой механической системой) называют механическую систему, расстояния между точками которой не изменяются при любых взаимодействиях.

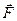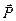Силой называют одну из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила кроме числового значения характеризуется точкой приложения и направлением действия. Она является векторной величиной. Силу как величину векторную обозначают какой-либо буквой со знаком вектора, например или . Для выражения числового значения силы или ее модуля используется знак модуля от вектора, т.е. 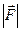, 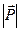или те же буквы, но без знака вектора, т. е. , .

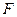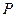Системой сил называют совокупность сил, действующих на рассматриваемый материальный объект.

Системой сил, эквивалентной нулю (или равновесной системой сил), называют такую систему сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.

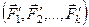Две системы сил и называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях. Условие эквивалентности двух систем сил и 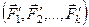выражают в форме:

~ ,

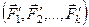где 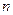и 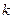– число сил в системах.

Равнодействующей силой рассматриваемой системы сил называют силу, действие которой на твердое тело или материальную точку эквивалентно действию этой системы сил. Равнодействующая сила обозначается 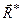, условие ее эквивалентности рассматриваемой системе сил выражается в виде:

~ .

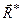Отметим, что не каждая система сил имеет равнодействующую

Уравновешивающей силой заданной системы сил считается такая сила, добавление которой к заданной дает новую систему, эквивалентную нулю. Если 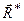является уравновешивающей силой системы сил 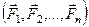, то, согласно определению, она удовлетворяет условию:

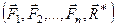~0.

Момент силы

Алгебраический момент силы относительно точки

Алгебраическим моментом силы 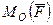относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис. 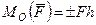1).

. (1)

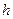Плечом силы 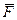относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т.е. длину отрезка перпендикуляра, опущенного из точки 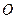на линию действия силы .

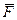Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке – знак минус.

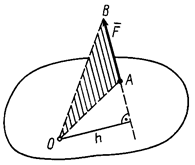Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю.