К кому подойти на вечеринке?
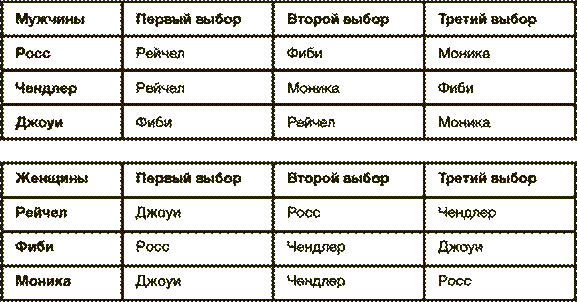
Представим себе компанию из трех молодых людей и трех девушек, весело болтающих в клубе. Назовем их Джоуи, Чендлер, Росс, Фиби, Моника и Рейчел. Предположим, что у каждого из этих юношей и девушек есть определенные предпочтения, ранжированный список тех, с кем им хотелось бы завести роман.
Несмотря на то, что все персонажи и события в этом случае полностью вымышлены и никак не связаны ни с одним из тщательно охраняемых авторским правом сериалов, я решила – опятьтаки, совершенно случайно – сделать Монику и Росса братом и сестрой. Но я также решила, что они скорее покинут вечеринку вместе (оставшись в платонических отношениях, разумеется), чем в одиночку, так что они все равно являются друг для друга выбором третьей очереди.
Самая популярная девушка – Рейчел, она стоит на первом месте и в списке Росса, и в списке Чендлера. В то же время и Рейчел, и Моника в своих рейтингах на первое место поставили Джоуи.

Налицо конфликт интересов, и если никто не хочет уйти с вечеринки без пары, необходим какой-то компромисс.
Если этот сценарий будет разыгрываться по весьма старомодному правилу “кавалеры приглашают дам”, то каждый из молодых людей попытается приударить за своей девушкой из первой очереди выбора.
Поскольку за Рейчел будут ухаживать одновременно Росс и Чендлер, ей придется выбирать между ними. В ее списке Росс стоит выше, чем Чендлер, так что будем считать, что Рейчел и Росс образовали пару – во всяком случае, пока (ведь Рейчел все еще втайне надеется, что на нее обратит внимание Джоуи).
Чендлер, оставшийся без партнерши и продолжающий поиск, обратится к своей девушке “второго выбора” – Монике. Поскольку у Моники нет других вариантов, она примет ухаживания Чендлера, хотя, как и Рейчел, предпочла бы Джоуи.
Фиби, не получив предложений ни от Росса, ни от Чендлера, остается с Джоуи.
Итак, теперь все утряслось, у всех парней есть пары:
1. Росс – Рейчел.
2. Чендлер – Моника.
3. Джоуи – Фиби.
Создалась ситуация, которую, с точки зрения парней, уже нельзя улучшить. Лишь Чендлер остался без своего выбора первой очереди – Рейчел, но она сама его отвергла. У парней нет причин меняться партнершами, даже если кто-то из девушек вдруг решит сделать еще одну попытку остаться с парнем, который ей нравится в первую очередь. Конечно, Рейчел предпочла бы Джоуи, но тот ведь уже получил свой предпочтительный выбор и совершенно не заинтересован в обмене.
С точки зрения девушек распределение выглядит не столь удачным. Рейчел, Фиби и Монике достался в конце концов их, соответственно, второй, третий и второй выбор. Не очень-то высокий результат для списка из трех человек, особенно по сравнению с парнями, которые заполучили первый, второй и первый номера из своих списков.
Вся эта история иллюстрирует математическую “задачу стабильного брака” (она же “задача о марьяже”), а подобный процесс поиска партнеров получил название алгоритма Гейла – Шепли, или “алгоритма отложенного согласия”. Если мы более внимательно присмотримся к математической стороне ситуации, то увидим нечто поразительное. Независимо от того, сколько парней и девушек принимают участие в процессе, выходит так, что всякий раз, когда парни делают первый шаг, возможны следующие четыре результата:
1. Каждый находит себе партнера.
2. После того, как все пары определились, ни один парень из какой-либо пары и ни одна девушка из другой пары не смогли бы оба стать более счастливыми, если бы попытались соединиться (да, Фиби, возможно, по-прежнему неравнодушна к Россу, но он-то ведь счастлив с Рейчел).
3. После того как определились все пары, каждый парень получает лучшую из доступных для него девушек.
4. После того, как определились все пары, каждая девушка оказывается с “наименее плохим” из всех парней, которые пытались за ней ухаживать.
Последние два пункта самые удивительные: коротко говоря, группа, которая делает первый шаг (пусть ее участники и рискуют тем, что нарвутся на отказ), в конечном счете все равно оказывается в выигрыше по сравнению с группой, которая вела себя пассивно (то есть только принимала или отклоняла ухаживания).
Мы можем повторить этот простой эксперимент, поменяв ролями женщин и мужчин. Если первый шаг сделают девушки, то, используя те же расчеты, мы получим такие пары:
1. Рейчел – Джоуи.
2. Фиби – Росс.
3. Моника – Чендлер.
Теперь каждая из девушек получила соответственно свой первый, первый и второй выбор – это явное улучшение. В то же время у молодых людей оказались соответственно три вторых выбора – гораздо более низкий результат по сравнению с первым вариантом, когда они играли активную роль.
Этот результат интуитивно понятен. Если вы проявите инициативу и пойдете по своему списку сверху вниз, то в любом случае вам достанется лучшая из возможных в данной ситуации кандидатур. Если же будете сидеть и ждать, пока кто-то подойдет к вам, то в результате окажетесь с “наименее плохим” партнером из всех, кто проявит интерес к вам. Независимо от того, насколько серьезных отношений вы ищете, всегда стоит проявлять инициативу.
Разница в результатах для тех, кто проявляет инициативу и для тех, кто ждет, особенно важна в тех случаях, когда “задача о марьяже” применяется для решения проблем, выходящих за рамки поиска партнера на вечеринке. Например, начиная с 1950-х годов правительство США использует алгоритм Гейла – Шепли в Национальной программе подбора ординатуры (NRMP ), цель которой – оптимальное распределение молодых врачей по больницам. В свое время “предложение” выпускникам ординатуры первыми делали больницы. Это давало им возможность заполучить именно тех молодых медиков, которые были им нужны, но не очень подходило самим врачам, которым иногда приходилось переезжать на другой конец страны, чтобы принять “лучшее из худших” предложение. В результате множество врачей были не вполне удовлетворены своим местом работы, а это, в свою очередь, было плохо для больниц и для всей системы здравоохранения. Когда это стало очевидным, организаторы программы предложили врачам взять инициативу в свои руки и самим “делать предложение” той или иной больнице.
Однако и больницами дело тоже не ограничивается. Алгоритм поиска партнеров Гейла – Шепли используется во множестве сценариев реальной жизни: последипломная подготовка стоматологов, трудоустройство юристов в Канаде, набор учеников в выпускные классы и студенческие братства. Этот алгоритм настолько полезен, что существует масса научной литературы, посвященной исследованию пределов его применимости и особых случаев применения – и многие из этих особых случаев как раз относятся к сфере знакомств и установления отношений.
Математики усовершенствовали метод таким образом, чтобы в качестве инициаторов отношений (причем как по отношению к противоположному, так и к своему полу) могли одновременно выступать и мужчины, и женщины, а также изменили правила, включив в рейтинги предпочтений взаимные связи. Кроме того, они предусмотрели сценарий, согласно которому вы предпочтете уйти с вечеринки в одиночестве, чем подойти вон к тому странному типу, что сидит в углу. Ученые даже исследовали, что именно происходит, когда вы обманываете мужчин (но, как ни странно, не предусмотрели сценария, в котором вы обманываете женщин).
В этих особых случаях математика ситуации может быть уже достаточно сложной (хотя, если вам интересно, в конце книги приведено некоторое количество весьма любопытных ссылок). Но при всех натяжках и исключениях вывод остается одним и тем же: если вы в состоянии время от времени выслушивать обидные отказы, ваша предприимчивость в конечном счете будет вознаграждена. Всегда лучше сделать первый шаг, чем сидеть и ждать, пока кто-нибудь подойдет к вам. Поэтому задавайте себе высокую планку и делайте это почаще. Так говорит математика.
Знакомства в интернете
Итак, будем надеяться, что вы достаточно отважны, чтобы подойти к самому яркому персонажу вечеринки, вооружившись самыми общими знаниями “задачи о марьяже”. Но слишком много вечеринок подряд – это изнурительно, вы не находите? К тому же не факт, что на них всегда будут присутствовать столь привлекательные герои, как Джоуи и Рейчел. В таком случае почему бы не испробовать способ, с которым вы можете добиться успеха, не покидая собственной квартиры? Настало время для знакомства в интернете!
Сегодня, наверное, у каждого из нас есть знакомые пары, нашедшие друг друга в Сети. И, несмотря на все предрассудки и стереотипы, мы с энтузиазмом восприняли этот новый подход к поиску любви. Последние данные статистики свидетельствуют, что в США три четверти одиноких людей прибегали к помощи сайтов знакомств и до трети молодых супругов нашли друг друга через интернет.
Привлекательность метода очевидна. Не нужно набираться храбрости, чтобы знакомиться с девушкой в баре на глазах своих друзей и ее подруг, или рисковать тем, что придется убить вечер в компании какого-нибудь очаровательного овоща. В морях интернета водится гораздо больше рыбы. Современные сайты знакомств предлагают бесчисленное множество кандидатур, как будто специально подобранных под ваши запросы, и кажется, что от встречи с идеалом вас отделяет лишь одно нажатие клавиши.
Во всяком случае, мы думаем, что так должно быть, но иногда, когда выбор чересчур большой, бывает трудно отсечь сомнительные варианты. Для некоторых из нас попытки познакомиться онлайн превращаются в череду встречи с лягушками, не имеющими ни малейшего шанса превратиться (по крайней мере, с нашей точки зрения) в принца или принцессу. Кроме того, больше возможностей – больше отказов. Как всегда, хорошая новость заключается в том, что на помощь нам может прийти математика.
Для математиков, которые, подобно мне, изучают закономерности человеческого поведения, сайты онлайн-знакомств – просто подарок судьбы, неисчерпаемый кладезь информации. Следы, которые люди оставляют в интернете, позволили получить огромное количество новых знаний о любви и новых взглядов на нее. Изучая ничего не подозревающих одиночек, математики вырабатывают новый, научный, подход к технике флирта. Анализируя отношения людей, которые нашли друг друга через сайты знакомств, мы также начинаем понимать, почему все существовавшие до настоящего времени системы “научного” знакомства плохо работают или, во всяком случае, работают не совсем так, как нам хотелось бы. Наконец, наблюдая за поведением наиболее популярных пользователей, ученые могут подсказать, как выделиться в растущей толпе онлайн-соискателей.
Я могла бы написать целую книгу о знакомствах в интернете и о том, что нового они могут рассказать нам о нас самих. К сожалению, придется ограничиться лишь одной главой, но, надеюсь, вы все-таки получите представление о том, как математика помогает в современном, технологичном, поиске любви.
