Числовые и функциональные ряды

1. Понятие числового ряда, его частичной суммы. Понятие сходящегося ряда и его суммы. Свойства сходящихся рядов. Необходимый признак сходимости ряда.

2. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения, признак Даламбера, интегральный признак. Условие сходимости ряда .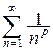

3. Понятие знакочередующегося ряда. Достаточный признак его сходимости. Знакопеременный ряд, достаточный признак его сходимости. Понятие абсолютно и условно сходящихся рядов.

4. Понятие функционального ряда и его области сходимости. Степенные ряды, радиус и область сходимости степенного ряда. Интегрирование и дифференцирование степенного ряда. Ряд Тейлора функции 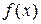. Разложение элементарных функций в степенные ряды.

5. Применения степенных рядов для приближенного вычисления значения функции, для вычисления определенного интеграла, для решения дифференциального уравнения.

6. Ряд Фурье периодической функции 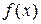. Ряды Фурье для четной и нечетной функций. Разложение в ряд Фурье функции, заданной на отрезке.

7.* Комплексная форма ряда Фурье. Амплитудный и фазовый спектры периодической функции.

8.* Представление непериодической функции интегралом Фурье в действительной и комплексной форме. Интеграл Фурье от четной и нечетной функции. Спектральная функция. Прямое и обратное преобразование Фурье.

Номера контрольных работ, которые необходимо выполнить во втором семестре, и номера задач соответствующих вариантов представлены в табл. 2.

Таблица 2

Номер варианта	Контрольная работа № 3 Номера задач	Контрольная работа № 4 Номера задач
	81 91 101 111	121 131 141
	82 92 102 112	122 132 142
	83 93 103 113	123 133 143
	84 94 104 114	124 134 144
	85 95 105 115	125 135 145
	86 96 106 116	126 136 146
	87 97 107 117	127 137 147
	88 98 108 118	128 138 148
	89 99 109 119	129 139 149
	90 100 110 120	130 140 150

III семестр

Для студентов всех специальностей, кроме экономических, гуманитарных

и физической культуры

Программа

Дифференциальное исчисление функции нескольких переменных

1. Определение и отыскание частных производных. Определение дифференцируемой функции. Дифференциалы первого и второго порядков. Понятие сложной функции и ее дифференцирование. Неявные функции и их дифференцирование. Касательная плоскость и нормаль к поверхности, их уравнения.

2. Безусловный экстремум функции. Глобальный экстремум функции в замкнутой ограниченной области. Условный экстремум функции.

3. Понятие скалярного поля. Поверхности и линии уровня скалярного поля. Понятие производной скалярного поля по направлению, формула для её вычисления. Определение градиента скалярного поля, свойства градиента.