D)Применим метод простой итерации
х = -cos ( x2 + 2). Тогда на интервале [0,1] выполняется условие |φ'(х)| < 0
|
Получим х = 0,985.
Задача №2
Порядок выполнения работы:
1. Составить таблицу значений функции f (x) и ее производных в узлах интерполяции.
2. Определить частичный интервал 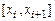 , содержащий точку х*, и соответствующие значения
, содержащий точку х*, и соответствующие значения  .
.
3. Вычислить значения 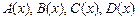 в точке х* по формулам:
в точке х* по формулам:
 (1)
(1)
4. Найти значение сплайна  в точке х*:
в точке х*:
 . (2)
. (2)
5. Вычислить значение 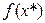 .
.
6. Вычислить значения 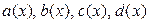 в точке х* по формулам:
в точке х* по формулам:
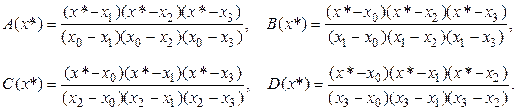 (3)
(3)
7. Найти значение многочлена Лагранжа  в точке х*:
в точке х*:
 . (4)
. (4)
8. Сравнить полученные результаты вычислений 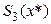 ,
,  ,
, 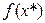 .
.
9. Найти абсолютную и относительную погрешности приближения 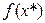 сплайном и многочленом Лагранжа.
сплайном и многочленом Лагранжа.
10. Построить график функции f (x) . Указать на графике точное и приближенные значения функции в заданной точке х*.
11. Сделать выводы.
Пример решения задачи №2.
Для функции  на интервале [1; 1,3] и узлов интерполяции с шагом h = 0,1 вычислить в точке х* =1,17:
на интервале [1; 1,3] и узлов интерполяции с шагом h = 0,1 вычислить в точке х* =1,17:
1) значение сплайна S3(x),
2) значение многочлена Лагранжа L3(x),
3) значение функции f (x).
Сравнить полученные результаты вычислений S3(x*), L3(x*) и f (x*). Найти абсолютную и относительную погрешности приближения f (x*) сплайном и многочленом Лагранжа. Построить график функции f(x). Указать на графике точное и приближенное значения функции в заданной точке х*. Вычисления производить с точностью до 0,00001.
Таблица 1 ГРАФИК ФУНКЦИИ
| i |  | ||||
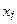 | 1,1 | 1,2 | 1,3 | ||
 | 1,4641 | 2,0736 | 2,8561 | ||
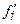 | 5,324 | 6,912 | 8,788 | ||
 = 1,4641 = 1,4641  = 2,0736 = 2,0736 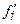 = 5,324 = 5,324 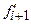 = 6,912 = 6,912 |
Таблица 2
 | 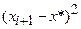 | 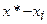 |  |  |  | 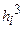 |
| 0,03 | 0,0009 | 0,07 | 0,0049 | 0,1 | 0,01 | 0,001 |
А(х*)=0,216 В(х*)=0,784 С(х*)=0,0063 D(x*)=-0,0147 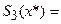 1,873883
1,873883 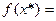 1,873887
1,873887
Таблица 3
| х*-х0 | х*-х1 | х*-х2 | х*-х3 | х1-х0 | х2-х0 | х3-х0 | х2-х1 | х3-х1 | х3-х2 |
| 0,17 | 0,07 | -0,03 | -0,13 | 0,1 | 0,2 | 0,3 | 0,1 | 0,2 | 0,1 |
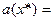 -0,0455
-0,0455 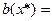 0,3315
0,3315 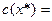 0,7735
0,7735 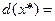 -0,0595
-0,0595 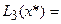 1,873841
1,873841
Погрешности приближения:
Абсолютные Относительные
 4,41×10-6
4,41×10-6  2,3534×10-6
2,3534×10-6
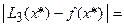 4,641×10-5
4,641×10-5  2,47667×10-5
2,47667×10-5
Вывод: Сплайн дает более точное приближение, чем многочлен Лагранжа.
Задача №3
Порядок выполнения работы:
1. Составить таблицу конечных разностей
| х | у | Dу | D2у | D3у | где 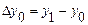 , , 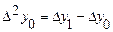 , , 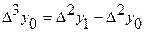 . . |
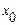 | 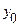 | ||||
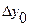 | |||||
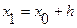 | 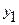 |  | |||
 | 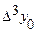 | ||||
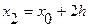 | 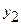 |  | |||
 | |||||
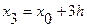 | 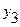 |
2. Вычислить производные  и
и 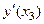 , используя
, используя
- Первую интерполяционную формулу Ньютона (для нахождения производных в точках, лежащих в начале таблицы значений 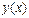 ):
):
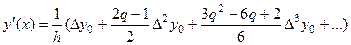 , (1)
, (1)
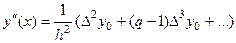 , где
, где  - шаг интерполяции; (2)
- шаг интерполяции; (2)
- вторую интерполяционную формулу Ньютона (для нахождения производных в точках, лежащих в конце таблицы значений 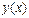 ):
):
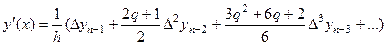 , (3)
, (3)
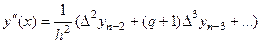 , где
, где  . (4)
. (4)
3. Вычислить производные  и
и 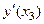 , используя интерполяционный многочлен Лагранжа для
, используя интерполяционный многочлен Лагранжа для 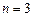 :
:
 . (5)
. (5)
4. Сравнить значения производных  и
и 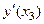 , полученных по различным интерполяционным формулам. Записать вывод.
, полученных по различным интерполяционным формулам. Записать вывод.
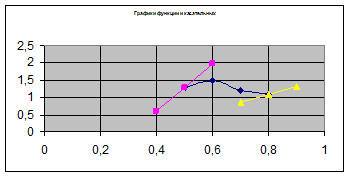
5. Построить график функции  и касательные к нему в точках
и касательные к нему в точках 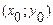 и
и 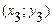 .
.
Пример решения задачи №3
Используя интерполяционные формулы Ньютона и Лагранжа, вычислить 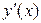 и
и 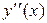 в точках
в точках 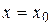 и
и 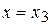 для функции
для функции 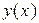 , заданной таблицей
, заданной таблицей
| x | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 1,3 | 1,5 | 1,2 | 1,1 |
Таблица 1. h = 0,1
| х | у | Dу | D2у | D3у | По формулам Ньютона:  6,83333 6,83333 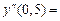 -120 -120 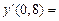 2,33333 2,33333 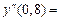 90 90 | По формулам Лагранжа:  6,8333 6,8333 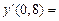 2,3333 2,3333 |
| 0,5 | 1,3 | |||||
| 0,2 | ||||||
| 0,6 | 1,5 | -0,5 | ||||
| -0,3 | 0,7 | |||||
| 0,7 | 1,2 | 0,2 | ||||
| -0,1 | ||||||
| 0,8 | 1,1 |
Таблица 2. Построение касательной в точке 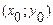 :
: 
| х | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| у | 1,3 | 1,5 | 1,2 | 1,1 | ||
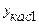 | 0,616667 | 1,3 | 1,983333 | |||
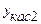 | 0,866667 | 1,1 | 1,3333 |
В градусах: В радианах:
 81,67435
81,67435  1,425486
1,425486
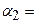 66,80141
66,80141 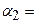 1,165905
1,165905