Теорема сложения вероятностей

Пусть в некотором испытании рассматриваются два случайных события
А и В, вероятности которых известны или могут быть найдены.

Теорема 5. Вероятность появления хотя бы одного из двух случайных событий равна сумме вероятностей этих событий без вероятности их совместного появления, т.е.

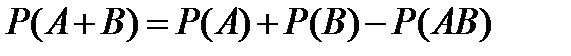(7)

Замечание. Если события А и В несовместны, то очевидно, что их произведение является невозможным событием, вероятность невозможного события равна нулю. Таким образом, формула (10.7) преобразуется в формулу для несовместных событий: .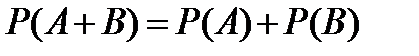

Пример 10. Два футболиста делают независимо друг от друга по одному удару по воротам. Вероятность попадания первого равна 0,8; второго – 0,9. Найти вероятность того, что произойдет хотя бы одно попадание.

Решение. Пусть событие А означает попадание первого футболиста, событие В – попадание второго футболиста. Тогда событие А+В означает, что произойдет хотя бы одно попадание. По теореме 5, получим:

. ■

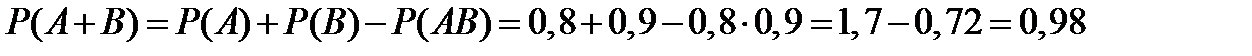Существует общая формула для нахождения вероятности суммы трех и большего числа совместных событий. Например, для трех событий А, В и С она имеет вид:

.

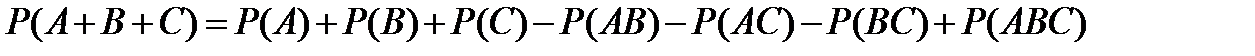Если число событий больше трех, то формула вероятности суммы событий еще более усложняется, поэтому стараются обойтись без нее. Для этого существует два пути:

− последовательно складывать события с применением формулы (10.7), т.е. вычислять 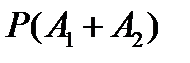, затем 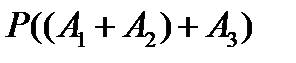и т.д.;

− перейти к противоположному событию.

Пример 11. Каждый из четырех стрелков независимо друг от друга производит по одному выстрелу в мишень. Вероятности попадания стрелков равны 0,7; 0,6; 0,8 и 0,4. Определить вероятность того, что произойдет хотя бы одно попадание.

Решение. Введем в рассмотрение следующие события:

А₁ – попадет первый стрелок;

А₂ – попадет второй стрелок;

А₃ – попадет третий стрелок;

А₄ – попадет четвертый стрелок.

По условию примера необходимо определить 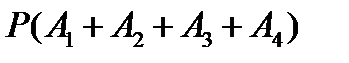. Найдем эту вероятность двумя способами.

В первом случае будем последовательно складывать события, и применять формулу (10.7), получим

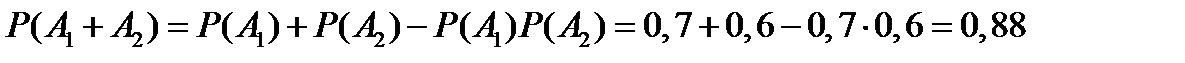
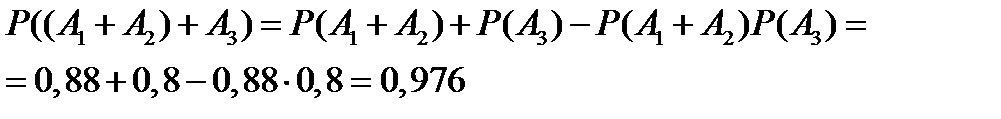
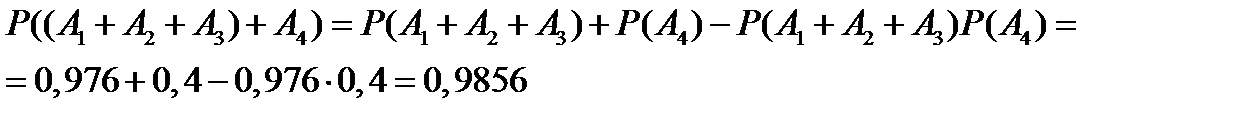
Во втором случае перейдем к противоположному событию. Для события 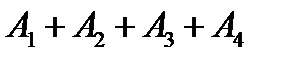противоположным является событие 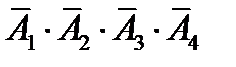, состоящее в том, что все четыре стрелка промахнутся. Так как вероятности промаха для каждого стрелка равны

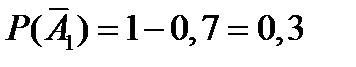
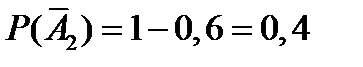
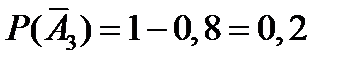
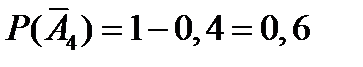, то

. ■

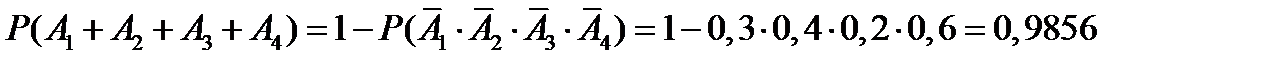Обобщая все вышеизложенное можно сформулировать следующее правило: если требуется найти вероятность суммы конечного числа совместных событий, при этом, известно, что противоположное к сумме событие состоит из меньшего числа исходов, то лучше вначале найти вероятность противоположного события, а затем прямого. Один из признаков, по которому можно почти безошибочно заключить, что стоит перейти к противоположному событию – это, если в вопросе задачи есть слово «хотя бы».

Теорема 6.Сумма вероятностей событий, образующих полную группу, равна 1.

Следствие. Сумма вероятностей противоположных событий равна 1, т.е.

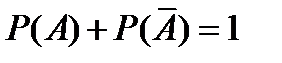(8)

где А и Ā – противоположные события.

При решение задач чаще применяется преобразованная формула (8),
а именно

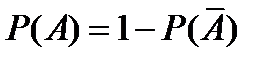(9)

В теореме сложения и во всех примерах использовалось понятие вероятности произведения, так называемых независимых событий.