Математические показатели надежности

Рассмотрим основные количественные показатели надежности на следующем примере. Предположим, что наблюдаются n₀= 1000 новых однотипных изделий, для которых следует определить параметры надежности. Условно примем, что все изделия начинают работать в момент t=0, по мере отказа изделия не восстанавливаются (например, лампы накаливания) и изымаются из наблюдаемой партии, но к t=1000ч эксплуатации все они выйдут из строя. В течение всего времени функционирования количество работоспособных изделий регулярно подсчитывается в конце каждого временного интервала, исчисляемого Dt=100ч. Наличие работающих элементов к моменту времени t_i, представлено в колонке 2 таблицы 4.1.

Таблица 4.1 – Распределение изделий и параметров надежности

t, ч	np(t)	Dn(Dt)	P(t)	F(t)	F(t)×10-3	l(t)×10-3
			1,00	0,00	0.00	0,000
			0.99	0,01	0,10	0,100
			0,97	0,03	0,20	0,202
			0,92	0,08	0,50	0,515
			0,81	0,19	1,10	1,195
			0,55	0,45	2,60	3,209
			0,28	0,72	2,70	4.909
			0,14	0,86	1,40	5,000
			0,06	0,94	0,80	5.714
			0,03	0,97	0,30	5,000
			0,00	1,00	0,30	10,000

Рассмотрим отказ как статистическое событие. При наличии достаточно большой выборки отказ - это случайное событие и в этом смысле носящее вероятностный характер. Именно такая трактовка на отказ как на событие, позволяет применять в теории надежности математический аппарат теории вероятности. В свете таких представлений, если n_р(t) - количество изделий, оставшихся в работоспособном состоянии к концу времени t, то n_от(t)=N₀ - n_p(t)- количество вышедших из строя изделий к моменту t. В то же время выражение:

Dn(Dt) = n_р(t) - n_p(t+Dt) (4.1)

позволяет рассчитать количество вышедших из строя изделий за интервал времениDt=t_i-t_i-1=100 ч (колонка 3 таблицы 4.1).

Надежность (или вероятность "выживания") в соответствии с определением вероятности для любого момента времени t [6] в течение испытания выражается отношением:

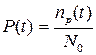. (4.2)

Возможна и другая запись уравнения (4.2):

. (4.3)

Величина Р(t) называется вероятностью безотказной работы или функцией надежности. В общем случае P(t) является функцией времени. Для нашего примера величина функции надежности для соответствующего времени t приведена в колонке 4 таблицы 4.1.

Так как событием, нарушающим безотказность работы, является отказ, то, по положению теории вероятности, вероятность отказа выражается формулой:

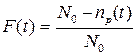(4.4)

и называется функцией отказов. Вполне очевидно, так как отказ и факт безотказной работы - взаимоисключающие события, то сумма вероятности их наступления должна быть равна единице, т. е.:

F(t) + P(t) = 1. (4.5)

Значения функции отказов для нашего примера приведены в колонке 5 таблицы 4.1. Записав уравнения (4.3, 4.5) в дифференциальной форме, получим одну из важнейших характеристик в теории надежности – плотность распределения отказов:

. (4.6)

Физический смысл параметра f(t) очевиден - он отражает скорость отказов, отнесенную к первичному количеству элементов, поставленных на испытание. Кроме того, крайне важно знать скорость отказов с учетом реально работающих в данный момент элементов, т.е. величину, определяемую выражением:

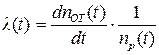. (4.7)

Этот параметр представляет собой интенсивность отказов и с учетом уравнения (4.6) может быть записан следующим образом:

. (4.8)

Иногда уравнения (4.6, 4.8) полезно представить в другом виде:

,

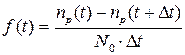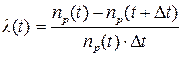. (4.9)

Уравнение (4.9) удобно для расчета динамики выхода из строя объектов наблюдения при условии, если известно, как изменяется интенсивность отказов. Действительно, оно может быть записано относительно n_р(t+Dt):

n_p(t+Dt) = n_p(t)×[1 - l(t)×D(t)]. (4.10)

При определенных условиях l(t)=l=const, и если можно назначить интервал наблюденияDt=const, то предыдущее уравнение может быть представлено в виде, удобном для расчетов:

n_p(t+Dt)= N₀×[1 - l×Dt]^Z, (4.11)

где z = (t+Dt)/Dt - порядковый номер временного интервала.

Установим связь между описанными выше характеристиками. На основании уравнений (4.6),(4.8) можно записать:

. (4.12)

Перепишем уравнение (4.9) в виде:

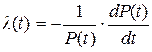. (4.13)

Разделяя переменные, запишем:

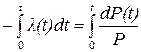. (4.14)

Проинтегрировав, получим:

. (4.15)

Из уравнения (4.6) с учетом уравнения (4.5) можно записать:

. (4.16)

Это означает, что вероятность отказа F(t)за время t равно площади под кривой плотности распределения f(t)в интервале от 0 до t. Если необходимо рассчитать вероятность отказа на каком-либо временном отрезке Dt=t₂-t₁, то она будет равна:

F(Dt) = F(t₁) - F(t₂), (4.17)

что может рассматриваться как часть площади под кривой f(t) на участке от t₁ до t₂.