Важные классы неоднородных марковских процессов

1) Марковский процесс, определенный на множестве Т, состоящем только из целых чисел, - т.е. марковская последовательность x_n - называется, согласно традиции, цепью Маркова (или марковской цепью).

2) Особенно просты дискретные цепи Маркова, т.е. те, для которых Х - конечное или счетное множество.

3) Среди дискретных цепей выделяются конечные цепи, для которых фазовое пространство конечно.

Для дискретных цепей Маркова достаточно задать счетный (или конечный) набор чисел - меры (вероятности) всех одноточечных множеств. Поэтому переходная функция определяется заданием матрицы вероятностей перехода (или переходной матрицы) P^st, зависящей от двух моментов времени s£t:

P^st=|| p(s, i, t, j)=p_st (i, j) || i, jÎX.

p(s, i, t, j)=P(s, i, t, {j})

Элементы матрицы мы обозначим буквой p, строки и столбцы нумеруем элементами из Х. Величина p(s, i, t, j) имеет смысл обычной условной вероятности P{x_t=j|x_s=i}.

Требование, налагаемое на переходную функцию, чтобы она была распределением вероятностей, превращается в требование того, чтобы матрица P^st была стохастической или вероятностной, т.е. состояла из неотрицательных элементов с суммой 1 в каждой строке:

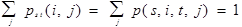
Условие P(s, x, s, Г) = d_x(G) превращается в условие P^ss=E - единичная матрица.

Еще раз отметим, что для цепей Маркова время - это только целые моменты времени!!!

Уравнение Чепмена-Колмогорова для процессов с дискретным фазовым пространством превращается в

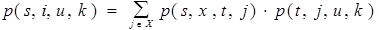
или (в другой форме записи)

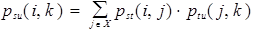
Это обозначает, что соответствующие матрицы перемножаются.

P^su = P^st P^tu

Для цепей Маркова достаточно задать набор вероятностей перехода за один шаг

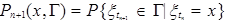
Действительно

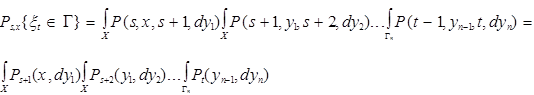
Для дискретных цепей Маркова это свойство выглядит как

P^st=P^s,s+1P^s+1,s+2...P^t-1,t=P_s+1P_s+2...P_t

4) Марковские процессы с непрерывным временным параметром (Т=[0, ¥) или (-¥, ¥)), но с конечным или счетным Х. Их иногда называют дискретными цепями Маркова с непрерывным временем.