Визначник суми матриць

Нехай потрібно знайти визначник суми С = А + У двох квадратних матриць n-го порядку. Представимо визначник цієї суми через стовпці матриць, що складаються:

У відповідності з властивістю лінійності визначника щодо стовпців (3) запишемо:

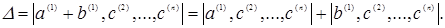
Застосовуючи цю властивість щодо других стовпців отриманих визначників, маємо:

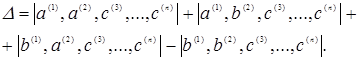
Продовжуючи цей процес до останніх стовпців включно, одержуємо розкладання в суму, що містить визначники матриць, що складаються, det A і det У, а також визначники, утворені зі стовпців матриць А і В усіма можливими сполученнями, причому стовпці в таких визначниках займають ті ж місця, що вони, займали в матрицях А і В. Це можна виразити співвідношенням:

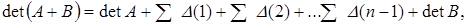
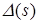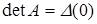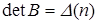де — визначник, отриманий заміщенням s стовпців визначника першої матриці відповідними стовпцями другої матриці. Знаки сум означають, що складаються визначники для всіляких сполучень s стовпців, що заміщаються. Оскільки і , можна запропонувати більш короткий запис:

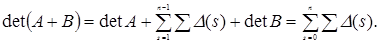
Скориставшись розкладанням Лапласа (5) для визначників 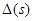по s заміщених стовпцях, одержимо інший вираз для визначника суми двох матриць:

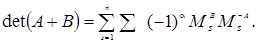
У силу комутативності додавання матриць байдуже, яку з матриць A і У вважати першої і яку — другий. Отримані розкладання через свою складність непридатні для практичних обчислень визначників, але вони можуть бути корисні при доказі різних співвідношень. Зокрема, вони дозволяють виразити речовинну і мниму частини визначника комплексної матриці:

де т = 1/2п — для парних п; т = 1/2(п — 1) — для непарних п..

Застосуємо ці формули для обчислення визначника комплексної матриці:

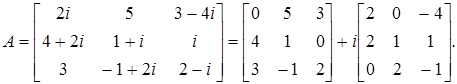
Для речовинної і мнимої частин визначника det А маємо:

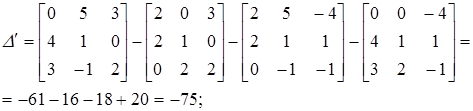
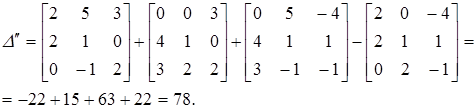
Таким чином, , що можна перевірити безпосереднім обчисленням визначника.

Розкладання визначника суми двох матриць можна узагальнити для будь-якої кількості квадратних матриць того самого порядку. Так, для трьох матриць маємо:

,

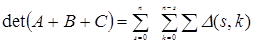де через 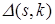позначені визначники, утворені всіма можливими заміщеннями стовпців визначника першої матриці s стовпцями другої матриці і k стовпцями третьої матриці.