Операторный метод анализа систем

Данный метод основан на представлении входного и выходного сигнала посредством преобразования Лапласа, которое является обобщением преобразования Фурье на плоскость комплексной частоты.

Изображения по Лапласу во всех точках комплексной плоскости р, за исключением счетного множества так называемых особых точек, являются аналитическими функциями. Особые точки – как правило, однократные или многократные полюса. На практике широко используют таблицы преобразований Лапласа. Основные свойства преобразования Лапласа аналогичны свойствам преобразования Фурье.

Важнейшей характеристикой, на которой основан операторный метод, является отношение изображений выходного и входного сигналов:

K(p) = U_вых(р)/U_вх(р), (3)

называемое передаточной функцией или операторным коэффициентом передачи рассматриваемой системы.

В соответствии с (3) из дифференциального уравнения, описывающего систему, можем получить вид передаточной функции, аналогичный формуле (1) для частотного коэффициента передачи системы:

(4)

Таким образом, передаточная функция есть обобщение частотного коэффициента передачи системы на плоскость комплексной частоты р и обладает физическим смыслом и всеми свойствами последнего.

В рамках операторного метода передаточная функция является полной математической моделью системы. Если эта функция известна, то поиск выходной реакции системы на заданное входное воздействие разбивается на три этапа:

1. и_вх(t) ® U_вх(р),

2. U_вых(р) = К(р) U_вх(р),

3. U_вых(р) ® и_вых(t).

ЗАДАНИЕ. Для предложенного варианта линейной цепи и заданных параметров:

1. Определить вид дифференциального уравнения, описывающего данную цепь, относительно именно тех входных и выходных параметров, которые указаны на схеме.

2. Найти частотный коэффициент передачи, его модуль и аргумент.

3. Построить графики АЧХ и ФЧХ данной системы.

4. Найти частотный коэффициент передачи мощности.

5. Определить передаточную функцию системы.

6. Найти импульсную и переходную характеристики; построить их графики.

7. Найти отклик цепи на прямоугольный импульс с амплитудой Е и длительностью t_и временным, классическим, спектральным и операторным методами; сравнить полученные разными методами результаты.

ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТОВ:

Варианты:

1.

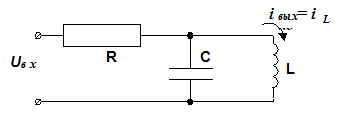
2.

3.

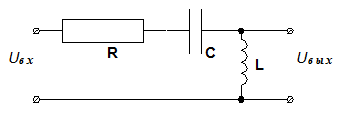
4.

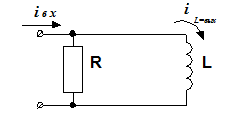
5.

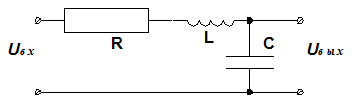
6.

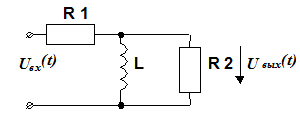
7.

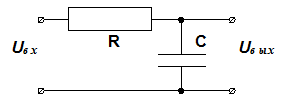
8.

9.

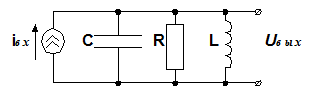
10.

11.

12.

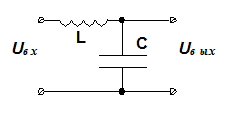
Таблица соответствий вариантов и параметров:

Вариант	Параметры
R, Ом	L, мГн	С, мкФ	Е, В	τи , с
1.		0,5
2.
3.		0,4

Примечание: Если в схеме два одинаковых элемента, то считать R₁ = 2R₂; L₁ = 2L₂;

C₁ = 2C₂.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. При каких условиях реакцию линейной системы на короткий входной импульс можно считать импульсной характеристикой системы?

2. Сформулируйте условие физической реализуемости системы.

3. Как связаны между собой импульсная характеристика системы и ее частотный коэффициент передачи?

4. Какими способами можно определить частотный коэффициент передачи линейной стационарной системы? Выберите из них оптимальный, на Ваш взгляд, способ.

5. В чем состоит отличие динамических систем от стационарных?

6. В каких случаях и почему для анализа системы удобнее использовать частотный коэффициент передачи мощности?

7. При каких условиях RC-цепь можно считать дифференцирующей, а при каких – интегрирующей?

8. Исследуйте аналогичные условия (дифференцирования и интегрирования) для RL-цепи.

9. Проанализируйте и оцените достоинства и недостатки временного, спектрального и операторного методов анализа линейных стационарных систем.

ЛИТЕРАТУРА

1. Попов В. П. Основы теории цепей. – М.: Высшая школа, 2000.

2. Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1999.

3. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 1988.

4. Основы теории электрических цепей и электроники: Учебник для ВУЗов/ В.П.Бакалов, А.Н.Игнатов, Б.И.Крук. – М: Радио и связь, 1989.

5. Каяцкас А. А. Основы радиоэлектроники. - М., Высшая школа, 1988.

6. Бирюков В. Н. Попов В. П. Семенцова В. И. Сборник задач по теории цепей. – М.: Высшая школа, 1998.

7. Шебес М. Р. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990