Операции над множествами, их свойства.
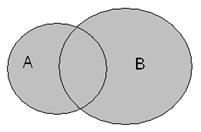
Определение 1. Пересечениеммножеств А и В называется множество, обозначаемое А∩В, состоящее из всех элементов, принадлежащих и множеству А и множеству В одновременно.
Для наглядности будем использовать так называемые диаграммы Эйлера- Вена.

А∩В
 Определение 2. Объединением множеств А и В называется множество, обозначаемое А
Определение 2. Объединением множеств А и В называется множество, обозначаемое А 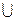 B,состоящее из всех элементов, принадлежащих хотя бы одному множеству А или В.
B,состоящее из всех элементов, принадлежащих хотя бы одному множеству А или В.
А 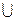 В
В
Определение 3.Множества называются непересекающимися, если их пересечение равно пустому множеству.
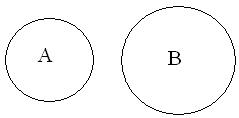
A  Ø.
Ø.
Определение 4. Разностьюмножеств А и В называется множество, обозначаемое А\B, состоящее из всех элементов множества А, не принадлежащих множеству В.
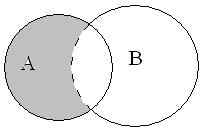
А\B
Под универсальным множеством будем понимать такое множество U,что все рассматриваемые множества являлись подмножествами U.
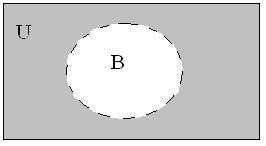 Определение 5.Разность U\B называется дополнениемко множеству В и обозначается.
Определение 5.Разность U\B называется дополнениемко множеству В и обозначается.
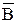
Из определения ясно, что 1) В 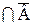 =Ø; 2)
=Ø; 2)  =U.
=U.
Теорема 1.Для произвольных множеств А ,В и С справедливы следующие свойства:
1. Коммутативность пересечения и объединения:
 .
.  ;
;
2. Ассоциативность пересечения и объединения:
 ;
; 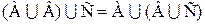 ;
;
3. Дистрибутивность пересечения относительно объединения:
 ;
;
Дистрибутивность объединения относительно пересечения:
 ;
;
4. Идемпотентность пересечения и объединения:
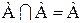 ,
, 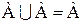 ;
;
5. 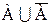 =U;
=U; 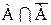 =Ø
=Ø
6. Законы де Моргана:
 =
= 
 ;
;  =
= 
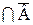
7. Законы поглощения:
 U;
U; 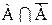 =Ø;
=Ø;
 U=U;
U=U;  ;
;
 Ø=A;
Ø=A;  Ø= Ø;
Ø= Ø;
8. 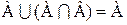 ;
; 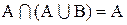
9. Закон инволюции:  =
= 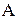
10. Закон исключения разности:  .
.
Доказательство(с помощью определений)
1. Свойство 1 выполняется, т.к. по определению операции пересечения , левая часть А  есть множество всех элементов, принадлежащих А и В одновременно, а правая часть
есть множество всех элементов, принадлежащих А и В одновременно, а правая часть  есть множество всех элементов, принадлежащих В и А одновременно. Отсюда следует, что левая и правая части состоят из одних и тех же элементов. Свойства 1 и 2 доказываются аналогично. Докажем свойство 6:
есть множество всех элементов, принадлежащих В и А одновременно. Отсюда следует, что левая и правая части состоят из одних и тех же элементов. Свойства 1 и 2 доказываются аналогично. Докажем свойство 6:  =
= 
 . Пусть
. Пусть  Y=
Y= 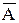
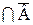 . Пусть x
. Пусть x 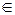 X. Тогда, по определению x
X. Тогда, по определению x  и
и 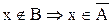 и
и 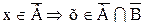 , , т.е.X
, , т.е.X 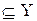 (1).
(1).
Пусть теперь y 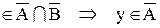 и
и  и
и 
 в силу произвольности выбора y, все элементы множества Y принадлежат X, т.е
в силу произвольности выбора y, все элементы множества Y принадлежат X, т.е 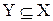 (2).
(2).
Из (1) и (2) X=Y,т.е. 
Остальные свойства доказываются аналогично.
Замечание 1.Операции объединения и пересечения можно распространить на любую совокупность множеств.
Пусть A1, A2, … , An-множества. Пересечениеммножеств A1, A2, … ,An называется множество С, обозначаемое С=  , состоящее из всех элементов, принадлежащих каждому из множеств A1, A2, … ,An.
, состоящее из всех элементов, принадлежащих каждому из множеств A1, A2, … ,An.
Аналогично, объединениеммножеств А1, A2, … , Аn называется множество С, обозначаемое С= 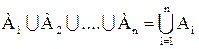 , состоящее из всех элементов, принадлежащих хотя бы одному из множеств А1, A2, … , Аn .
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А1, A2, … , Аn .
Справедливы обобщенные дистрибутивные законы:
 и
и 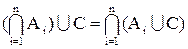 ,
,
а также обобщенные законы де Моргана:
 и
и 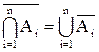 .
.
Замечание 2.Не трудно показать, что если А, В и С- конечные множества, то:
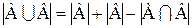 и
и  .
.
