Реакции шероховатых связей. Угол трения.

Лекция №7. Равновесие тела при наличии трения.

Равновесие тела при наличии трения скольжения.

При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения скольжения, которая может принимать значения от 0 до значения 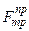, называемого предельной силой трения (это такое максимальное значение силы трения, при котором материальное тело еще остается в состоянии равновесия).

Равновесие, имеющее место, когда сила трения равна 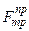называется предельным равновесием.

Предельная сила терния численно равна произведению коэффициента трения на нормальное давление.

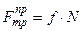. (7.1)

Направлена сила трения в сторону противоположную той, куда действующие на тело силы стремятся его сдвинуть.

Коэффициент трения 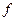- величина безразмерная; зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность и т.п.).

При равновесии 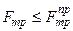, т.е.

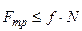. (7.2)

Случай строго равенства в (7.2) отвечает максимальному значению силы трения. Это значит, что значение силы трения можно вычислять по формуле (7.1) только если заранее известно, что имеет место критический случай. Во всех других случаях силу трения следует определять из уравнений равновесия.

Реакции шероховатых связей. Угол трения.

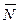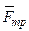Реакция реальной (шероховатой связи) складывается из двух составляющих: нормальной реакции и силы тре ния . Следовательно, полная реакция 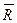будет отклонена от поверхности на некоторый угол. При изменении силы трения от 0 до 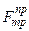сила 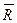изменяется от 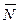до 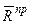, а ее угол с нормалью растет от 0 до некоторого предельного значения 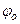(рис. 7.1).

Наибольший угол 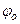, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения.

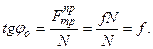(7.3)

При равновесии полная реакция 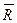в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол .

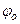Если к телу, лежащему на шероховатой поверхности, приложить силу 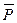, образующую с нормалью угол 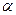(рис. 7.2), то тело сдвинется только тогда, когда сдвигающее усилие 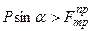. Пренебрегая весом тела, получим,

,

,

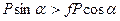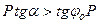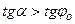, т.е. .

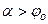Следовательно, никакой силой, образующей с нормалью угол 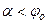, сдвинуть тело вдоль данной поверхности нельзя.

Пример 1. Найти при каком наибольшем угле наклона 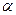(рис. 7.3) тяжелый груз, лежащий на наклонной плоскости, остается в равновесии, если коэффициент трения груза о плоскость равен .

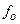На груз в рассматриваемом предельном положении действует сила тяжести 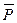, нормальная реакция 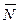и предельная сила трения 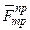. Составим уравнения равновесия в проекциях на ос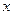и и 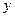. Будем иметь:

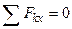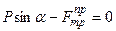; ; (1)

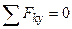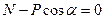; . (2)

Из (2) находим

,

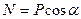тогда

.

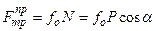Подставляя это значение в (1), получим

.

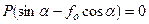Отсюда, с учетом (7.3),

.

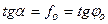Следовательно, наибольший угол наклона, при котором возможно равновесие, равен углу трения.