Расчет передаточной функции дифракционной решетки в приближении Кирхгофа

Простейшая фазовая дифракционная решетка представляет собой зеркально отражающий элемент, поверхность которого имеет протяженный рельеф, не зависящий от одной из координат и периодический по другой координате (рис.3.1.). Оптическое излучение, отражаясь от такого элемента, приобретает дополнительную фазу, которая обусловливает желательный эффект преобразования излучения. Как правило, дифракционные решетки используются для создания различных диаграмм направленности - распределений интенсивности излучения в данной зоне. В приближении Кирхгофа диаграмму направленности, излучения, волновое поле которого в плоскости Z=0 есть 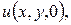можно получить, вводя вместо переменных 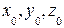- координат точки наблюдения в формуле Кирхгофа (вставить интеграл Кирхгофа) - новые переменные

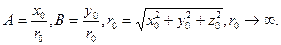(3.3)

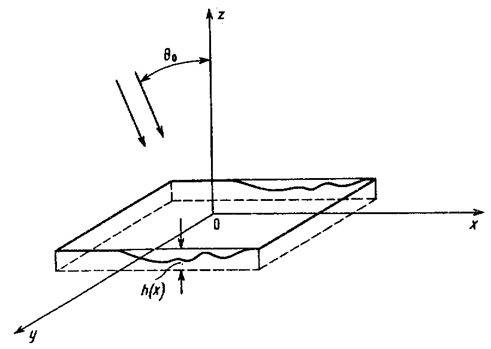
Рис. 3.1. Рельеф отражающей дифракционной решетки

Раскладывая при 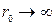величину

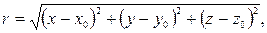
получаем 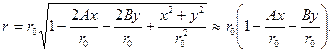(3.4)

Если теперь пренебречь в знаменателе формулы Кирхгофа членами первого порядка малости, а в показателе экспоненты - членами второго порядка, то выражение для поля при 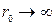может быть записано в виде

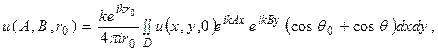(3.5)

где 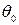- угол падения исходного излучения на оптический элемент;

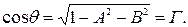(3.6)

Таким образом. А, В, Г- направляющие косинусы вектора, выходящего из начала координат в точку наблюдения (рис. 3.2). При 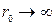последнее выражение, очевидно, стремится к нулю. Диаграммой направленности поля излучения называют величину:

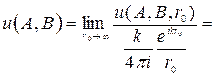
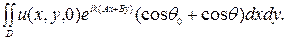(3.7)

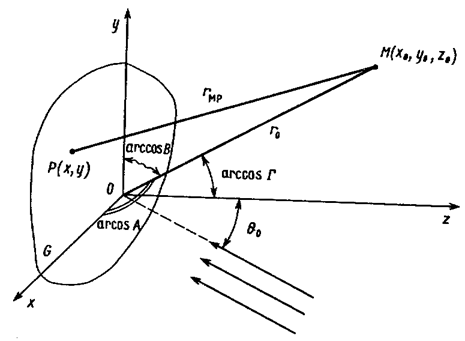
Рис. 3.2. К определению диаграммы направленности

Во многих случаях именно диаграмма направленности является той необходимой для нас передаточной функцией, которая позволяет определить параметры чувствительности по углу и длинам волн дифракционной решетки.

Вычисление диаграммы направленности сводится фактически к определению преобразования Фурье от волнового поля в плоскости Z= 0.

Поскольку рельеф дифракционной решетки не зависит от переменной y, то, если исходное волновое поле также не зависит от y, задача вычисления диаграммы направленности волнового поля является фактически одномерной, причем

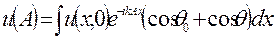(3.8)

При этом А изменяется в пределах от -1 до 1, значение A = 0 соответствует наблюдению со стороны нормали в плоскости дифракционной решетки, 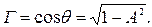Интеграл в (3.8) берется по интервалу, включающему в себя дифракционную решетку (рис. 3.3). Для характерных дифракционных задач величина D значительно превосходит период d решетки, что обусловливает специфику вычисления интеграла (3.8).

Выражение (3.8) допускает простую интерпретацию на основе принципа суперпозиции для решения линейного дифференциального уравнения Гельмгольца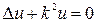

Применим для решения уравнения Гельмгольца метод разделения переменных, т.е. будем искать его решение в виде 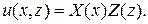Подставляя это выражение в уравнение и разделяя переменные, получим:

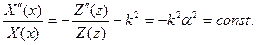
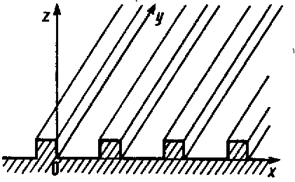
Рис. 3.3. Одномерная дифракционная решетка

Отсюда сразу находим X(x) = Ae^-ikαx, α может принимать любые положительные и отрицательные значения. Соoтветствующие функции Z(z) будут иметь вид 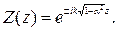Таким образом, получаем следующие частные решения уравнения Гельмгольца:

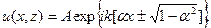(3.9)

При 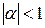последнее выражение описывает плоскую волну, распространяющуюся в направлении, определяемом направляющими косинусам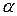и и 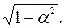При этом перед корнем необходимо брать знак "+", поскольку именно такое выражение описывает волну, распространяющуюся в положительном направлении. При 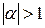выражение (3.9) описывает поверхностные волны, не распространяющиеся в бесконечность, а затухающие при 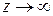экспоненциально (при соответствующем выборе знака в (3.9)). В общем случае поле, удовлетворяющее уравнению Гельмгольца, может быть представлено, в виде суперпозиции рассмотренных простейших решений

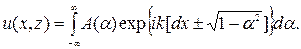(3.10)

Полагая здесь Z=0, получаем

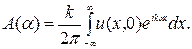
Сравнивая последнее выражение с (3.8), видим, что диаграмма направленности определяется разложением решения уравнения Гельмгольца с соответствующими граничными условиями и условиями излучения на бесконечности на плоские волны, распространяющиеся в различных направлениях.

Для того чтобы рассчитать диаграмму направленности, создаваемую дифракционной решеткой, необходимо тем или иным способом определить отраженное поле в плоскости оптического элемента Z=0. Воспользуемся для этого приближением геометрической оптики. Пусть дифрак­ционный элемент имеет вид штрихов, протяженных вдоль оси Oy. Профиль оптического элемента вдоль оси Оx описывается функцией h(x), имеющей смысл высоты рельефа. На описанный дифракционный элемент падает излучение под углом 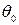к нормали (рис. 3.4). Волновое поле, описывающее такое падающее излучение, имеет вид:

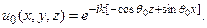
Считаем, что отражённое волновое поле в плоскости Z =0 имеет вид

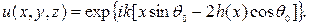(3.11)

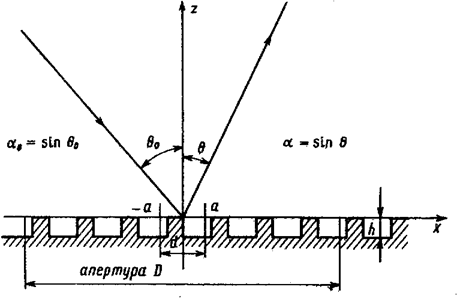
Рис. 3.4. Формирование отражающим рельефом дополнитель­ного набега фаз (фазовой функции)

Выражение (3.11) можно интерпретировать следующим образом. Излучение, падающее на элемент в точке (X, 0), отражается от поверхности рельефа на глубине h(x), как от плоской поверхности. Разумеется, применимость выражения (3.11) ограничена случаем, когда период решетки значительно превосходит ее глубину, а также длину волны используемого излучения, 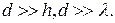Приняв выражение (3.11) для отраженного поля для вычисления диаграммы направленности остается вычислить интеграл (3.8).

Выражения (3.8) и (3.11) не учитывают специфику дифракционных решеток, связанную с их периодичностью, и их можно применять для определения диаграмм направленности любых оптических элементов с достаточно простой струк­турой. Учтем теперь явную периодичность структуры дифракционной решетки. Пусть d - период решетки, т.е.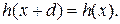

Считаем, что на апертуре элемента D укладывается целое число периодов дифракционной решетки. Пусть

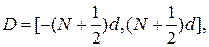т. е. апертура включает в себя N+1 периодов дифракционной решетки.

Обозначим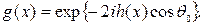

158-171

М - четное,

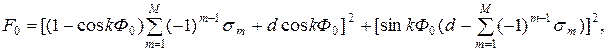
М - нечетное,

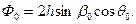(14)

Из (12) и (13) следует, что соотношение интенсивностей в ненулевых порядках не зависит от глубины рельефа решетки h. В то же время интенсивность излучения в нулевом рорядке зависит от h. Таким образом, мы можем, выбирая параметры 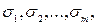добиться равенства интенсивностей в ненулевых порядках 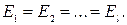Затем, изменяя глубину рельефа h, можно сравнять интенсивности излучения в нулевом и ненулевом порядках.

Описанная выше скалярная модель дифракционной решетки может быть с минимальными изменениями использована также для расчета диэлектрических решеток -делителей лазерного пучка. В [16] рассчитаны оптические элементы, работающие на прохождение в оптическом диапазоне для случая нормального падения излучения. Для выбора параметров 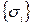используется специальный итерационный алгоритм. Особенностью рассмотренной модели является требование применимости приближения скалярного волнового поля, а именно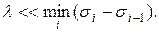

При выполнении этого условия период решетки d будет значительно больше длины волны 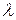, следовательно, количество распространяющихся порядков очень велико. Поэтому при синтезе делителя на небольшое число порядков требуется обеспечить малые значения интенсивности в старших порядках и примерно равные - в младших.

В табл. 3.1 приведены результаты расчетов из [16], полу­ченные описанным выше способом.

Таблица 3.1

M
s
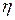,%	84,5	76,0	71,0	63,7	64,9	70,3	68,0	65,1

Малые значения эффективности решеток 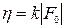(k -общее число равных по интенсивности порядков) обусловлены наличием большого числа побочных порядков. Повысить эффективность можно, выбрав период решетки d таким, чтобы число распространяющихся порядков соответствовало требуемому коэффициенту деления. Однако в этом случае скалярная модель перестает адекватно описывать рассеяние волны на решетке и существенно ужесточаются требования к технологии изготовления решеток. Это приводит к необходимости использования более точной модели дифракционных решеток, построенной на основе электродинамических уравнений Максвелла, а также к совершенствованию или созданию принципиально иных методов их изготовления.