Б) фронтально-проецирующей плоскостью

Сечение сферы плоскостью всегда является окружностью. Если секущая плоскость параллельна плоскости проекций, то такая окружность проецируется на эту плоскость без искажения. Если же она не параллельна – проекция сечения представляет собой эллипс.

На рисунке рассмотрен пример пересечения сферы τ плоскостью α, параллельной плоскости π1, и фронтально - проецирующей плоскостью β.

Сечение сферы плоскостью α проецируется на плоскость π1 в виде окружности n’ радиусом, равным отрезку [C’’6’’]. Горизонтальные проекции точек 5 и 51 находят по принадлежности окружности параллели n, профильные –

координатным способом. Проекции точек 1 и 6, лежащих на главном фронтальном меридиане, строят по принадлежности меридиану.

Сечение сферы плоскостью β проецируется на горизонтальную и профильную плоскости проекций соответственно эллипсами m’ и m’’’. Опустив перпендикуляр из фронтальной проекции центра сферы O’’ на фронтальную проекцию сечения плоскостью β, получают проекции точек C’’1≡3’’≡3’’1, где C’’1 – фронтальная проекция центра окружности m. Проекции точки С1 на горизонтальной и профильной плоскостях проекций находят по принадлежности оси симметрии. Проекции точек 3 и 31 на плоскости π1 строят, используя параллель сферы. Профильные их проекции получают координатным способом.

Точки 2 и 21 лежат на экваторе сферы. Вначале строят их горизонтальные

проекции (по принадлежности экватору сферы), затем профильные, используя в

качестве вспомогательной линии параллель сферы, проходящую через точки 2

и 21 и лежащую в профильной плоскости уровня - профильную параллель.

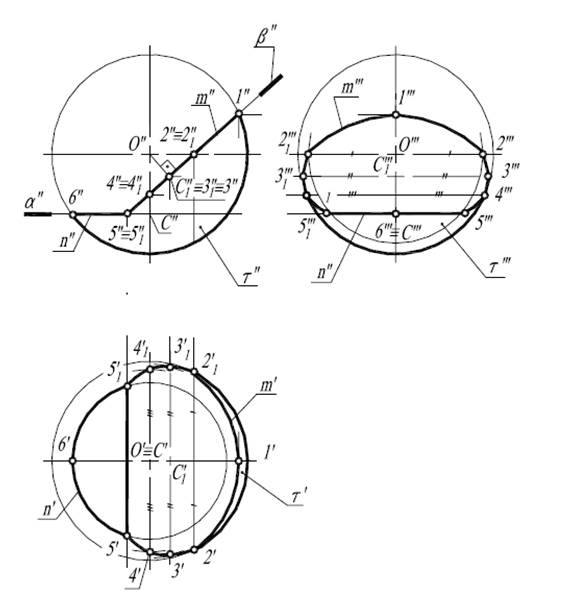
Пересечение сферы плоскостями α и β

Точки 4 и 41 лежат на главном профильном меридиане, по принадлежности которому находят их профильные проекции. Для построения горизонтальных проекций этих точек используют параллель сферы.