В классической электронной теории
1. Закон Ома. Пусть в металлическом проводнике существует однородное электрическое поле напряженностью Е. Со стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a = F/m = eE/m . Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость Vmax = eE<τ>/m, где <τ> - среднее время между двумя последовательными столкновениями электрона с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в электрическом поле энергию и останавливается. Следовательно,
<V> = (Vmax +0)/2 = eE<t>/(2m). (5)
Классическая теория металлов не учитывает распределения электронов по скоростям (распределение Ферми-Дирака), поэтому <τ> вычисляется по формуле:  . А так как
. А так как 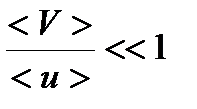 ,
,
то  . (6)
. (6)
Подставляя (6) в (5), получим
<V> = eE<l>/(2m<V>). (7)
Тогда плотность тока
 (8)
(8)
где  - (9)
- (9)
удельная электропроводность металла. Таким образом, получили закон Ома.
2. Закон Джоуля-Ленца. К концу свободного пробега электрон под действием электрического поля приобретает дополнительную кинетическую энергию
 . (10)
. (10)
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т.е. на его нагревание.
За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений:
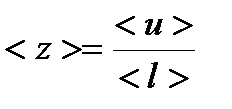 . (11)
. (11)
Если n – концентрация электронов, то в единицу времени происходит n <z> столкновений в единице объема и решетке передается энергия
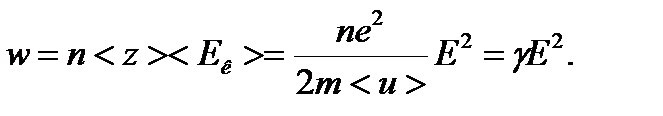 (12)
(12)
Формула (12) выражает закон Джоуля-Ленца для удельной тепловой мощности тока.
