Дифференциальные уравнения

Основные понятия

Определение 6.4.1.Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется обыкновенным дифференциальным уравнением.

Определение 6.4.2. Порядком дифференциального уравнения называется порядок старшей производной, входящей в данное уравнение.

Например, уравнение 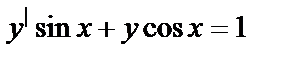- первого порядка; 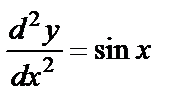- второго порядка; 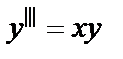- третьего порядка и т. д.

Решением дифференциального уравнения называется функция y=y(x), удовлетворяющая этому уравнению. График решения на плоскости xOy называется интегралом уравнения.

Процесс нахождения решения называется интегрированием дифференциального уравнения.

Если решение уравнения получено в неявном виде 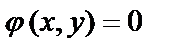, то оно обычно называется интегралом уравнения.

Задача Коши для уравнения

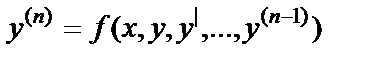(6.4.1)

ставится следующим образом. Среди всех решений уравнения (6.4.1) требуется найти решение y=y(x), для которого функция y(x) вместе со своими производными до (n-1)-го порядка включительно принимает заданные значения 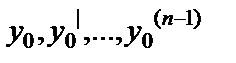при заданном значении x₀ аргумента x, т.е.

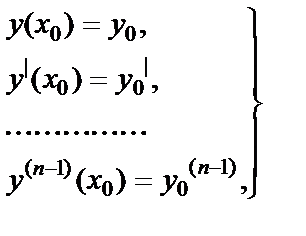(6.4.2)

где x₀, y₀, y₀^|,…,y₀^(n-1) – заданные числа.

Условия (6.4.2) называются начальными условиями решения y=y(x), а само это решение – частным решением уравнения (6.4.1), удовлетворяющим начальным условиям (6.4.2).

Общее решение уравнения (6.4.1) – это решение вида 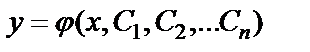, зависящее от n произвольных постоянных C₁, C₂, …C_n, которые можно подобрать таким образом, чтобы удовлетворить любой системе начальных условий.

Частное решение уравнения (6.4.1) может быть получено из общего решения при некоторых числовых значениях произвольных постоянных C₁, C₂, …C_n.

Уравнения с разделяющимися переменными

Дифференциальное уравнение с разделяющимися переменными имеет вид

M₁(x)N₁(y)dx+M₂(x)N₂(y)dy=0. (6.4.3)

Поделив обе части уравнения (6.4.3) на N₁(y)M₂(x), получим уравнение

,

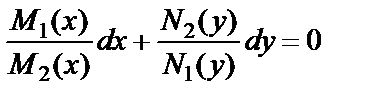в котором переменные разделены. Общий интеграл уравнения находится почленным интегрированием:

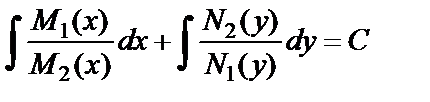
Однородные уравнения

Уравнение вида

y^|=f(y/x) (6.4.4)

называется однородным уравнением.

Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y=ux, где u – новая искомая функция. Дифференцируя равенство y=ux, получим

.

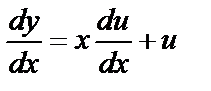Подставив y и 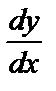в уравнение (6.4.4), получим

,

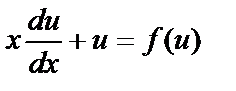Откуда

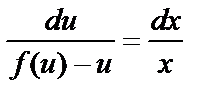. (6.4.5)

Это уравнение с разделяющимися переменными u и x. Найдя общее решение (интеграл) уравнения (6.4.5) и заменив u на y/x, получим общее решение (интеграл) данного однородного уравнения.

Линейные уравнения

Дифференциальное уравнение называется линейным, если оно линейно (т.е. первой степени) относительно искомой функции y и ее производной 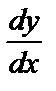. Общий вид линейного уравнения

y^|+P(x)y=Q(x). (6.4.6)

Линейное уравнение сводится к двум уравнениям с разделяющимися переменными, если искомую функцию y заменить произведением двух вспомогательных функций u и v, т.е. положить y=uv. Тогда

,

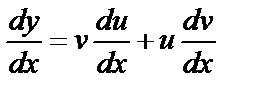и данное уравнение (6.4.6.) примет вид

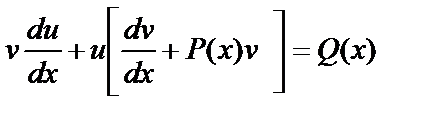. (6.4.7)

Пользуясь тем, что одну из вспомогательных функций, например v, можно выбрать произвольно, подберем ее так, чтобы выражение в квадратных скобках обратилось в нуль, т.е. в качестве v возьмем одно из частных решений v=v(x) уравнения с разделяющимися переменными

.

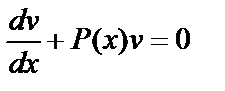Подставляя выражение v=v(x) в уравнение (6.4.7), получаем уравнение относительно функции u:

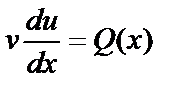, (6.4.8)

которое также является уравнением с разделяющимися переменными. Найдя общее решение уравнения (6.4.8) в виде u=u(x,C), получим общее решение линейного уравнения (6.4.6):

y=u(x,C)v(x).