Оценка остаточного члена в формуле Тейлора

ИКТИБ ИТА ЮФУ

КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ

Лекция 19 Формула Тейлора

Формула Тейлора

Как мы с вами уже отмечали, рычагом к созданию в 17, 18 веках теории дифференциального исчисления явилось необходимость приближения сложной функции более простыми функциями. В качестве таких простых функций английский математик Брук Тейлор (1685-1731) стал использовать многочлены.

Рассмотрим многочлен степени , определяемый параметрами: . Пусть задана функция , имеющую производных в точке . Рассмотрим чисел: , , , …, . Они однозначно определяют многочлен Тейлора степени не выше , обладающий тем свойством, что , ,…, :

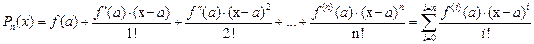(1)

Многочлен Тейлора (1) и его производных совпадают в точке с функцией и ее производными. Разумно предположить, что многочлен Тейлора (1) приближает функцию в окрестности точки . Этот факт отражается формулой

, (2)

которая называется формулой Тейлора. При формула Тейлора (2) принимает вид (3) и называется формулой Маклорена.

Обратите внимание, что формула Тейлора (2) не нуждается в доказательстве, вопрос состоит лишь в оценке для конкретной функции величины , которая называется остаточным членом в формуле Тейлора. Применение формулы Тейлора разумно в том случае, когда остаточный член является малой величиной и стремится к 0 при . Для непосредственного применения формулы Тейлора необходимо вычислить производные функции в точке .

Пример 1. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Так как функция совпадает со всеми своими производными, то выполнено условие и формула (6) принимает вид . (4)

Пример 2. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Если , то , , , 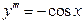и далее производные функции повторяются. Значения синуса и его производных в точке 0 соответственно равны числам: 0, 1, 0, -1, 0 и т. д. Это можно записать в виде формул: , , . Следовательно, искомая формула принимает вид . (5)

Пример 3. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Если , то , , , и далее производные функции повторяются. Значения косинуса и его производных в точке 0 соответственно равны числам: 1, 0, -1, 0, 1 и т. д. Это можно записать в виде формул: , , . Следовательно, искомая формула принимает вид . (6)

Обратите внимание, что формула (9) может быть получена из формулы (8) дифференцированием ее левой и правой частей. И это не случайно. Не обязательно каждый раз вычислять все производные исследуемой функции.

Пример 4. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Искомую формулу мы получим, заменив в формуле (7) аргумент на аргумент . Учитывая, что , мы приходим к искомой формуле . (7)

Сопоставляя формулы (4), (5), (6), (7), мы приходим к формуле Эйлера , (8) которая упоминалась в лекции 1. Полностью формула Эйлера будет доказана, когда будет установлено, что в формулах (7), (8), (9) остаточные члены с ростом стремятся к 0 при всех значениях аргумента.

Пример 5. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Если , то , , , , …, ( ). Следовательно, искомая формула принимает вид . (9)

Оценка остаточного члена в формуле Тейлора

Неотъемлемой частью использования формулы Тейлора является оценка ее остаточного члена. Красивые и практичные формулы появлялись в работах выдающихся математиков 18, 19 и да в 20 веках. Отметим некоторые результаты без доказательства.

Теорема 1. (Теорема Лагранжа) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда для произвольной точки из этой окрестности найдется точка , принадлежащая интервалу, соединяющую точки и , обладающую тем свойством, что в формуле (5) выполнено соотношение , (10)

Теорема 2. (Теорема Коши) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда для произвольной точки из этой окрестности найдется точка , принадлежащая интервалу, соединяющую точки и , обладающую тем свойством, что в формуле (5) выполнено соотношение , (11)

Теорема 3. (Теорема Пеано) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда в формуле (5) выполнено соотношение , (12)