Условия возрастания и убывания функции
Функция 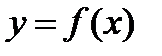 , определенная на сегменте (или интервале), называется возрастающей на этом сегменте (интервале), если из неравенства
, определенная на сегменте (или интервале), называется возрастающей на этом сегменте (интервале), если из неравенства
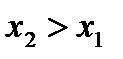 ,
, 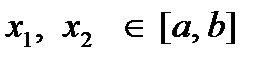 (
( 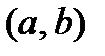 ),
),
следует, что
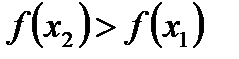 .
.
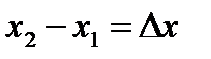 ,
,  ,
,
 и
и 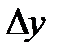 имеют одинаковые знаки, следовательно,
имеют одинаковые знаки, следовательно, 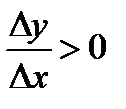 .
.
Функция 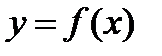 , определенная на сегменте
, определенная на сегменте  (или интервале
(или интервале 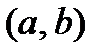 ), называется убывающей на этом сегменте (интервале), если из неравенства
), называется убывающей на этом сегменте (интервале), если из неравенства
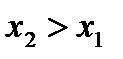 ,
,  (
( 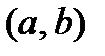 ),
),
следует, что
 .
.
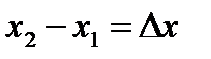 ,
,  ,
,
 и
и 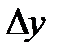 имеют разные знаки, следовательно,
имеют разные знаки, следовательно,  .
.
Теорема 1.1. Если 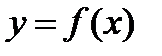 , имеющая производную на
, имеющая производную на  , возрастает, то
, возрастает, то  (не отрицательна) на
(не отрицательна) на  .
.
1.2. Если 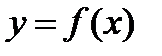 непрерывна и дифференцируема в
непрерывна и дифференцируема в 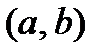 , причем
, причем  ,
, 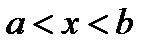 , то
, то 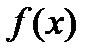 возрастает на
возрастает на  .
.
Доказательство.
1) 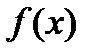 возрастает на
возрастает на  , придадим
, придадим 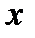 приращение
приращение  и рассмотрим
и рассмотрим
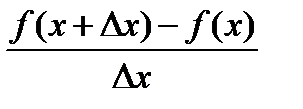 . (1)
. (1)
Так как 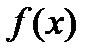 возрастает, то
возрастает, то 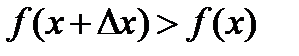 при
при 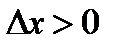 и
и 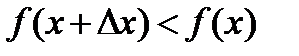 при
при 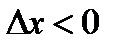 . Но формула (1) > 0 , следовательно,
. Но формула (1) > 0 , следовательно,
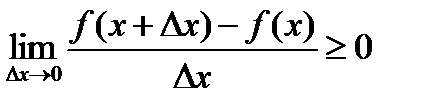 ,
,
то есть  , что и требовалось доказать.
, что и требовалось доказать.
2) Пусть 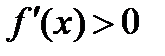 при любом
при любом 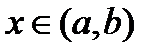 . Рассмотрим
. Рассмотрим 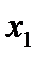 и
и 
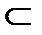
 .
. 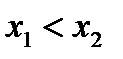 по теореме Лагранжа о конечных приращениях.
по теореме Лагранжа о конечных приращениях.
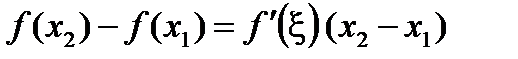 ,
, 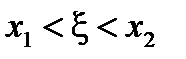 .
.
Так как 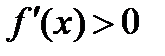 , то
, то  ,
, 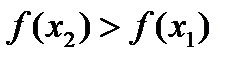 – возрастает.
– возрастает.
Теорема 2.1. Если 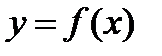 убывает на
убывает на  , то
, то  .
.
2.2. Если  в
в 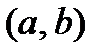 , то
, то 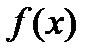 убывает на отрезке
убывает на отрезке  (
( 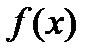 непрерывна и дифференцируема).
непрерывна и дифференцируема).
Замечание. Если на 
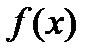 возрастает, то касательная к
возрастает, то касательная к 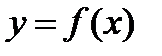 в любой точке на этом отрезке образует с
в любой точке на этом отрезке образует с 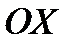 острый угол
острый угол  или в отдельных случаях горизонталь:
или в отдельных случаях горизонталь:
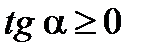 ,
, 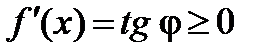 .
.
Если 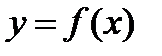 убывает, то угол тупой (или в отдельных точках касательная параллельна оси
убывает, то угол тупой (или в отдельных точках касательная параллельна оси 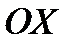 ):
):  .
.
Функция только возрастающая или только убывающая называется монотонно возрастающей или монотонно убывающей.
Пример. Определить интервалы монотонности  .
.
Решение.
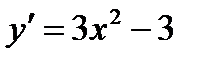 ,
,
 ,
,  ,
,
 и
и  – возрастает;
– возрастает;
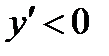 ,
, 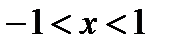 – убывает (рис. 8).
– убывает (рис. 8).
