Элементы проверки статических гипотез
Оценка закона распределения по данным выборки предполагает последовательное решение трех проблем:1) выбор типа теоретического (генерального) распределения и определение его параметров по результатам выборки; 2) построение теоретического ряда по найденному закону распределения или решение отдельных задач; 3) оценка расхождения (согласия) между теоретическим и опытным рядами.
Элементы корреляционного анализа
Линейная корреляция
Корреляционный анализ наряду с выборочным методом представляет собой важнейшее прикладное направление математической статистики. Предметом его исследования является
связь (зависимость) между различными варьирующими признаками (переменными величинами), при которой каждому значению одной переменной соответствует не определенное значение другой (как это имеет место при функциональной зависимости), а ряд распределения с определенной групповой средней.
Конечная цель корреляционного анализа –получение уравнений прямых регрессии, характеризующих форму зависимости и вычисление коэффициента корреляции, определяющего тесноту (силу) связи, если она линейная.
Расчет производится в два основных этапа. На первом –обрабатывают табличные данные для нахождения величины 
и 
.
При этом используется упрощенная схема вычисления (т.е. переход от 
и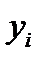 
к условным переменным 
и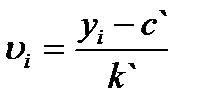 
) и применяются расчетные формулы (6.6.5-6.6.8).
Второй этап –вычисление основных параметров корреляционной зависимости (gy/x, gx/y, r) по формулам (6.6.9), (6.6.10) и оценка их достоверности.
При выполнении контрольной работы необходимо руководствоваться следующим.
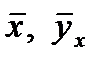Графическое изображение прямых регрессии (обе должны быть построены на одном чертеже) может служить для контроля правильности расчетов: они должны образовывать с осью ОХ либо только острые, либо только тупые углы в зависимости от знака (или r), опытные точки с координатами ( 
) и (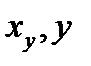 
) должны располагаться по обе стороны соответствующих прямых регрессии; прямые регрессии должны пересекаться в центре распределения ( ).
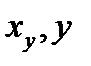Чертеж следует выполнять четко и аккуратно, удачно выбирая масштабы по каждой оси (они могут быть разными) и начала отсчетов.
Все расчеты следует вести с разумной степенью точности (как правило, сохраняя два знака после запятой в окончательных данных). Для этого в промежуточных вычислениях достаточно сохранить три знака после запятой (правило «Лишней цифры»).
Основные формулы
Упрощенный способ вычисления средних, дисперсий и величины .
Групповые средние:
, (6.6.5)
где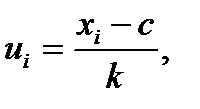 
,
а c, k, c`, k` -произвольные числа.
Общие средние и дисперсии:
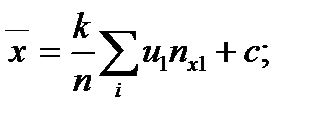
; (6.6.6)
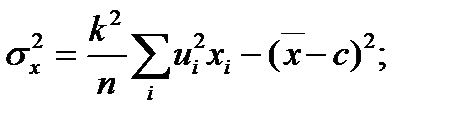
. (6.6.7)
Ковариация
. (6.6.8)
Коэффициенты регрессий и корреляций
; 
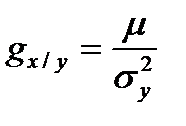(6.6.9)
. (6.6.10)
Уравнение прямых регресси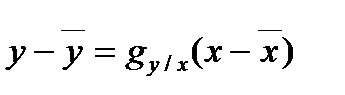й:
и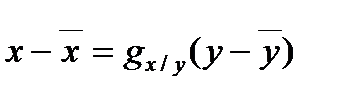 
. (6.6.11)