Направляющие косинусы вектора ускорения
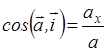 ;
; 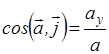 ;
; 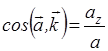 (30)
(30)
Угол между векторами и определяется из равенства
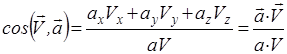 (31)
(31)
Тангенциальное ускорение точки 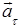 характеризует быстроту изменения вектора скорости в данный момент времени и выражается формулой (см. рис. 4)
характеризует быстроту изменения вектора скорости в данный момент времени и выражается формулой (см. рис. 4)
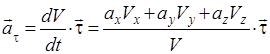 (32)
(32)
где 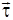 – единичный вектор касательной. Очевидно, имеет место также равенство
– единичный вектор касательной. Очевидно, имеет место также равенство
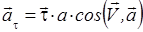 (33)
(33)
Если 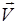 возрастает с течением времени, то
возрастает с течением времени, то 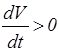 и
и 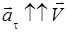 , т.е.
, т.е. 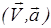 – острый угол. Если
– острый угол. Если 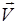 убывает, то
убывает, то 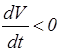 и
и 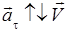 , т. е
, т. е 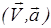 – тупой угол (рис. 4).
– тупой угол (рис. 4).
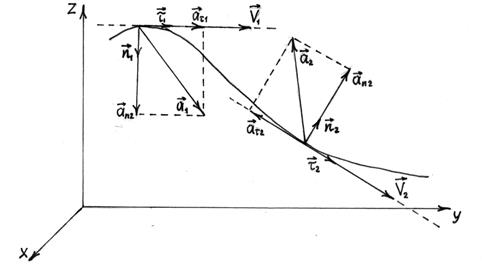
Рисунок 4 – Вектор тангенциального и нормального ускорений
Нормальное ускорение 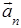 характеризует быстроту изменения в данный момент направления вектора
характеризует быстроту изменения в данный момент направления вектора 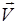 и выражается формулой:
и выражается формулой:
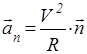 , (34)
, (34)
где 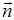 – единичный вектор нормали к траектории, направленный в сторону вогнутости траектории
– единичный вектор нормали к траектории, направленный в сторону вогнутости траектории 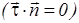 . R – радиус кривизны траектории, представляющий собой радиус соприкасающейся с траекторией в данной точке окружности, совпадающей с бесконечно малым элементом траектории с точностью до бесконечно малых величин второго порядка малости.
. R – радиус кривизны траектории, представляющий собой радиус соприкасающейся с траекторией в данной точке окружности, совпадающей с бесконечно малым элементом траектории с точностью до бесконечно малых величин второго порядка малости.
Полное ускорение можно записать в виде
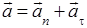 и
и 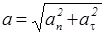 (35)
(35)
Если движутся две частицы, то важной величиной является так называемая относительная скорость частиц. Скоростью частицы 2 относительно частицы 1 называется скорость частицы 2 в системе отсчета, в которой частица 1 покоится. 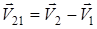 . Еще одной величиной, характеризующей относительное движение частиц, является скорость сближения (удаления) частиц – это скорость изменения расстояния между частицами:
. Еще одной величиной, характеризующей относительное движение частиц, является скорость сближения (удаления) частиц – это скорость изменения расстояния между частицами:
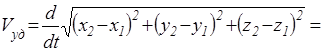
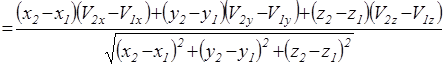 (36)
(36)
Можно показать, что скорость удаления Vуд > 0 или сближения Vуд < 0 можно найти по очевидной формуле:
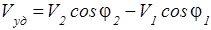 ,
,
где смысл обозначений ясен из следующего рисунка
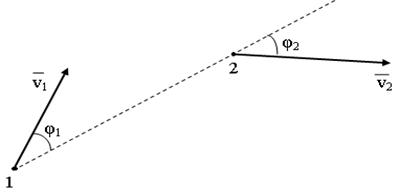
Рисунок 5 – Скорость сближения (удаления) двух частиц
Удобным способом нахождения всех кинематических характеристик движения точки является способ, основанный на использовании стробоскопических фотографий движущейся точки. Стробоскопические фотографии получаются, если движущуюся точку фотографировать на один и тот же кадр через строго фиксированные промежутки времени, называемые периодом стробоскопирования τ. Время открытия затвора при этом должно быть малым для того, чтобы за это время фотографируемая точка заметно не сдвинулась и её изображение не смазалось. Применяется также вариант фотографирования в темноте с открытым затвором, когда движущийся объект освещается короткими мощными импульсами света, следующими друг за другом за время τ. На фотографиях обычно указывается масштаб расстояний и период стробоскопирования τ. Если движение точки происходит по пространственной кривой, то лучше как минимум две фотографии, снятые фотоаппаратами с разных позиций. Если движение происходит в плоскости, то фотоаппарат располагают так, чтобы плоскость плёнки была параллельна этой плоскости. Можно считать при этом, что на фотографии в неискажённом виде в некотором масштабе получается картина движения точки. На фотографии нужно также указать направление движения точки.
В работе стробоскопические фотографии имитируются с помощью прозрачных плёнок с пробитыми в них отверстиями, которые накладываются на двойной лист бумаги, и затем с помощью ручки, картина переносится на лист бумаги. Траекториями движения частиц во всех вариантах являются параболы. Период стробоскопирования равен 0,1 секунды (напомним, это означает, что
τ = (0,100  0,005) секунд). Масштабный фактор равен 1, т.е. все расстояния можно определять непосредственно по рисунку. Для описания движения нужно выбрать систему координат. Напомним, что начало координат следует выбирать так, чтобы не было близких к нулю значений координат, а расположение осей соответствовало бы одному из четырех рисунков (по указанию преподавателя).
0,005) секунд). Масштабный фактор равен 1, т.е. все расстояния можно определять непосредственно по рисунку. Для описания движения нужно выбрать систему координат. Напомним, что начало координат следует выбирать так, чтобы не было близких к нулю значений координат, а расположение осей соответствовало бы одному из четырех рисунков (по указанию преподавателя).
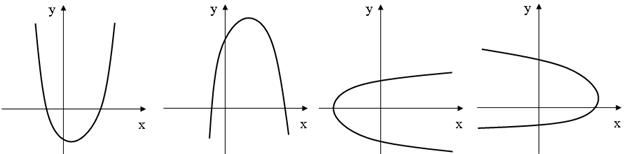
На каждом из рисунков возможны два варианта движения: против часовой стрелки или по часовой стрелке (по указанию преподавателя).
