Исходные данные к индивидуальным работам

В качестве исходных данных используются ряды среднемесячной температуре поверхности в разных точках акватории Атлантического океана с 1957 по 1993 гг.

В каждый вариант исходных данных включены 3 временных ряда. Для выполнения индивидуальных работ нужно исследовать или все три ряда, или один из них, что указано в каждом конкретном задании.

Таблица 1.

Варианты выбора исходных данных

Варианты	Точки	Месяцы
		1, 2, 3
		4, 5, 6
		7, 8, 9
		10, 11, 12
		1, 2, 3
		4, 5, 6
		7, 8, 9
		10, 11, 12
		1, 2, 3
		4, 5, 6
		7, 8, 9
		10, 11, 12
		1, 2, 3
		4, 5, 6
		7, 8, 9
		10, 11, 12
		1, 2, 3
		4, 5, 6

Таблица 2.

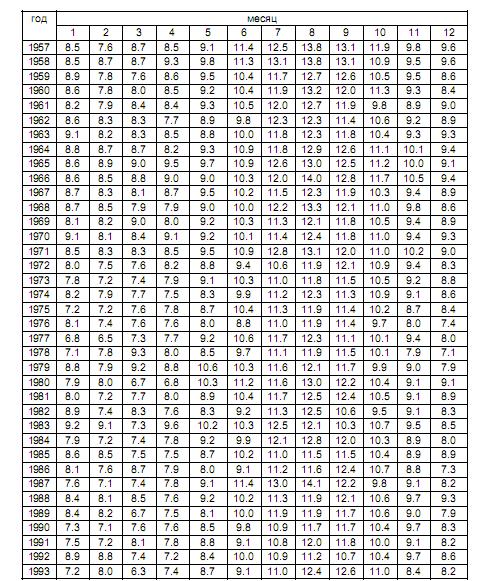
Температура поверхности океана (^оС) в точке 3 (60^о с.ш. 30^о з.д.)

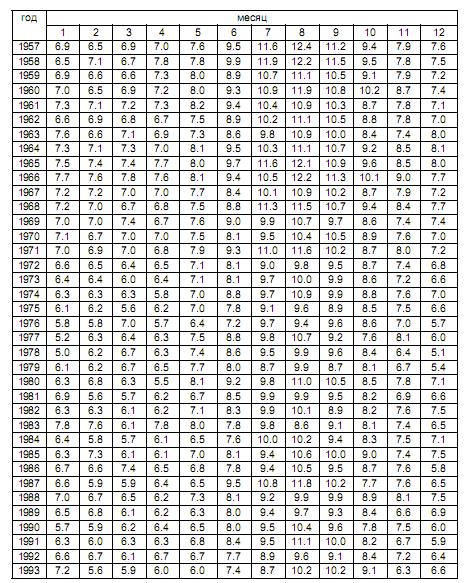
Температура поверхности океана (^оС) в точке 4 (60^о с.ш. 20^о з.д.)

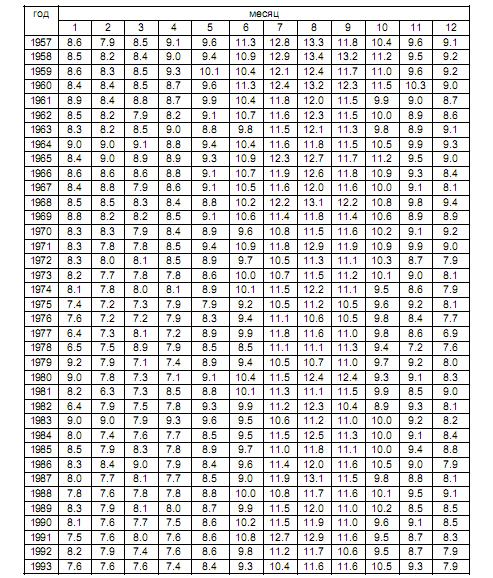
Температура поверхности океана (^оС) в точке 7 (55^о с.ш. 50^о з.д.)

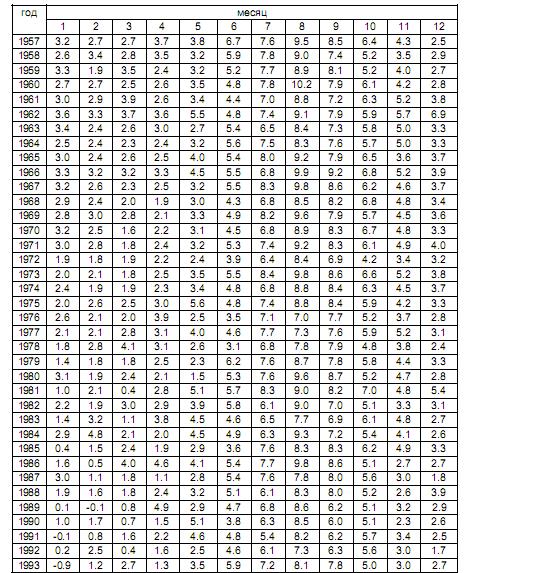
Температура поверхности океана (^оС) в точке 8 (55^о с.ш. 40^о з.д.)

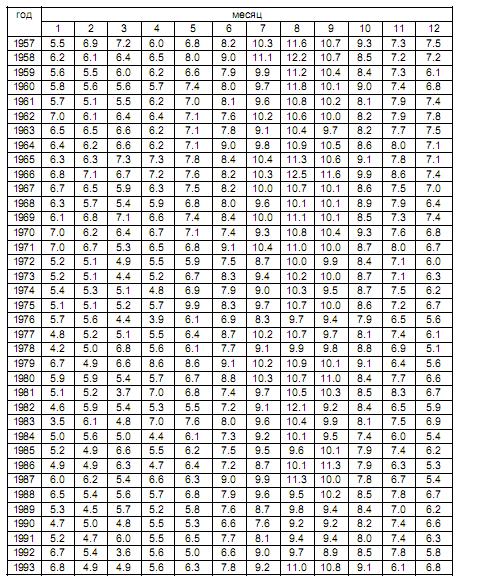
Температура поверхности океана (^оС) в точке 9 (55^о с.ш. 30^о з.д.)

Приложение 2

ОСНОВНЫЕ СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ

Таблица 1.

Значения функции Лапласа Ф₀(z) =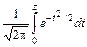

z
0,0	0,000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0,341
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0	0,477
2,1
2,2
2,3
2,4
2,5
2.6
2.7
2,8
2,9

3,0	0,49865	3,1	0,49903	3,2	0,49931	3,3	0,49952
3,4	0.49966	3,5	0,49977	3,6	0,49984	3,7	0,49989
3,8	0,49993	3,9	0.49995	4,0	0,499968	5,0	0,4999999

Таблица 2.

Критические значения t-критерия Стьюдента

при заданном уровне значимости a и степени свободы k­

t_кр = t_кр(k, a)

k	Уровень значимости a (двусторонняя критическая область)
0,1	0,05	0,02	0,01	0,005	0,002	0,001
	6,314	12,706	31,821	63,657	127,321	318,309	636,619
	2,920	4,303	6,965	9,925	14,089	22,327	31,599
	2,353	3,182	4,541	5,841	7,453	10,214	12,924
	2,132	2,776	3,747	4,604	5,597	7,173	8,610
	2,015	2,571	3,365	4,032	4,773	5,893	6,869
	1,943	2,447	3,143	3,707	4,317	5,208	5,959
	1,895	2,365	2,998	3,499	4,029	4,785	5,408
	1,860	2,306	2,896	3,355	3,833	4,501	5,041
	1,833	2,262	2,821	3,250	3,690	4,297	4,781
	1,812	2,228	2,764	3,169	3,581	4,144	4,587
	1,796	2,201	2,718	3,106	3,497	4,025	4,437
	1,782	2,179	2,681	3,055	3,428	3,930	4,318
	1,771	2,160	2,650	3,012	3,372	3,852	4,221
	1,761	2,145	2,624	2,977	3,326	3,787	4,140
	1,763	2,131	2,602	2,947	3,286	3,733	4,073
	1,746	2,120	2,583	2,921	3,252	3,686	4,015
	1,740	2,110	2,567	2,898	3,222	3,645	3,985
	1,734	2,101	2,552	2,878	3,197	3,610	3,922
	1,729	2,093	2,540	2,861	3,174	3,579	3,883
	1,725	22,086	2,528	2,845	3,153	3,552	3,849
	1,717	2,074	2,508	2,819	3,119	3,505	3,792
	1,711	2,064	2,492	2,797	3,091	3,467	3,745
	1,706	2,056	2,479	2,779	3,067	3,435	3,707
	1,701	2,048	2,467	2,763	3,047	3,408	3,674
	1,697	2,042	2,457	2,750	3,030	3,385	3,646
	1,690	2,030	2,440	2,720	2,996	3,340	3,591
	1,688	2,028	2,434	2,719	2,990	3,333	3,582
	1,684	2,021	2,423	2,704	2,971	3,307	3,551
	1,676	2,009	2,403	2,678	2,937	3,261	3,496
	1,660	1,984	2,364	2,626	2,871	3,174	3,390
¥	1,645	1,960	2,326	2,576	2,807	3,090	3,291

Таблица 3.

Критические значения χ2 – распределения

С k степенями свободы

при разных уровнях значимости a = 1 – g

	a
k	0,01	0,02	0,025	0,05	0,95	0,98	0,99
	6,635	5,412	5,024	3,841	0,004	0,001	0,000
	9,210	7,824	7,378	5,991	0,103	0,040	0,020
	11,345	9,837	9,348	7,815	0,352	0,185	0,115
	13,277	11,668	11,143	9,488	0,711	0,429	0,297
	15,086	13,388	12,833	11,070	1,145	0,752	0,554
	16,812	15,033	14,449	12,592	1,635	1,134	0,872
	18,475	16,622	16,013	14,067	2,167	1,564	1,239
	20,090	18,168	17,535	15,507	2,733	2,032	1,646
	21,666	19,679	19,023	16,919	3,325	2,532	2,088
	23,209	21,161	20,483	18,307	3,940	3,059	2,558
	24,725	22,618	21,920	19,675	4,575	3,609	3,053
	26,217	24,054	23,337	21,026	5,226	4,178	3,571
	27,688	25,472	24,736	22,362	5,892	4,765	4,107
	29,141	26,873	26,119	23,685	6,571	5,368	4,660
	30,578	28,259	27,488	24,996	7,261	5,985	5,229
	32,000	29,633	28,845	26,296	7,962	6,614	5,812
	33,409	30,995	30,191	27,587	8,672	7,255	6,408
	34,805	32,346	31,526	28,869	9,390	7,906	7,015
	36,191	33,687	32,852	30,144	10,117	8,567	7,633
	37,566	35,020	34,170	31,410	10,851	9,237	8,260
	38,932	36,343	35,479	32,671	11,591	9,915	8,897
	40,289	37,659	36,781	33,924	12,338	10,600	9,542
	41,638	38,968	38,076	35,172	13,091	11,293	10,196
	42,980	40,270	39,364	36,415	13,848	11,992	10,856
	44,314	41,566	40,646	37,652	14,611	12,697	11,524
	45,642	42,856	41,923	38,885	15,379	13,409	12,198
	46,963	44,140	43,195	40,113	16,151	14,125	12,879
	48,278	45,419	44,461	41,337	16,928	14,847	13,565
	49,588	46,693	45,722	42,557	17,708	15,574	14,256
	50,892	47,962	46,979	43,773	18,493	16,306	14,953
	52,191	49,226	48,232	44,985	19,281	17,042	15,655
	53,486	50,487	49,480	46,194	20,072	17,783	16,362
	54,776	51,743	50,725	47,400	20,867	18,527	17,074

Таблица 4.

Критические значения F-критерия Фишера с k1 и k2 степенями

свободы для уровня значимости a = 0,05

k1 k2										¥
	161,5	199,5	215,7	224,6	230,2	233,9	238,9	243,9	249,0	254,3
	18,51	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,45	19,50
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,90	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,20	3,09	2,95	2,79	2,61	2,40
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,50	2,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,77	2,60	2,42	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,29	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,45	3,59	3,20	2,96	2,81	2,70	2,55	2,38	2,19	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,38	3,52	3,13	2,90	2,74	2,63	2,48	2,31	2,11	1,88
	4,35	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,08	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05	1,81
	4,30	3,44	3,05	2,82	2,66	2,55	2,40	2,23	2,03	1,78
	4,28	3,42	3,03	2,80	2,64	2,53	2,38	2,20	2,00	1,76
	4,26	3,40	3,01	2,78	2,62	2,51	2,36	2,18	1,98	1,73
	4,24	3,38	2,99	2,76	2,60	2,49	2,34	2,16	1,96	1,71
	4,22	3,37	2,98	2,74	2,59	2,47	2,32	2,15	1,95	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,30	2,13	1,93	1,67
	4,20	3,34	2,95	2,71	2,56	2,44	2,29	2,12	1,91	1,65
	4,18	3,33	2,93	2,70	2,54	2,43	2,28	2,10	1,90	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,12	3,26	2,87	2,64	2,48	2,37	2,22	2,04	1,83	1,57
	4,08	3,23	2,84	2,61	2,45	2,34	2,18	2,00	1,79	1,51
	4,06	3,21	2,81	2,58	2,42	2,31	2,15	1,97	1,76	1,48
	4,03	3,18	2,79	2,56	2,40	2,29	2,13	1,95	1,74	1,44
	4,00	3,15	2,76	2,52	2,37	2,25	2,10	1,92	1,70	1,39
	3,98	3,13	2,74	2,50	2,35	2,23	2,07	1,89	1,67	1,35
	3,96	3,11	2,72	2,49	2,33	2,21	2,06	1,88	1,65	1,31
	3,95	3,10	2,71	2,47	2,32	2,20	2,04	1,86	1,64	1,28
	3,94	3,09	2,70	2,46	2,30	2,19	2,03	1,85	1,63	1,26
	3,92	3,07	2,68	2,44	2,29	2,17	2,01	1,83	1,60	1,21
	3,90	3,06	2,66	2,43	2,27	2,16	2,00	1,82	1,59	1,18
	3,89	3,04	2,65	2,42	2,26	2,14	1,98	1,80	1,57	1,14
	3,87	3,03	2,64	2,41	2,25	2,13	1,97	1,79	1,55	1,10
	3,86	3,02	2,63	2,40	2,24	2,12	1,96	1,78	1,54	1,07
	3,86	3,01	2,62	2,39	2,23	2,11	1,96	1,77	1,54	1,06
	3,85	3,00	2,61	2,38	2,22	2,10	1,95	1,76	1,53	1,03
¥	3,84	2,99	2,60	2,37	2,21	2,09	1,94	1,75	1,52

Индивидуальная работа № 1 Приложение 3.

ФИО, Вариант № ____

Задание 1. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (критерию c²)

Год

Месяц 1, Х1

Ранжиро-ванный ряд

Границы интервалов (ai, ai+1)

Середина интервалов, х(i)

Абсолютн. частота, mi

Относит. частота, wi

Границы интервалов

Ф0(zi)

Ф0(zi+1)

Pi

m'i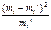

Объем выборки, n Минимальное значение, xmin Максимальное значение, xmax

ai

ai+1

zi

zi+1

Размах, R

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

Число интервалов, N

Итого

c2набл

Величина интервалов, h

Выборочное среднее,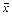

График трех температурных рядов

Гистограмма и полигон абсолютных частот

Выборочное среднеквадратическое отклонение, Sn

c2набл

Гипотеза Н0:формулировка

Число степеней свободы, k

Первый уровень значимости, a1

Вывод для уровня значимости a1: формулировка

c2кр(a1; k)

Вывод для уровня значимости a2: формулировка

Второй уровень значимости, a2

c2кр(a2; k)

ФИО, Вариант № ____

Задание 2. Основные выборочные характеристики

Год

Месяц 1, Х1

Месяц 2, Х2

Месяц 3, Х3

Абсол. частота

Абсол. накопл. частота

(Х1 ­– Хср)3

(Х2 ­– Хср)3

(Х3 ­– Хср)3

(Х1 ­– Хср)4

(Х2 ­– Хср)4

(Х3 ­– Хср)4

Y*

(Y*-Yср)2

(Y – Y*)2

m1

m2

m3

mс1

mс2

mс3

…

…

Итого

Основные статистические параметры температуры поверхности океана в ____________________________ (1957-1993 гг.) в точке _____ (55^о с.ш. 30^о з.д.)

	Месяц 1, Х1	Месяц 2, Х2	Месяц 3, Х3	Вывод		Результаты средств анализа данных пакета MS Excel
Среднее арифметическое						Месяц 1, Х1	Месяц 2, Х2	Месяц 3, Х3
Выборочная дисперсия
Выборочная исправленная дисперсия
Стандартное отклонение
Коэффициент вариации
Коэффициент асимметрии
Коэффициент эксцесса
Мода (моды)
медиана

Индивидуальная работа № 1

ФИО, Вариант № ____

Задание 3. Измерение взаимной зависимости

Задание 4. Расчет коэффициентов линейного уравнения регрессии

Задание 5. Оценка адекватности регрессионной модели

Выборочные характеристики

Sх

Sу

Sху

СТАНДОТКЛОНП для Х

СТАНДОТКЛОНП для Y

КОВАР

Уравнение модели: y*(x) = a x + b

Параметры линейной регрессии

Оценка значимости

Вывод

rxy

sr

tрасч

tкр(k; a)

ПИРСОН

СТЬЮДРАСПОБР

q

a

g

zg

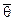b

se2

a

sa

Тa

tкр(k; a)

b

sb

Tb

tкр(k; a)

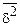F*

Fтабл(1; 35; 0,05)

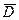h2y(x)

se

Sу

0,67Sу

Вывод

ЛИНЕЙН		Корреляционное поле		График вычисленныхy*и фактическихy значений температуры воды
a	b
…	…

Индивидуальная работа № 2

ФИО, Вариант № ____

Задание 1. Построение автокорреляционной функции

s = 1

…

s = 18

Вычисление числителя

Знаменатель

Вычисление числителя

Знаменатель

Год

yt

Скобка 1

Скобка 2

Числитель

Скобка 1

Скобка 2

Знаменатель

Скобка 1

Скобка 2

Числитель

Скобка 1

Скобка 2

Знаменатель

y1

…

y37

s

rs

График автокорреляционной функции

ФИО, Вариант № ____

Задание 2. Анализ временной изменчивости ряда температуры воды

Модель линейной регрессии связи температуры воды в ­­­­­­­­­­­­­­­­­­­__________ месяце в период с1957 по 1993 гг. в точке ____ (55^о с.ш. 30^о з.д.), ее параметры и оценка их значимости

Выборочные характеристики
Уравнение модели тренда: y*(t)= а t + b
Параметры линейной регрессии	Оценка значимости	Вывод
a
b
rty		sr		tрасч		tкр(k; a)
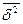						h2y(t)
se2
se		Sу		0,67Sу
Вывод

Год	Наименование месяца, yt	Медианный метод, Ме = ___	Метод серий	Скользящая средняя	Условное время, t	Значения тренда, y*	(y*– yср)2	(y – y*)2
…	…
…	…
Т = __		Число серий v(T) = ____ Длина наиб. серии l(T) = ____ Проверка неравенств: Вывод:	Число серий v(T) = ____ Длина наиб. серии l(T) = ____ Проверка неравенств: Вывод:	Вывод по графику:

График исходного и сглаженного ряда

График тренда и исходного временного ряда

Приложение 4.