Пояснения по выполнению контрольной работы
Контрольная работа
Контрольная работа состоит из двух составных частей: теоретической и практической.
Теоретическая часть включает в себя вопросы, приведенные ниже.
1 вариант - опишите предмет и методы эконометрики.
2 вариант - раскройте сущность парной регрессии.
3 вариант - оценка параметров линейной парной регрессии.
4 вариант - проверка качества уравнения парной регрессии. F-критерий Фишера.
5 вариант - точность коэффициентов парной регрессии. Проверка значимости.
6 вариант - охарактеризуйте понятие множественной регрессии.
7 вариант - оценка параметров уравнения линейной множественной регрессии.
8 вариант - проверка качества уравнения множественной регрессии. F-критерий Фишера.
9 вариант - точность коэффициентов множественной регрессии. Доверительные интервалы.
10 вариант - понятие временных рядов, его составляющие.
Практическая часть предусматривает решение двух задач по темам: «Парная регрессия» и «Временные ряды в эконометрических исследованиях».
Номер варианта контрольной работы определяется по последней цифре зачетной книжки.
Задачи контрольной работы по дисциплине «Эконометрика»
Задача 1
По 12 предприятиям концерна изучается зависимость прибыли (тыс. руб.) у от выработки продукции на 1 человека (единиц) х по следующим данным (таблица 3):
Таблица 3 - Зависимость прибыли (тыс. руб.) от выработки продукции на 1 чел.
| Номер предприятия | Выработка продукции на одного человека, ед., х | Прибыль предприятия, тыс. руб., у | ||||||||||||
| Варианты | Варианты | |||||||||||||
| № предприятия | Выработка продукции на одного человека, ед., х | Прибыль предприятия, тыс. руб., у | ||||||||||||
| Варианты | Варианты | |||||||||||||
| № предприятия | Выработка продукции на одного человека, ед., х | Прибыль предприятия, тыс. руб., у | ||||||||||||
| Варианты | Варианты | |||||||||||||
1. Построить линейное уравнение парной регрессии ŷ=f(х).
2. Рассчитать линейные коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Дать точечный и интервальный прогноз прибыли с вероятностью 0,95, принимая уровень выработки равным 92 единицам.
Задача 2
По исходным данным, характеризующим динамику потребления овощей по области за определенный период времени на одного члена семьи, необходимо:
1. Установить форму модели и записать ее в общем виде исходя из графических построений и трехэлементных скользящих средних.
2. Рассчитать параметры модели, используя метод наименьших квадратов (МНК).
3. Оценить правильность выбора модели с помощью F-критерия Фишера и статистическую значимость параметров по t-критерию Стьюдента.
4. Определить прогнозный уровень потребления овощей по области с упреждением на 3 временных отрезка (l=3) и построить доверительные интервалы.
Таблица 4 - Исходные данные
| Временные отрезки области исследования, t | Объемы потребления овощей по области на одного члена семьи, кг, уt | |||||||||
| Варианты | ||||||||||
| 10,0 | 10,2 | 10,4 | 10,6 | 10,8 | 11,0 | 11,2 | 11,4 | 11,6 | 11,8 | |
| 10,7 | 10,9 | 11,1 | 11,3 | 11,5 | 11,7 | 11,9 | 12,1 | 12,3 | 12,5 | |
| 12,0 | 12,2 | 12,4 | 12,6 | 12,8 | 13,0 | 13,2 | 13,4 | 13,6 | 13,8 | |
| 10,3 | 10,5 | 10,7 | 10,9 | 11,1 | 11,3 | 11,5 | 11,7 | 11,9 | 12,1 | |
| 12,9 | 13,1 | 13,3 | 13,5 | 13,7 | 13,9 | 14,1 | 14,3 | 14,5 | 14,7 | |
| 16,3 | 16,5 | 16,7 | 16,9 | 17,1 | 17,3 | 17,5 | 17,7 | 17,9 | 18,1 | |
| 15,6 | 15,8 | 16,0 | 16,2 | 16,4 | 16,6 | 16,8 | 17,0 | 17,2 | 17,4 | |
| 17,8 | 18,0 | 18,2 | 18,4 | 18,6 | 18,8 | 19,0 | 19,2 | 19,4 | 19,6 | |
| 18,0 | 18,2 | 18,4 | 18,6 | 18,8 | 19,0 | 19,2 | 19,4 | 19,6 | 19,8 |
Пояснения по выполнению контрольной работы
При решении задачи 1 необходимо руководствоваться следующим алгоритмом решения, приведенным ниже.
Для нахождения параметров а и b парной линейной регрессии у=а+bх используют метод наименьших квадратов (МНК), который заключается в решении системы нормальных уравнений относительно а и b:
 (1)
(1)
Для нахождения параметров а и b необходимо воспользоваться следующими формулами:
b=  , (2) где
, (2) где  =
= 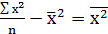 -
-  (3)
(3)
a=ӯ-b 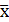 . (4)
. (4)
А также произвести вспомогательные расчеты в таблице 5.
Таблица 5 – Вспомогательные расчеты
| № предприятия | х | у | х∙у | х2 | у2 |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | |
| ∑ | ? | ? | ? | ? | ? |
| Среднее значение | ? | ? | ? | ? | ? |
Уравнение регрессии всегда дополняется расчетом показателя тесноты связи. В линейных регрессиях в качестве такого показателя выступает линейный коэффициент корреляции, который рассчитывается по формуле:
 =b
=b  =
= 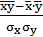 , (5)
, (5)
где 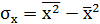 , σy=
, σy=  . (6)
. (6)
Если коэффициент регрессии b  0, то 0≤
0, то 0≤  ≤1, и, наоборот, при b<0 -1≤
≤1, и, наоборот, при b<0 -1≤  ≤0.
≤0.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции, который называется коэффициентом детерминации, характеризующим долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака.
Чем больше доля объясненной вариации, тем меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные. И соответственно ею можно воспользоваться для прогноза значений результативного признака. Чем ближе коэффициент детерминации к 1, тем в большей степени уравнение регрессии пригодно для прогнозирования.
Для того, чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую:
 =
= 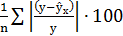 . (7)
. (7)
Ошибка аппроксимации, находящаяся в пределах 5-7 %, свидетельствует о хорошем подборе модели к исходным данным.
В линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров.
Для этого по каждому из параметров определяется его стандартная ошибка, а также и для коэффициента корреляции: sa и sb, sr.
Стандартные ошибки коэффициентов регрессии (sa, sb) и коэффициента корреляции sr определяются соотношениями:
sb= 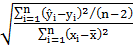 =
= 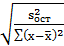 =
= 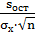 . (8)
. (8)
sa= 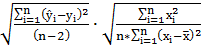 =
=  =sост
=sост  , (9)
, (9)
где s2ост - несмещенная оценка остаточной дисперсии.
s2ост=  . (10)
. (10)
sr= 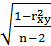 . (11)
. (11)
Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику при (n-2) степенях свободы, которую используют для проверки статистической значимости коэффициента регрессии и для расчета его доверительных интервалов.
Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, таким образом, определяя расчетное значение t-критерия Стьюдента:
ta=  , (12)
, (12)
tb=  , (13)
, (13)
tr=  , (14)
, (14)
которое затем сравнивают с табличным значением (приложение Б) при определенном уровне значимости α и числе степеней свободы df=n-2.
Для расчета доверительных интервалов для параметров а и b необходимо определить предельную ошибку для каждого параметра:
Δа=tт∙sa, Δb= tт∙sb. (15)
Доверительные интервалы имеют вид:
γa=a 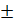 Δa, (16)
Δa, (16)
γb=b 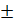 Δb. (17)
Δb. (17)
Анализ верхних и нижних границ доверительного интервала позволяет сделать вывод о том, что с вероятностью р=1-α параметры и b принимают или не принимают нулевых значений, и, соответственно, не являются или являются статистически незначимыми.
Полученные оценки уравнения регрессии используются для его прогноза.
Подставляя прогнозное значение в полученное уравнение регрессии, находим точечный прогноз.
Чтобы получить интервальный прогноз, необходимо рассчитать стандартную ошибку предсказываемого значения исследуемого показателя myp:
myp=Sост 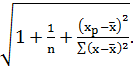 (18)
(18)
Предельная ошибка прогнозируемой величины рассчитывается как
Δур=tа∙myp. (19)
Доверительный интервал прогнозируемой величины составит
ур=ур 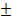 Δур. (20)
Δур. (20)
При решении задачи 2 необходимо производить расчеты в следующей последовательности.
Первоначально по элементам динамического ряда строится график для исследования характера варьирования показателя во времени.
Если графическое построение не дает возможности однозначно установить закономерность изменения признака, то на следующем этапе расчетов применяют различные статистические методы обработки данных (сглаживание по скользящей средней, определение последовательных разностей и др.), позволяющие упростить конфигурацию исходной кривой.
Цель сглаживания временного ряда заключается в получении ряда с меньшим разбросом уровней, что в ряде случаев позволяет на основе визуального анализа сделать вывод о наличии тенденции, ее характерных особенностях и модели развития явления
Сглаживание временного ряда по методу простой скользящей средней заключается в замене исходных уровней ряда yt сглаженными значениями y′t, которые получаются как среднее значение определенного числа уровней исходного ряда, симметрично окружающих значение yt.
В результате получается временной ряд y′t, меньше подверженный колебаниям.
Для вычисления сглаженных значений y′t по методу простой скользящей средней используются следующие формулы:
1. Нечетный интервал сглаживания (интервал сглаживания - количество исходных уровней ряда (yt), используемых для сглаживания):
 =
=  =
= 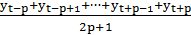 , (21)
, (21)
где уt - фактическое значение уровня исходного ряда в момент t;
y′t - значение скользящей средней в момент t;
(2р+1) - длина интервала сглаживания.
Формула (20) при интервалах сглаживания, равных трем и пяти соответственно, принимает вид:
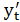 =
= 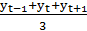 , (22)
, (22)
 =
= 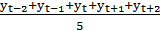 . (23)
. (23)
2. Четный интервал сглаживания:
 =
= 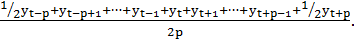 (24)
(24)
Для задачи 2 необходимо использовать трехлетние скользящие средние.
Результаты расчета сводим в таблицу 6.
Таблица 6 - Результаты расчета трехлетних скользящих средних
| Временные отрезки области исследования, t | Потребление овощей по области, yt | Скользящие трехлетние суммы, ∑уt | Скользящие трехлетние средние |
| ? | - | - | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | ? | ? | |
| ? | - | - |
Затем строится график анализируемого показателя на основании рассчитанных значений трехлетних скользящих средних (по оси ординат отмечаем временные промежутки, по оси абсцисс – анализируемый показатель).
Далее, исходя из теоретических соображений, выявляется форма зависимости анализируемого показателя и общий вид модели – тренд (ŷt=f(t)).
Для расчета параметров выбранного вида модели воспользуемся методом наименьших квадратов, суть которого заключается в построении и решении системы нормальных уравнений.
Система нормальных уравнений имеет вид:
 (25)
(25)
Чтобы решить данную систему производятся вспомогательные расчеты в таблице 7.
Таблица 7 – Вспомогательные расчеты
| t | yt | yt∙t | t2 | ŷt | |
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ? | ? | ? | ? | ||
| ∑ | ? | ? | ? | ? | ? |
Для оценки правильности выбора аналитической зависимости используется показатель F-критерий Фишера, основанный на применении методов дисперсионного анализа, позволяющих установить связь между явлениями по результатам изучения их вариации.
Расчетное значение F-критерия Фишера определяется по следующей формуле:
Fр=Dt2/Dост2, (26)
где Dt2 – факториальная дисперсия, измеряющая вариацию зависимой переменной уt за счет изменения t;
Dост2 – остаточная дисперсия, характеризующая отклонения между исходными и расчетными значениями переменной уt;
где Dt2= 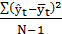 , (27)
, (27)
Dост2=  , (28)
, (28)
где 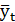 – среднее арифметическое значение признака;
– среднее арифметическое значение признака;
N – число параметров выбранной модели;
n – число временных отрезков исследования;
(N-1), (n-N) – число степеней свободы.
Для вычисления F-критерия произведем вспомогательные расчеты, которые сведем в таблицу 8.
Таблица 8 – Вспомогательные расчеты
| t | yt | ŷt |  | (yt-ŷt) |  | 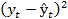 | 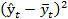 |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ? | ? | ? | ? | ? | ? | ? | |
| ∑ | - | - | - | - | - | ? | ? |
Примечание - ӯt – средняя арифметическая простая, которая рассчитывается по формуле: ӯt=  |
Правильность выбора уравнения тренда определяется путем сравнения F-критерия Фишера с табличными значениями данного показателя (приложение А). Табличное значение критерия устанавливается для k1=N-1 и k2=n-N степеней свободы. Если расчетное значение показателя окажется больше табличного (Fp>Fт), то уравнение тренда можно использовать для описания тенденции. Если же Fp<Fт, то вывод о применимости уравнения регрессии следует считать необоснованным.
Для определения статистической значимости параметров уравнения тренда необходимо рассчитать доверительную зону выборочной линии регрессии.
В связи с этим следует оценить значимость параметров а0 и a1, определив их случайные ошибки. Случайные ошибки параметров (а0 и а1) определяются по формулам:
 =Dост
=Dост 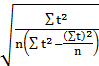 , (29)
, (29)
 =
=  , (30)
, (30)
Dост= 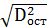 . (31)
. (31)
Для того, чтобы установить, насколько велики расхождения между параметрами уравнений, а также оценки статистической значимости параметров выбранной модели, рассчитываем t-критерий Стьюдента.
Расчетные значения t-критерия определяется для каждого параметра:
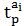 =
= 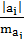 , (32)
, (32)
где 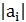 – i-е параметры модели;
– i-е параметры модели;
 – случайные ошибки i-х параметров.
– случайные ошибки i-х параметров.
Расчетные значения tр сопоставляются с соответствующими табличными величинами tт (приложение Б), найденными для k=n-2 степеней свободы и принятой доверительной вероятности 0,95 либо 0,99 (для задачи 2 использовать 0,99; т. е. α=0,01). Если tр> tт, то параметры уравнения регрессии считаются статистически значимыми и могут применяться для отображения тенденции переменной у. Если же tр< tт, то возможность несовпадения закономерностей весьма велика.
Для того, чтобы построить доверительную зону исследуемого показателя в графической форме, необходимо для каждого значения t определить ординаты точек на верхних и нижних граничных кривых (уtв, уtн), после чего точки соединяются плавными линиями.
ŷtв(н)=ŷt 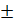 Δt, (33)
Δt, (33)
где ŷtв(н) – соответственно ординаты на верхних и нижних граничных кривых доверительной зоны;
ŷt – расчетное значение признака при вариации аргумента в рамках области исследования;
Δt – доверительные интервалы, которые определяются по следующей формуле
Δt=tт∙Dост 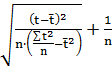 , (34)
, (34)
где tт – табличное значение t-критерия Стьюдента.
Расчет ординат точек, расположенных на верхних и нижних граничных кривых, выполним в таблице 9.
Таблица 9 - Расчет ординат точек, расположенных на верхних и нижних граничных кривых
| t | ŷt | Δtt | ytв | уtн |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ? |
На основании расчетов строится линия регрессии (ŷt=а0+а1t) и доверительная зона линии регрессии.
Доверительные интервалы для индивидуальных значений признака определяются по следующим соотношениям, предварительно рассчитав на указанный момент времени  и ∑t2:
и ∑t2:
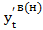 = ŷt
= ŷt 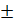 Δ′t, (35)
Δ′t, (35)
где Δ′t= tт∙Dост 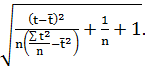 (36)
(36)
10 Вопросы для подготовки к экзамену
1. Предмет и методы эконометрики.
2. Характеристика взаимосвязей.
3. Основные этапы построения эконометрической модели.
4. Выбор вида эконометрической модели.
5. Методы отбора факторов.
6. Оценка параметров моделей.
7. Примеры эконометрических моделей.
8. Понятие парной регрессии.
9. Построение уравнения парной регрессии.
10. Оценка параметров линейной парной регрессии.
11. Проверка качества уравнения парной регрессии. F-критерий Фишера.
12. Коэффициенты корреляции парной регрессии. Оценка тесноты связи.
13. Точность коэффициентов парной регрессии. Проверка значимости.
14. Точечный и интервальный прогноз по уравнению парной линейной регрессии.
15. Коэффициент эластичности.
16. Понятие множественной регрессии.
17. Отбор факторов при построении множественной регрессии.
18. Выбор формы уравнения множественной регрессии.
19. Оценка параметров уравнения линейной множественной регрессии.
20. Проверка качества уравнения множественной регрессии.
F-критерий Фишера.
21. Точность коэффициентов множественной регрессии. Доверительные интервалы.
22. Понятие регрессионных моделей с неоднородными данными.
23. Необходимость использования в регрессионных моделях фиктивных переменных.
24. Сущность теста Чоу.
25. Проблемы построения регрессионных моделей.
26. Понятие временных рядов.
27. Составляющие временного ряда.
28. Автокорреляция уровней временного ряда.
29. Моделирование тенденции временного ряда.
30. Выбор вида тенденции.
31. Оценка адекватности и точности модели тенденции.
32. Структурная и приведенная формы модели.
33. Оценка параметров структурной формы модели.
34. Проблема идентификации.
35. Косвенный метод наименьших квадратов (МНК).
36. Двухшаговый МНК.
37. Трехшаговый МНК.
38. Применение систем эконометрических уравнений в исследованиях.
39. Предпосылки МНК.
40. Обобщенный МНК.
41. Гетероскедастичность. Гомоскедастичность.
42. Мультиколлинеарность.
43. Частная корреляция.
Список литературы
1. Агапов П.В., Афанасьев В.В., Качура Г.Н. Социальное прогнозирование: учеб. пособие. – М.: Канон РООН «Реабилитация», 2009. – 272 с.
2. Прикладная статистика. Основы эконометрики: Т. 1: Теория вероятностей и прикладная статистика. Учебник для вузов : В 2 т. / С. А. Айвазян [и др.]. – 2-е изд., испр. – М.: ЮНИТИ, 2001. - 656 с.
3. Берндт Э. Р. Практика эконометрики: классика и современность: учебник – М.: ЮНИТИ–ДАНА, 2005. – 863 с.
4. Бородич С.А. Эконометрика: учеб. пособие. – Мн.: Новое знание, 2001. - 403 с.
5. Валентинов В.А. Эконометрика: учебник. – М.: Дашков и К◦, 2008. – 435 с.
6. Доугерти К. Введение в эконометрику/ Пер. с англ. – М.: ИНФРА–М, 2009. – 456 с.
7. Замков О.О. Эконометрические методы в макроэкономическом анализе: курс лекций. – М.: ГУ ВШЭ, 2001. – 122 с.
8. Елисеева И.И. Эконометрика: учебник /Под ред. И.И. Елисеевой. – М.: Проспект, 2011. – 288 с.
9. Елисеева И.И. Практикум по эконометрике: учеб. пособие /Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2008. – 191с.
10. Кремер Н.Ш., Путко В.А. Эконометрика: учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2007. – 311 с.
11. Магнус Я.Р., Катышев П. К., Пересецкий А.А. Эконометрика: Начальный курс: учебник – 8-е изд. – М.: Дело, 2007. – 503 с.
12. Нименьях Н.Н. Эконометрика. – СПб.: Издательский дом «Нева», 2003. – 204 с.
13. Орлов А.И. Эконометрика: учеб. пособие для вузов – М.: Экзамен, 2002. - 576 с.
14. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: учебник для вузов /Рос. экон. акад. имени Плеханова Г. В., – 2-е изд., стер. – М.: Экзамен, 2007. – 510 с.
Приложение А
(справочное)
Таблица А1 - Значения F-критерия Фишера (Fт) для уровня значимости α=0,05
| Число степеней свободы | ||||||||||
| k2 | k 1 | |||||||||
| ∞ | ||||||||||
| 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | 238,9 | 243,9 | 249,0 | 254,3 | |
| 18,5 | 19,0 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,5 | 19,4 | |
| 10,1 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8,85 | 8,81 | 8,79 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | 4,74 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,26 | 4,21 | 4,15 | 4,10 | 4,06 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,69 | 3,64 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,35 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,14 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,98 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,85 | |
| 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | 2,75 | |
| 4,67 | 3,81 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | 2,67 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | 2,60 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | 2,54 |
Приложение Б
(справочное)
Таблица Б 1 - Критические значения t-критерия Стьюдента для уровней значимости 0,05 и 0,01 (tт)
| Число степеней свободы k | α | Число степеней свободы k | α | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| 12,71 | 63,66 | 2,10 | 2,88 | ||
| 4,30 | 9,92 | 2,09 | 2,86 | ||
| 3,18 | 5,48 | 2,08 | 2,85 | ||
| 2,78 | 4,60 | 2,08 | 2,83 | ||
| 2,57 | 4,03 | 2,07 | 2,82 | ||
| 2,45 | 3,71 | 2,07 | 2,81 | ||
| 2,36 | 3,50 | 2,06 | 2,80 | ||
| 2,31 | 3,36 | 2,06 | 2,78 | ||
| 2,26 | 3,25 | 2,06 | 2,78 | ||
| 2,23 | 3,17 | 2,05 | 2,77 | ||
| 2,20 | 3,11 | 2,05 | 2,76 | ||
| 2,18 | 3,05 | 2,05 | 2,76 | ||
| 2,16 | 3,01 | 2,04 | 2,75 | ||
| 2,14 | 2,98 | 2,02 | 2,70 | ||
| 2,13 | 2,95 | 2,00 | 2,66 | ||
| 2,12 | 2,92 | 1,98 | 2,62 | ||
| 2,11 | 2,90 | ∞ | 1,96 | 2,58 |
